Binomialverteilung
Die Binomialverteilung ist die Wahrscheinlichkeitsverteilung für eine Bernoulli-Kette.
Bernoulli-Experiment
Ein Zufallsexperiment mit nur zwei Ergebnissen, Erfolg und Misserfolg, heißt Bernoulli-Experiment. Die Wahrscheinlichkeit für Erfolg wird mit [math]\displaystyle{ p }[/math] und die Wahrscheinlichkeit für Misserfolg mit [math]\displaystyle{ q=1-p }[/math] bezeichnet. Dabei gilt [math]\displaystyle{ p \in \mathbb{R} }[/math] und [math]\displaystyle{ 0 \leq p \leq 1 }[/math].
Bernoulli-Kette
Ein Zufallsexperiment, das aus [math]\displaystyle{ n\in\mathbb{N} }[/math] unabhängigen Durchführungen desselben Bernoulli-Experiments besteht, heißt Bernoulli-Kette der Länge [math]\displaystyle{ n }[/math].
Definition
Gegeben ist eine Bernoulli-Kette der Länge [math]\displaystyle{ n \in \mathbb{N} }[/math]. Für jedes Bernoulli-Experiment ist die Erfolgswahrscheinlichkeit [math]\displaystyle{ p }[/math] mit [math]\displaystyle{ p \in \mathbb{R} }[/math] und [math]\displaystyle{ 0 \leq p \leq 1 }[/math]. Die Zufallsvariable [math]\displaystyle{ X }[/math] gibt die Anzahl der Erfolge an. Dann beträgt die Wahrscheinlichkeit für genau [math]\displaystyle{ k }[/math] Erfolge [math]\displaystyle{ P(X=k)=\binom{n}{k}\cdot p^k\cdot(1-p)^{(n-k)} }[/math] mit [math]\displaystyle{ 0 \leq k \leq n }[/math] und [math]\displaystyle{ n\in\mathbb{N} }[/math]. [math]\displaystyle{ P:\mathbb{N}_0^{\leq n} \rightarrow \mathbb{R} }[/math] heißt dann Binomialverteilung mit den Parametern [math]\displaystyle{ n }[/math] und [math]\displaystyle{ p }[/math]. Für [math]\displaystyle{ P(X=k) }[/math] schreibt man auch [math]\displaystyle{ B_{n;p}(k) }[/math] oder [math]\displaystyle{ B(n;p;k) }[/math] und nennt [math]\displaystyle{ X }[/math] eine [math]\displaystyle{ B_{n;p} }[/math]-verteilte Zufallsvariable. [math]\displaystyle{ \binom{n}{k} }[/math] ist der Binomialkoeffizient.
Eigenschaften
Erwartungswert
Es sei [math]\displaystyle{ X }[/math] eine [math]\displaystyle{ B_{n;p} }[/math]-verteilte Zufallsvariable mit [math]\displaystyle{ n \in \mathbb{N} }[/math], [math]\displaystyle{ p }[/math] mit [math]\displaystyle{ p \in \mathbb{R} }[/math] und [math]\displaystyle{ 0 \leq p \leq 1 }[/math], dann ist [math]\displaystyle{ \mu=E(X)=n\cdot p }[/math] der Erwartungswert [math]\displaystyle{ X }[/math].
Varianz
Es sei [math]\displaystyle{ X }[/math] eine [math]\displaystyle{ B_{n;p} }[/math]-verteilte Zufallsvariable mit [math]\displaystyle{ n \in \mathbb{N} }[/math], [math]\displaystyle{ p }[/math] mit [math]\displaystyle{ p \in \mathbb{R} }[/math] und [math]\displaystyle{ 0 \leq p \leq 1 }[/math], dann ist [math]\displaystyle{ \sigma^2=V(X)=n\cdot p\cdot(1-p) }[/math] die Varianz von [math]\displaystyle{ X }[/math].
Standardabweichung
Es sei [math]\displaystyle{ X }[/math] eine [math]\displaystyle{ B_{n;p} }[/math]-verteilte Zufallsvariable mit [math]\displaystyle{ n \in \mathbb{N} }[/math], [math]\displaystyle{ p }[/math] mit [math]\displaystyle{ p \in \mathbb{R} }[/math] und [math]\displaystyle{ 0 \leq p \leq 1 }[/math], dann ist [math]\displaystyle{ \sigma=\sqrt{V\left(X\right)}=\sqrt{n\cdot p\cdot\left(1-p\right)} }[/math] die Standardabweichung von [math]\displaystyle{ X }[/math].
Histogramm
Im folgenden Video wird das Histogramm der Binomialverteilung erläutert.
Sigmaregeln
Es sei [math]\displaystyle{ X }[/math] eine [math]\displaystyle{ B_{n;p} }[/math]-verteilte Zufallsvariable mit [math]\displaystyle{ n \in \mathbb{N} }[/math], [math]\displaystyle{ p }[/math] mit [math]\displaystyle{ p \in \mathbb{R} }[/math] und [math]\displaystyle{ 0 \leq p \leq 1 }[/math], dann gilt
- [math]\displaystyle{ P\left(\mu-\sigma\leq X\leq \mu+\sigma\right)\approx0,683 }[/math] [math]\displaystyle{ 1\sigma }[/math]-Regel
- [math]\displaystyle{ P\left(\mu-2\sigma\leq X\leq \mu+2\sigma\right)\approx0,955 }[/math] [math]\displaystyle{ 2\sigma }[/math]-Regel
- [math]\displaystyle{ P\left(\mu-3\sigma\leq X\leq\mu+3\sigma\right)\approx0,997 }[/math] [math]\displaystyle{ 3\sigma }[/math]-Regel mit [math]\displaystyle{ \sigma \geq 3 }[/math]
- [math]\displaystyle{ P\left(\mu-1,64\sigma\leq X\leq\mu+1,64\sigma\right)\approx0,9 }[/math] 90%-Regel
- [math]\displaystyle{ P\left(\mu-1,96\sigma\leq X\leq\mu+1,96\sigma\right)\approx0,95 }[/math] 95%-Regel
- [math]\displaystyle{ P\left(\mu-2,58\sigma\leq X\leq\mu+2,58\sigma\right)\approx0,99 }[/math] 99%-Regel
Diese Regeln können im Histogramm grafisch dargestellt werden.
Regeln zum Umformen von Wahrscheinlichkeiten
Um Wahrscheinlichkeiten für eine [math]\displaystyle{ B_{n;p} }[/math]-verteilte Zufallsvariable [math]\displaystyle{ X }[/math] mit dem Taschenrechner zu berechnen, müssen die Wahrscheinlichkeiten gemäß den folgenden Regeln umgeformt werden. Dabei gilt [math]\displaystyle{ k_1,~k_2 \in \mathbb{N} }[/math]. (Siehe auch Größer-Kleiner-Zeichen):
- [math]\displaystyle{ P(X= k_1) }[/math] kann mit dem Taschenrechner direkt berechnet werden
- [math]\displaystyle{ P(X\leq k_1) }[/math] kann mit dem Taschenrechner direkt berechnet werden
- [math]\displaystyle{ P(X\lt k_1)=P(X\leq (k_1-1)) }[/math]
- [math]\displaystyle{ P(X\gt k_1)=1-P(X\leq k_1) }[/math]
- [math]\displaystyle{ P(X\geq k_1)=1-P(X\lt k_1)=1-P(X\leq (k_1-1)) }[/math]
- [math]\displaystyle{ P(k_1 \leq X \leq k_2)=P(X\leq k_2)-P(X\leq (k_1-1)) }[/math]
- [math]\displaystyle{ P(k_1 \lt X \lt k_2)=P((k_1+1) \leq X \leq (k_2-1))=P(X\leq (k_2-1))-P(X\leq k_1) }[/math]
Auslastungmodell
Mittels der Formel [math]\displaystyle{ P(X=k) = {n \choose k}\cdot\left(\frac{m}{60}\right)^k\cdot\left(1-\frac{m}{60}\right)^{n-k} }[/math] lässt sich die Wahrscheinlichkeit dafür errechnen, dass [math]\displaystyle{ k \in \mathbb{N} }[/math] von [math]\displaystyle{ n\in \mathbb{N} }[/math] Personen eine Tätigkeit, die durchschnittlich [math]\displaystyle{ m \in \mathbb{R}^{\geq 0} }[/math] Minuten pro Stunde dauert, gleichzeitig ausführen.
Beispiele
Bernoulli-Experiment einfacher Münzwurf
Das Zufallsexperiment des einfachen Münzwurfes mit Zahl (Erfolg) oder Kopf (Misserfolg) als Ergebnis ist ein Bernoulli-Experiment. Für die Erfolgswahrscheinlichkeit gilt [math]\displaystyle{ p=\frac{1}{2} }[/math] (Zahl) und für die Misserfolgswahrscheinlichkeit gilt [math]\displaystyle{ q=1-\frac{1}{2}=\frac{1}{2} }[/math] (Kopf).
Bernoulli-Kette zweifacher Münzwurf
Der zweifache Münzwurf ist ein Beispiel für eine Bernoulli-Kette, da die Durchführungen unabhängig voneinander sind. D. h. bei jedem Münzwurf bleibt die Wahrscheinlichkeit für Zahl [math]\displaystyle{ p=\frac{1}{2} }[/math] und für Kopf [math]\displaystyle{ q=\frac{1}{2} }[/math].
Binomialverteilung beim 20-maligen Werfen eines Würfels
Wir betrachten die Bernoulli-Kette 20-maliges werfen eines Würfels. Eine 6 zu würfeln bedeutet Erfolg und jede andere Zahl bedeutet Misserfolg. Das einmalige Werfen des Würfels ist ein Bernoulli-Experiment mit der Erfolgswahrscheinlichkeit [math]\displaystyle{ p=\frac{1}{6} }[/math] und der Misserfolgswahrscheinlichkeit [math]\displaystyle{ q=\frac{5}{6} }[/math]. Damit ist [math]\displaystyle{ X }[/math], Häufigkeit der Augenzahl 6, eine [math]\displaystyle{ B_{20;\frac{1}{6}} }[/math]-verteilte Zufallsvariable. Die Wahrscheinlichkeit, beim 20-maligen Werfen eines Würfels genau 3-mal die 6 zu würfeln, beträgt [math]\displaystyle{ P(X=3)=\binom{20}{3}\cdot{\frac{1}{6}}^3\cdot(1-\frac{1}{6})^{(20-3)}=\binom{20}{3}\cdot{\frac{1}{6}}^3\cdot{\frac{5}{6}}^{17}\approx0,238 }[/math].
Binomialverteilung beim dreifachen Münzwurf
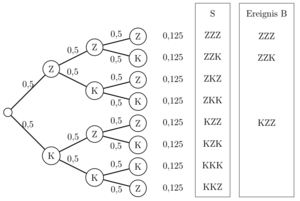
Eine Münze wird dreimal geworfen und man beobachtet, in welcher Reihenfolge Zahl (Z) und Kopf (K) oben liegen. Die Ergebnismenge ist [math]\displaystyle{ S = \{ZZZ; ZZK; ZKZ; ZKK; KZZ; KZK; KKZ; KKK\} }[/math]. Da ein Laplace-Experiment vorliegt, beträgt die Wahrscheinlichkeit genau zweimal Kopf zu werfen [math]\displaystyle{ P(E)=\frac{3}{8}=0,375 }[/math] mit [math]\displaystyle{ E=\{KKZ;KZK;ZKK\} }[/math]. Wir wenden die Binomialverteilung wie folgt an:
Wir betrachten die [math]\displaystyle{ B_{3;\frac{1}{2}} }[/math]-verteilte Zufallsvariable [math]\displaystyle{ X }[/math], die die Häufigkeit von Kopf angibt, und wollen [math]\displaystyle{ P(X=2) }[/math] bestimmen. Jeder Pfad der Bernoulli-Kette besteht aus insgesamt 3 Teilpfade, wovon genau 2 Teilpfade zu Kopf führen müssen. Da die Reihenfolge der Teilpfade keine Rolle spielen und ein Teilpfad nicht doppelt vorkommen darf, gibt es insgesamt [math]\displaystyle{ \binom{3}{2}=3 }[/math] mögliche Pfade (Siehe: Ohne Beachtung der Reihenfolge, Ohne Zurücklegen). Für jeden Pfad gilt: Zwei Teilpfade besitzen jeweils die Wahrscheinlichkeit [math]\displaystyle{ \frac{1}{2} }[/math] für Kopf und ein Teilpfad besitzt die Wahrscheinlichkeit [math]\displaystyle{ \frac{1}{2} }[/math] für Zahl. Es gilt also:
[math]\displaystyle{ P(X=2)=\binom{3}{2}\cdot{\frac{1}{2}}^2\cdot(1-\frac{1}{2})^{(3-2)}=3\cdot{\frac{1}{2}}^2\cdot{\frac{1}{2}}^1=3\cdot0,125=0,375 }[/math]
[math]\displaystyle{ \binom{3}{2} }[/math] ist gleichbedeutend mit „wir erhalten genau zwei Erfolge (Kopf) aus insgesamt 3 Würfen“. [math]\displaystyle{ (\frac{1}{2})^2 }[/math] ist die Wahrscheinlichkeit für zweimal Erfolg (Kopf) und [math]\displaystyle{ (\frac{1}{2})^1 }[/math] ist die Wahrscheinlichkeit für einmal Misserfolg (Zahl).
Erwartungswert, Varianz, Standardabweichung und 95% Regeln anwenden
Im Alter zwischen 15 und 20 Jahren rauchen 25,5% der deutschen Bevölkerung. In einer Schule mit 640 Schülerinnen und Schülern in diesem Alter rauchen 118 Schülerinnen und Schüler.
Betrachten wir die Zufallsvariable [math]\displaystyle{ X }[/math], Anzahl rauchende 15-20-Jährige in der Schule, dann liegt eine Bernoulli-Kette mit [math]\displaystyle{ n=640 }[/math] und [math]\displaystyle{ p=0,255 }[/math] vor. Der Erwartungswert beträgt [math]\displaystyle{ \mu=E(X)=640 \cdot 0,255=163,2 }[/math] und die Varianz ist [math]\displaystyle{ \sigma^2=V(X)=640\cdot0,255\cdot0,745=121,584 }[/math]. Die Standardabweichung ist also [math]\displaystyle{ \sigma\approx\ 11 }[/math]. Die Anzahl der rauchenden Schülerinnen und Schülern der Schule liegt mit 118 unter der erwarteten Anzahl von ungefähr [math]\displaystyle{ \mu=163 }[/math] und sogar unter [math]\displaystyle{ 163-11=152 }[/math], wenn die erwartete Abweichung von [math]\displaystyle{ \sigma \approx 11 }[/math] berücksichtigt wird.
Wir setzen diese Werte in die Gleichung für die 95%-Regel ein und erhalten
[math]\displaystyle{ P\left(163,2-1,96\cdot11,03\leq X\le163+1,96\cdot11,03\right)\approx0,95 }[/math]
[math]\displaystyle{ P\left(141,6\le X\le184,8\right)\approx0,95 }[/math]
Legen wir zugrunde, dass ein Schüler oder eine Schülerin mit einer Wahrscheinlichkeit von 25,5% Raucher oder Raucherin ist, dann sind mit einer Wahrscheinlichkeit von 95% zwischen 142 und 184 Raucherinnen und Raucher an der Schule.