Gewinnfunktion

Mit Hilfe einer Gewinnfunktion wird der Gewinn für eine bestimmte Produktionsmenge ermittelt. Der Gewinn berechnet sich durch Erlös minus Kosten.

Definition

Eine Funktion $G:{\mathbb{D}}_{ök}\to {\mathbb{W}}_G$, die jeder Produktionsmenge $x$ den Gewinn $G(x)$ zuordnet, heißt Gewinnfunktion. Dabei ist $x\in {\mathbb{D}}_{\text{ök}}=[0;x_{max}]$, wobei ${\mathbb{D}}_{\text{ök}}$ der ökonomische Definitionsbereich und $x_{max}\in \mathbb{R}$ die Kapazitätsgrenze ist. $x$ ist häufig in ME (Mengeneinheiten) und $G(x)$ in GE (Geldeinheiten) gegeben. Die Gewinnfunktion ist die Differenz aus der Erlösfunktion und der Kostenfunktion: $G(x)=E(x)-K(x)$

Gewinnschwelle, Gewinngrenze und Gewinnzone

Es sei $G:{\mathbb{D}}_{ök}\to {\mathbb{W}}_G$ eine Gewinnfunktion. Die Gewinnschwelle $x_s\in {\mathbb{D}}_{\text{ök}}$ ist die kleinste Produktionsmenge, für die der Gewinn gleich 0 ist. Die Gewinngrenze $x_g\in {\mathbb{D}}_{\text{ök}}$ ist die größte Produktionsmenge, für die der Gewinn gleich 0 ist. In der Gewinnzone, $[x_s;x_g]$, liegen die Produktionsmengen, für die der Gewinn nicht negativ ist. Die Gewinnschwelle und die Gewinngrenze werden durch $K(x)=E(x)$ oder $G\left(x\right)=E\left(x\right)-K(x)=0$ berechnet. Sie sind also Nullstellen der Gewinnfunktion.

Break-Even-Point (BEP) für lineare Funktionen

Für eine lineare Gewinnfunktion $G:{\mathbb{D}}_{ök}\to {\mathbb{W}}_G$ mit der Gewinnschwelle $x_s\in {\mathbb{D}}_{\text{ök}}$ heißt der Punkt $BEP(x_s|E(x_s))$ Break-Even-Point.

Gewinnmaximum

Es sei $G:{\mathbb{D}}_{ök}\to {\mathbb{W}}_G$ eine Gewinnfunktion. Das globale Maximum $G(x_0)$ von $G$ heißt Gewinnmaximum. Die dazugehörige Maximalstelle $x_0\in {\mathbb{D}}_{ök}$ heißt gewinnmaximale Ausbringungsmenge.

Beispiele

Eine lineare Gewinnfunktion herleiten und analysieren

Die Produktion von Fahrrädern verursacht fixe Kosten von 2700 €. Die variablen Stückkosten betragen 30 € pro Fahrrad. Die produzierten Fahrräder werden für jeweils 300 € pro Stück verkauft. Die Kapazitätsgrenze beträgt 40 Stück. Wir analysieren im Folgenden die Gewinnsituation.

Gewinnfunktion herleiten

Für die Kostenfunktion gilt $K(x)=30x+2700$ mit $K_v=30$ und $K_f=2700$. Weil der Erlös pro Einheit 300 € beträgt, ist $E_v(x)=300$ und die Erlösfunktion ist $E(x)=300x$. Die Gewinnfunktion wird durch $G(x)=E(x)-K(x)=300x-(30x+2700)=270x-2700$ berechnet.

Gewinn berechnen

Der Gewinn für die Kapazitätsgrenze beträgt $G(40)=282\cdot 40-2700=8100$ €.

Gewinnschwelle berechnen

Wegen

$G(x)=0$

$270x-2700=0|+2700$

$270x=2700|:270$

$x=10$

beträgt die Gewinnschwelle $x_s=10$ Fahrräder. Alternativ können wir die Erlösfunktion und die Kostenfunktion gleichsetzen um die Gewinnschwelle zu berechnen:

$E(x)=K(x)$

$300x=30x+2700|-30x$

$300x-30x=2700$

$270x=2700|:270$

$x=10$

Break-Even-Point berechnen

Außerdem gilt $E(10)=300\cdot 10=3000$. Der Break-Even-Point ist damit $BEP(10|3000)$. Werden 10 ME produziert, sind die Kosten und der Erlös gleich hoch und betragen jeweils 3000 €.

Eine ganzrationale Gewinnfunktion dritten Grades herleiten und analysieren

Die variable Kostenfunktion für ein Produkt ist durch $K_v(x)=0,2x^3-4x^2+30x$ gegeben. Die Fixkosten betragen 20 GE. Der Verkaufspreis pro Stück beträgt 32,8 GE.

Gewinnfunktion herleiten

Die Erlösfunktion, die Kostenfunktion und die Gewinnfunktion berechnen sich wie folgt:

$E(x)=32,8x$

$K(x)=K_v(x)+K_f=,2x^3-4x^2+30x+20$

$G(x)=E(x)-K(x)=32,8x-(0,2x^3-4x^2+30x+20)=32,8x-0,2x^3+4x^2-30x-20=-0,2x^3+4x^2+2,8x-20$

Gewinnschwelle, Gewinngrenze und Gewinnzone berechnen

Graph der Gewinnfunktion $G(x)=-0,2x^3+4x^2-30x-20$

Die Gewinnfunktion für ein Produkt ist durch $G(x)=-0,2x^3+4x^2+2,8x-20$ gegeben. x ist die Menge in ME und G(x) gibt den Gewinn in GE an.

Wir ermitteln Gewinnschwelle, Gewinngrenze und Gewinnzone, indem wir die Nullstellen mit dem Taschenrechner berechnen:

$0=-0,2x^3+4x^2+2,8x-20$

$x_1\approx -2,45,x_2=2,x_3\approx 20,45$ Die Gewinnschwelle beträgt 2 ME, die Gewinngrenze 20,45 ME, die Gewinnzone beträgt $[2;20,45]$ und der ökonomische Definitionsbereich beträgt ${\mathbb{D}}_{\text{ök}}=[0;20,45]$, da keine Kapazitätsgrenze gegeben ist.

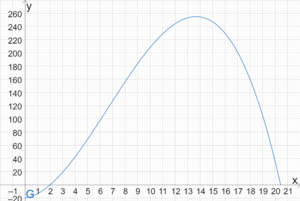
Graph der Gewinnfunktion zeichnen

Um den Graphen der Gewinnfunktion zu zeichnen, erstellen wir eine Wertetabelle für x-Werte in ${\mathbb{D}}_{\text{ök}}$:

$x$	0	2	4	6	8	10	12	14	16	18	20	22
$G(x)$	-20	0	42,4	97,6	156	208	244	254,4	229,6	160	36	-160

Beispielsweise gilt $G(4)=-0,2\cdot 2^3+4\cdot 2^2+2,8\cdot 2-20=42,4$. Wir zeichnen die Punkte dann in ein Koordinatensystem ein, verbinden diese und erhalten den Graph auf der rechten Seite. Wir erkennen, dass die gewinnmaximale Ausbringungsmenge ca. 13,67 ME und das Gewinnmaximum ca. 253 GE beträgt. Der dazugehörige Hochpunkt ist $G_{max}(13,67|253)$.

Gewinnmaximale Ausbringungsmenge und Gewinnmaximum ermitteln

Das Gewinnmaximum und die gewinnmaximale Ausbringungsmenge berechnen sich für $G(x)=-0,2x^3+4x^2+2,8x-20$ mit $G^{\prime }(x)=-0,6x^2+8x+2,8$ und $G^{″}(x)=-1,2x+8$ wie folgt:

1. Notwendige Bedingung:
   $G^{\prime }(x)=0$
   $-0,6x^2+8x+2,8=0|$ Lösen mit Taschenrechner
   $x\approx -0,34\notin {\mathbb{D}}_{ök}$ oder $x\approx 13,67\in {\mathbb{D}}_{ök}$
2. Hinreichende Bedingung:
   $G^{″}(13,67)=-1,2\cdot 13,67+8\approx -8,4<0$
   Bei $x\approx 13,67$ liegt ein Maximum vor.
3. Extremwert berechnen:
   $G(13,67)=-0,2\cdot 13,{67}^3+4\cdot 13,{67}^2+2,8\cdot 13,67-20\approx 253$
   Das Gewinnmaximum beträgt ca. 253 GE und die gewinnmaximale Ausbringungsmenge beträgt ca. 13,67 ME.