Graph
Der Graph einer Funktion [math]\displaystyle{ f }[/math] ist die Menge aller Punkte [math]\displaystyle{ (x|f(x)) }[/math] wobei die Variable [math]\displaystyle{ x }[/math] Werte aus dem Definitionsbereich annimmt und [math]\displaystyle{ f(x) }[/math] die dazugehörigen Funktionswerte sind. Wir veranschaulichen diese Menge graphisch in einem Koordinatensystem, indem die Punkte eingezeichnet und verbunden werden.
Definition
Der Graph oder Funktionsgraph einer Funktion [math]\displaystyle{ f: \mathbb{D} \rightarrow \mathbb{W} }[/math] ist die Menge [math]\displaystyle{ G_f=\{(x|f(x) \in \mathbb{D} \times \mathbb{W}| x \in \mathbb{D}\} }[/math]. Die graphische Veranschaulichung der Menge bezeichnen wir ebenfalls als Graph.
Beispiele
Graph einer linearen Funktion
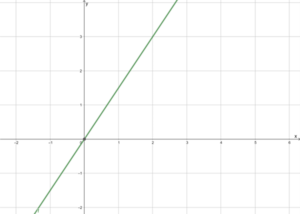
Die Abbildung zeigt den Graph einer linearen Funktion. Die einzelnen Punkte können als Menge oder Wertetabelle dargestellt werden:
[math]\displaystyle{ G_f=\{...;(-2|-3);(-1|-1,5);(0|0);(1|1,5);(2|3);(3|4,5);...\} }[/math]
| [math]\displaystyle{ x }[/math] | ... | -2 | -1 | 0 | 1 | 2 | 3 | ... |
|---|---|---|---|---|---|---|---|---|
| [math]\displaystyle{ f(x) }[/math] | ... | -3 | -1,5 | 0 | 1,5 | 3 | 4,5 | ... |
Um den Graphen von [math]\displaystyle{ f }[/math] zu zeichnen, stellen wir erst die Menge [math]\displaystyle{ G_f }[/math] oder die Wertetabelle auf. Wir wählen [math]\displaystyle{ x }[/math]-Werte gemäß dem Definitionsbereich und berechnen dann die [math]\displaystyle{ y }[/math]-Werte. Anschließend werden die Punkte eingezeichnet.
Graph einer quadratischen Funktion
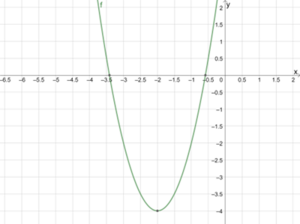
Die Abbildung zeigt den Graph einer quadratischen Funktion. Die einzelnen Punkte können als Menge oder Wertetabelle dargestellt werden:
[math]\displaystyle{ G_f=\{...;(-4|4);(-3|-2);(-2|-4);(-1|-2);(0|4);(1|14);(2|28);...\} }[/math]
| [math]\displaystyle{ x }[/math] | ... | -4 | -3 | -2 | -1 | 0 | 1 | 2 | ... |
|---|---|---|---|---|---|---|---|---|---|
| [math]\displaystyle{ f(x) }[/math] | ... | 4 | -2 | -4 | -2 | 4 | 14 | 28 | ... |