Hauptsatz der Differential- und Integralrechnung

Mit Hilfe des Hauptsatzes der Differential- und Integralrechnung werden Flächeninhalte zwischen dem Graphen einer Funktion der x-Achse berechnet.

Flächeninhaltsfunktion und Stammfunktion

Der Flächeninhalt zwischen dem Graphen einer Funktion [math]\displaystyle{ f }[/math] und der x-Achse im Intervall [math]\displaystyle{ [0;x] }[/math] wird durch den Funktionswert einer Flächeninhaltsfunktion [math]\displaystyle{ A }[/math] ermittelt.

Es sei [math]\displaystyle{ F }[/math] die Stammfunktion zu einer ganzrationalen Funktion [math]\displaystyle{ f }[/math] mit der Konstanten [math]\displaystyle{ C=0 }[/math], dann ist [math]\displaystyle{ F }[/math] die Flächeninhaltsfunktion zu [math]\displaystyle{ f }[/math].

Bestimmtes Integral

Das bestimmte Integral einer stetigen Funktion [math]\displaystyle{ f }[/math] auf dem Intervall [math]\displaystyle{ [a; b] }[/math] ist durch

[math]\displaystyle{ \int_a^b f(x) \, dx }[/math]

gegeben.

Für auf den Intervallen [math]\displaystyle{ [a;b] \subseteq [a;c] }[/math] und [math]\displaystyle{ [b;c] \subseteq [a;c] }[/math] stetige Funktionen [math]\displaystyle{ f, ~g }[/math] gelten die folgenden Rechenregeln:

Faktorregel

[math]\displaystyle{ \int_a^b c \cdot f(x) \, dx=c \cdot \int_a^b f(x) \, dx }[/math]

Summenregel

[math]\displaystyle{ \int_a^b (f(x)+g(x)) \, dx = \int_a^b f(x) \, dx + \int_a^bg(x) \, dx }[/math]

Intervalladditivität

[math]\displaystyle{ \int_a^c f(x) \, dx=\int_a^b f(x) \, dx+\int_b^c f(x) \, dx }[/math]

Vertauschen der Integrationsgrenzen

[math]\displaystyle{ \int_a^b f(x) \, dx=-\int_b^a f(x) \, dx }[/math]

Definition

Falls [math]\displaystyle{ F }[/math] eine Stammfunktion von [math]\displaystyle{ f }[/math] ist, so wird das bestimmte Integral von [math]\displaystyle{ f }[/math] auf dem Intervall [math]\displaystyle{ [a;b] }[/math] durch die Gleichung

[math]\displaystyle{ \int_a^b f(x) \, dx = F(b) - F(a) }[/math]

berechnet.

Hierbei bezeichnet [math]\displaystyle{ a }[/math] die untere und [math]\displaystyle{ b }[/math] die obere Grenze des Integrals. Das bestimmte Integral gibt den orientierten Flächeninhalt an, das heißt:

• Liegt der Graph von [math]\displaystyle{ f }[/math] oberhalb der x-Achse, ist das bestimmte Integral positiv.
• Liegt der Graph von [math]\displaystyle{ f }[/math] unterhalb der x-Achse, ist das bestimmte Integral negativ.
• Liegt der Graph von [math]\displaystyle{ f }[/math] sowohl unterhalb als auch oberhalb der x-Achse, ist das bestimmte Integral die Differenz aus dem oberen Flächeninhalt und dem unteren Flächeninhalt.

Integralfunktion

Es sei [math]\displaystyle{ f }[/math] eine auf dem Intervall [math]\displaystyle{ [a;b] }[/math] stetige Funktion, dann ist

[math]\displaystyle{ I_a(x)=\int_a^x f(t) \, dt }[/math]

die dazugehörige Integralfunktion.

Flächen zwischen Funktionsgraphen ermitteln

Es seien [math]\displaystyle{ f, ~g }[/math] auf dem Intervall [math]\displaystyle{ [a;b] }[/math] stetige Funktionen. Die Fläche zwischen den Graphen von [math]\displaystyle{ f, ~g }[/math] wird wie folgt ermittelt:

1. Schnittstellen [math]\displaystyle{ x_{S_1},\dots,x_{S_n} }[/math] mit [math]\displaystyle{ n \in \mathbb{N} }[/math] der Graphen von [math]\displaystyle{ f, ~g }[/math] ermitteln.
2. Stammfunktionen [math]\displaystyle{ F,~G }[/math] ermitteln
3. [math]\displaystyle{ A=|\int_{x_{S_1}}^{x_{S_2}}(f(x)-g(x)) \, dx|+|\int_{x_{S_2}}^{x_{S_3}}(f(x)-g(x)) \, dx|+\dots+|\int_{x_{S_{n-1}}}^{x_{S_n}}(f(x)-g(x)) \, dx| }[/math] berechnen. (siehe Betragsfunktion)

Beispiele

Flächeninhalt ermitteln

Das bestimmte Integral der Funktion [math]\displaystyle{ f(x)=x^2 }[/math] auf dem Intervall [math]\displaystyle{ [1;2] }[/math] berechnet sich durch [math]\displaystyle{ \int_1^2 x^2 \, dx=\frac{7}{3} }[/math].

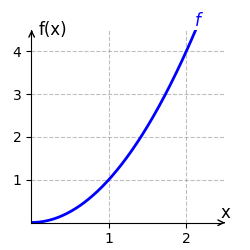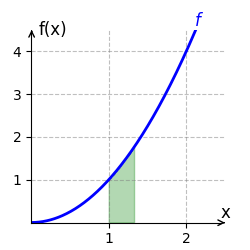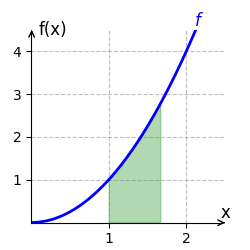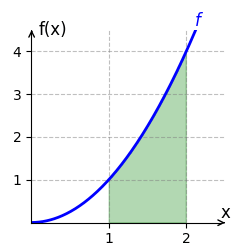
Wir berechnen das bestimmte Integral von [math]\displaystyle{ f(x) = x^2 }[/math] auf dem Intervall [math]\displaystyle{ [1;2] }[/math]. Eine Stammfunktion von [math]\displaystyle{ f }[/math] ist [math]\displaystyle{ F(x) = \frac{x^3}{3} }[/math]. Das bestimmte Integral auf dem Intervall [1;2] wird durch

[math]\displaystyle{ \int_1^2 x^2 \, dx = F(2) - F(1) }[/math]

[math]\displaystyle{ = \frac{2^3}{3} - \frac{1^3}{3} = \frac{8}{3} - \frac{1}{3} = \frac{7}{3} }[/math]

berechnet. Der Graph von [math]\displaystyle{ f }[/math] verläuft auf dem Intervall [math]\displaystyle{ [1;2] }[/math] oberhalb der x-Achse. Der Flächeninhalt beträgt somit [math]\displaystyle{ \frac{7}{3} }[/math] Einheiten und ist im rechten Bild grün eingezeichnet.

Wir berechnen den Flächeninhalt zwischen dem Graphen von \(f(t)=\frac{t^5}{24}-\frac{t^3}{2}+t\) und der x-Achse auf dem Intervall [math]\displaystyle{ [-2;2] }[/math] (siehe Graph von [math]\displaystyle{ f }[/math]).

1. Nullstellen von [math]\displaystyle{ f }[/math] berechnen

[math]\displaystyle{ \frac{t^5}{24}-\frac{t^3}{2}+t=0 }[/math]

[math]\displaystyle{ t \approx -3,08 \lor t \approx -1,59 \lor t \approx 0 \lor t \approx 1,59 \lor t \approx 3,08 }[/math]

[math]\displaystyle{ -1,59; 0; 1,59 \in [-2;2] }[/math]

2. Flächeninhalt ermitteln

[math]\displaystyle{ A=|\int_{-2}^{-1,59} f(t) \, dt|+|\int_{-1,59}^{0} f(t) \, dt|+|\int_{0}^{1,59} f(t) \, dt|+|\int_{1,59}^{2} f(t) \, dt| }[/math]

[math]\displaystyle{ \approx |0,13|+|-0,58|+|0,58|+|-0,13| = 0,13+0,58+0,58+0,13= 1,42 }[/math]

Der gesuchte Flächeninhalt beträgt [math]\displaystyle{ A=1,42 }[/math]. Der orientierte Flächeninhalt auf dem Intervall [math]\displaystyle{ [-2;2] }[/math] beträgt [math]\displaystyle{ \int_{-2}^{2} f(t) \, dt=0 }[/math].

Orientierten Flächeninhalt ermitteln

Das bestimmte Integral der Funktion [math]\displaystyle{ f(x)=x }[/math] auf dem Intervall [math]\displaystyle{ [-1;1] }[/math] berechnet sich durch [math]\displaystyle{ \int_{-1}^1 x \, dx= }[/math][math]\displaystyle{ \frac{1}{2} }[/math][math]\displaystyle{ - }[/math][math]\displaystyle{ \frac{1}{2} }[/math][math]\displaystyle{ =0 }[/math].

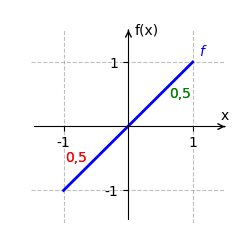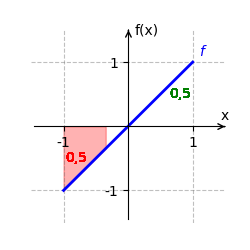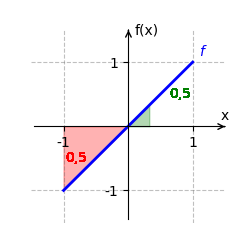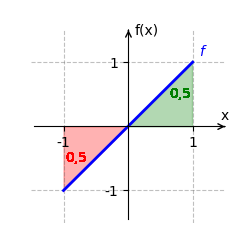
Wir betrachten [math]\displaystyle{ f(x) = x }[/math] auf dem Intervall [math]\displaystyle{ [-1;1] }[/math]. Eine Stammfunktion von [math]\displaystyle{ f }[/math] ist [math]\displaystyle{ F(x) = \frac{x^2}{2} }[/math]. Das bestimmte Integral ist:

[math]\displaystyle{ \int_{-1}^1 x \, dx = F(1) - F(-1) }[/math]

[math]\displaystyle{ = \frac{1^2}{2} - \frac{(-1)^2}{2} = \frac{1}{2} - \frac{1}{2} = 0 }[/math].

Der orientierte Flächeninhalt beträgt [math]\displaystyle{ 0 }[/math], da sich die positiven und negativen Flächeninhalte genau ausgleichen.

Integralfunktion ermitteln

Gegeben sei [math]\displaystyle{ f(x) = 3x }[/math] und [math]\displaystyle{ a = 0 }[/math]. Die Integralfunktion ist:

[math]\displaystyle{ I_0(x) = \int_0^x 3t \, dt }[/math].

Eine Stammfunktion von [math]\displaystyle{ 3t }[/math] ist [math]\displaystyle{ \frac{3t^2}{2} }[/math], also gilt

[math]\displaystyle{ I_0(x) = \frac{3x^2}{2} - \frac{3 \cdot 0^2}{2} = \frac{3x^2}{2} }[/math].

Flächeninhalt zwischen den Graphen von zwei Funktionen ermitteln

Fläche zwischen den Graphen von zwei Funktionen ermitteln

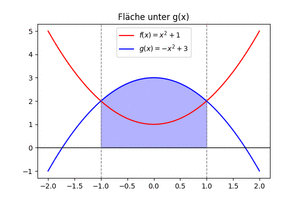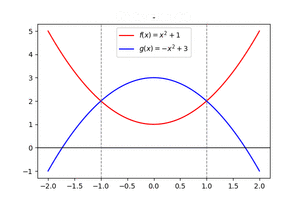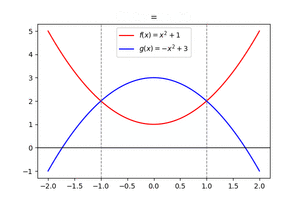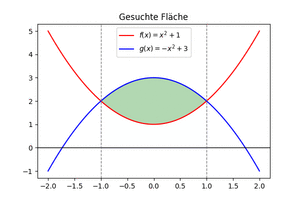
Wir betrachten die Funktionen [math]\displaystyle{ f(x)=x^2+1 }[/math] und [math]\displaystyle{ g(x)=-x^2+3 }[/math] und ermitteln die Fläche zwischen den Graphen der Funktionen.

1. Schnittstellen von [math]\displaystyle{ g,~f }[/math] ermitteln

[math]\displaystyle{ f(x)=g(x) }[/math]

[math]\displaystyle{ x^2+1=-x^2+3 }[/math]

[math]\displaystyle{ 2 \cdot x^2=2 }[/math]

[math]\displaystyle{ x^2=1 }[/math]

[math]\displaystyle{ x=\pm \sqrt{1} }[/math]

[math]\displaystyle{ x=\pm 1 }[/math]

2. Stammfunktionen ermitteln

[math]\displaystyle{ F(x)=\frac{1}{3}x^3+x }[/math]

[math]\displaystyle{ G(x)=-\frac{1}{3}x^3+3x }[/math]

3. Flächeninhalt ermitteln

[math]\displaystyle{ \int_{-1}^{1}(f(x)-g(x)) \, dx=F(1)-G(1)-(F(-1)-G(-1)) }[/math]

[math]\displaystyle{ =\frac{1}{3} \cdot 1^3+1-(-\frac{1}{3}\cdot 1^3+3 \cdot 1) }[/math]

[math]\displaystyle{ -(\frac{1}{3} \cdot (-1)^3+(-1)-(-\frac{1}{3}\cdot (-1)^3+3 \cdot (-1))) }[/math]

[math]\displaystyle{ =-\frac{8}{3} }[/math] (orientierter Flächeninhalt)

Der gesuchte Flächeninhalt ist der Betrag der Zahl und beträgt [math]\displaystyle{ \frac{8}{3} }[/math].