Stetige Funktion

In der Mathematik ist ein stetige Funktion eine Funktion, bei der hinreichend kleine Änderungen des x-Wertes nur beliebig kleine Änderungen des Funktionswertes nach sich ziehen können. Anschaulich bedeutet es, dass der Graph einer stetigen Funktion als eine durchgängige Linie, ohne Sprünge, gezeichnet werden kann.

Definition

Es sei [math]\displaystyle{ f\colon \mathbb{D}_f \to \R }[/math] eine Funktion.

Definition mittels Epsilon-Delta-Kriterium:

[math]\displaystyle{ f }[/math] heißt stetig in [math]\displaystyle{ x_0 \in \mathbb{D}_f }[/math], wenn zu jedem [math]\displaystyle{ \varepsilon\gt 0 }[/math] ein [math]\displaystyle{ \delta \gt 0 }[/math] existiert, so dass für alle [math]\displaystyle{ x \in \mathbb{D}_f }[/math] mit

[math]\displaystyle{ |x - x_0| \lt \delta }[/math]

gilt:

[math]\displaystyle{ |f(x) - f(x_0)| \lt \varepsilon }[/math].

Intuitiv bedeutet die Bedingung der Stetigkeit, dass zu jeder Änderung [math]\displaystyle{ \varepsilon }[/math] des Funktionswertes, die man zu akzeptieren bereit ist, eine maximale Änderung [math]\displaystyle{ \delta }[/math] im Argument gefunden werden kann, die diese Vorgabe sicherstellt.

Definition mittels Grenzwerten:

[math]\displaystyle{ f }[/math] heißt stetig in [math]\displaystyle{ x_0 }[/math], wenn der Grenzwert [math]\displaystyle{ \lim_{x\to x_0} f(x) }[/math] existiert und mit dem Funktionswert [math]\displaystyle{ f(x_0) }[/math] übereinstimmt, wenn also gilt:

[math]\displaystyle{ \lim_{x\to x_0}f(x)=f(x_0) }[/math].

Ist diese Bedingung für ein [math]\displaystyle{ x_0 \in \mathbb{D}_f }[/math] nicht erfüllt, so nennt man [math]\displaystyle{ f }[/math] unstetig in [math]\displaystyle{ x_0 }[/math].

Man spricht von einer stetigen Funktion, wenn die Funktion in jeder Stelle ihres Definitionsbereiches stetig ist.

Beispiele

Unstetige Funktion

Graph der unstetigen Funktion [math]\displaystyle{ f(x)=\begin{cases} x, & \text{wenn }x\le 1\\ x+1, & \text{wenn }x \gt 1 \end{cases} }[/math]

Die Funktion

[math]\displaystyle{ f(x)=\begin{cases} x, & \text{wenn }x\le 1\\ x+1, & \text{wenn }x \gt 1 \end{cases} }[/math]

springt an der Stelle [math]\displaystyle{ x=1 }[/math] vom Funktionswert 1 auf den Funktionswert 2. Am Graph erkennen wir bereits, dass [math]\displaystyle{ f }[/math] in [math]\displaystyle{ x_0=1 }[/math] unstetig ist.

Kontraposition

Wenn die Funktion stetig an [math]\displaystyle{ x_0 = 1 }[/math] wäre, müsste es für jedes [math]\displaystyle{ \epsilon \gt 0 }[/math] ein [math]\displaystyle{ \delta \gt 0 }[/math] geben, sodass [math]\displaystyle{ |f(x) - f(1)| \lt \epsilon }[/math] für alle [math]\displaystyle{ x }[/math] mit [math]\displaystyle{ |x - 1| \lt \delta }[/math] gilt.

Wir wählen nun ein [math]\displaystyle{ \epsilon \lt 1 }[/math]. Wir wählen [math]\displaystyle{ x = 1 + \frac{\delta}{2} }[/math] und erhalten wir [math]\displaystyle{ |f(x) - f(1)| = |1 + \frac{\delta}{2} + 1 - 1| =1 + \frac{\delta}{2} }[/math], was größer als [math]\displaystyle{ \epsilon }[/math] ist, da [math]\displaystyle{ \epsilon \lt 1 }[/math].

Das bedeutet, dass es kein [math]\displaystyle{ \delta \gt 0 }[/math] geben kann, das [math]\displaystyle{ |f(x) - f(1)| \lt \epsilon }[/math] sicherstellt, wenn [math]\displaystyle{ x \gt 1 }[/math].

Fallunterscheidung

Fall 1: [math]\displaystyle{ x \leq 1 }[/math]

Für [math]\displaystyle{ x \leq 1 }[/math] ist [math]\displaystyle{ f(x) = x }[/math]. Wir haben:

[math]\displaystyle{ |f(x) - f(1)| = |x - 1| }[/math]

Da [math]\displaystyle{ |x - 1| \lt \delta }[/math], können wir [math]\displaystyle{ |f(x) - f(1)| \lt \epsilon }[/math] machen, indem wir [math]\displaystyle{ \delta = \epsilon }[/math] wählen. In diesem Fall ist die Bedingung des [math]\displaystyle{ \epsilon }[/math]-[math]\displaystyle{ \delta }[/math]-Kriteriums erfüllt.

Fall 2: [math]\displaystyle{ x \gt 1 }[/math]

Für [math]\displaystyle{ x \gt 1 }[/math] ist [math]\displaystyle{ f(x) = x + 1 }[/math]. Wir haben:

[math]\displaystyle{ |f(x) - f(1)| = |(x + 1) - 1| = |x| }[/math]

Nun setzen wir [math]\displaystyle{ x = 1 + h }[/math] für [math]\displaystyle{ h \gt 0 }[/math] ein:

[math]\displaystyle{ |f(x) - f(1)| = |(1 + h) + 1 - 1| = |1 + h| = 1 + h }[/math]

Da [math]\displaystyle{ h \gt 0 }[/math] ist, ist [math]\displaystyle{ |f(x) - f(1)| = 1 + h }[/math]. Wir können also zeigen, dass für jedes [math]\displaystyle{ \delta }[/math] die Differenz [math]\displaystyle{ |f(x) - f(1)| \geq 1 }[/math] sein kann.

Grenzwertbetrachtung

Grenzwert von links ([math]\displaystyle{ x \to 1^− }[/math])

Für [math]\displaystyle{ x \leq 1 }[/math] ist [math]\displaystyle{ f(x) = x }[/math]. Der Grenzwert von links ist:

[math]\displaystyle{ \lim_{x \to 1^-} f(x) = \lim_{x \to 1^-} x = 1 }[/math]

Grenzwert von rechts ([math]\displaystyle{ x \to 1^+ }[/math]) Für [math]\displaystyle{ x \gt 1 }[/math] ist [math]\displaystyle{ f(x) = x + 1 }[/math]. Der Grenzwert von rechts ist:

[math]\displaystyle{ \lim_{x \to 1^+} f(x) = \lim_{x \to 1^+} (x + 1) = 1 + 1 = 2 }[/math]

Vergleich der Grenzwerte

Für Stetigkeit muss gelten:

[math]\displaystyle{ \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = f(1) }[/math]

Aber in unserem Fall haben wir:

[math]\displaystyle{ \lim_{x \to 1^-} f(x) = 1 \quad \text{und} \quad \lim_{x \to 1^+} f(x) = 2 }[/math]

Da die Grenzwerte von links und von rechts nicht übereinstimmen ([math]\displaystyle{ 1 \neq 2 }[/math]), existiert der Grenzwert [math]\displaystyle{ \lim_{x \to 1} f(x) }[/math] nicht.

Stetige Funktion

Graph der stetigen Funktion [math]\displaystyle{ f(x)=x }[/math]

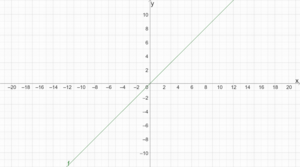
Die Funktion [math]\displaystyle{ f(x) = x }[/math] ist an jeder Stelle [math]\displaystyle{ x_0 \in \mathbb {R} }[/math] stetig. Der Graph ist eine Gerade durch den Ursprung.

Der Funktionswert an einer Stelle [math]\displaystyle{ x_0 }[/math] ist:

[math]\displaystyle{ f(x_0) = x_0 }[/math]

Für [math]\displaystyle{ f(x) = x }[/math] gilt:

[math]\displaystyle{ |f(x) - f(x_0)| = |x - x_0| }[/math]

Da wir wollen, dass [math]\displaystyle{ |f(x) - f(x_0)| \lt \epsilon }[/math] gilt, müssen wir sicherstellen, dass:

[math]\displaystyle{ |x - x_0| \lt \delta \implies |x - x_0| \lt \epsilon }[/math]

Hier sehen wir, dass wir einfach [math]\displaystyle{ \delta = \epsilon }[/math] wählen können. Das bedeutet, dass für jedes [math]\displaystyle{ \epsilon \gt 0 }[/math] ein entsprechendes [math]\displaystyle{ \delta = \epsilon }[/math] existiert, sodass die Bedingung [math]\displaystyle{ |x - x_0| \lt \delta }[/math] garantiert, dass [math]\displaystyle{ |f(x) - f(x_0)| \lt \epsilon }[/math] erfüllt ist.

Da wir für jedes [math]\displaystyle{ \epsilon \gt 0 }[/math] ein [math]\displaystyle{ \delta = \epsilon }[/math] finden können, das die Bedingung des [math]\displaystyle{ \epsilon }[/math]-[math]\displaystyle{ \delta }[/math]-Kriteriums erfüllt, ist die Funktion [math]\displaystyle{ f(x) = x }[/math] an jeder Stelle [math]\displaystyle{ x_0 }[/math] stetig.