Ganzrationale Funktion
Ganzrationale Funktionen haben die Form [math]\displaystyle{ f(x)=a_n \cdot x^n+a_{n-1}x^{n-1}+...+a_1x+a_0 }[/math]. Jede lineare und jede quadratische Funktion ist auch gleichzeitig eine ganzrationale Funktion.
Definition
Ein Term der Form [math]\displaystyle{ a_n \cdot x^n+a_{n-1}x^{n-1}+...+a_1x+a_0 }[/math] mit [math]\displaystyle{ a_n,...,a_0 \in \mathbb{R} }[/math] und [math]\displaystyle{ a_n \neq 0 }[/math] heißt Polynom mit der Variablen [math]\displaystyle{ x }[/math]. Der Exponent [math]\displaystyle{ n }[/math] heißt Grad des Polynoms.
Die Zahlen [math]\displaystyle{ a_n,...,a_0 }[/math] heißen Koeffizienten.
Eine Funktion [math]\displaystyle{ f }[/math], deren Funktionsterm [math]\displaystyle{ f(x) }[/math] als Polynom geschrieben werden kann, heißt ganzrationale Funktion. Der Grad des Polynoms heißt auch Grad der ganzrationalen Funktion.
Beispiele
Eine lineare Funktion der Form [math]\displaystyle{ f(x)=mx+b }[/math] ist eine ganzrationale Funktion. Der Funktionsterm lässt sich auch als [math]\displaystyle{ mx^1+b }[/math] schreiben und ist damit ein Polynom mit dem Grad [math]\displaystyle{ 1 }[/math]. Die Koeffizienten sind [math]\displaystyle{ m, b }[/math].
Die quadratische Funktion [math]\displaystyle{ f(x)=-2x^2+3x+5 }[/math] ist eine ganzrationale Funktion mit Grad [math]\displaystyle{ 2 }[/math] und den Koeffizienten [math]\displaystyle{ -2,3,5 }[/math].
Ganzrationale Funktion 3. Grades
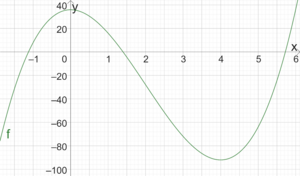
[math]\displaystyle{ f(x)=4x^3-24x^2+36 }[/math] ist eine ganzrationale Funktion, da der Funktionsterm, [math]\displaystyle{ 4x^3-24x^2+36 }[/math], ein Polynom ist. Der Grad von [math]\displaystyle{ f }[/math] ist [math]\displaystyle{ 3 }[/math]. Die Koeffizienten sind [math]\displaystyle{ 3, -2, 0, 36 }[/math]. Der Graph sieht wie folgt aus: