Angebotsfunktion

Die Angebotsfunktion beschreibt die funktionale Beziehung zwischen der Angebot und dem Preis auf einem Markt. Pendant ist die Nachfragefunktion.

Definition

Gegeben sei ein Markt auf dem ein Gut gehandelt wird. Eine Funktion [math]\displaystyle{ p_A:\mathbb{D}_{ök} \rightarrow \mathbb{W}_{p_A} }[/math], die jedem Angebot [math]\displaystyle{ x \in \mathbb{D}_{ök} }[/math] den Preis [math]\displaystyle{ p_A(x) }[/math] in Geldeinheit pro Mengeneinheit zuordnet, heißt Angebotsfunktion. Der Graph der Angebotsfunktion heißt Angebotskurve.

Gesetz des Angebots

Das Gesetz des Angebots besagt, dass das Angebot nach einem Gut steigt, wenn sich der Preis erhöht. Die Angebotskurve verläuft daher von links unten nach rechts oben und ist häufig ein Gerade.

Ökonomischer Definitionsbereich einer Angebotsfunktion

Häufig werden Nachfragefunktion und Angebotsfunktion gemeinsam betrachtet. Für den ökonomischem Definitionsbereich der Angebotsfunktion [math]\displaystyle{ p_A }[/math] gilt dann [math]\displaystyle{ \mathbb{D}_{ök}=[0;x_s] }[/math], wobei [math]\displaystyle{ x_s }[/math] die Sättigungsmenge der dazugehörigen Nachfragefunktion [math]\displaystyle{ p_N }[/math] ist.

Mindestpreis

Es sei [math]\displaystyle{ p_A:\mathbb{D}_{ök} \rightarrow \mathbb{W}_{p_N} }[/math] eine lineare Angebotsfunktion für die das Gesetz des Angebots gilt. Der y-Achsenabschnitt [math]\displaystyle{ p_A(0) }[/math] heißt Mindestpreis. Der Mindestpreis ist der Preis, für den niemand das Gut anbietet.

Beispiele

Angebotskurve einer linearen Angebotsfunktion

Angebotskurve von [math]\displaystyle{ p_A(x)=\frac{2}{3}x+2 }[/math]

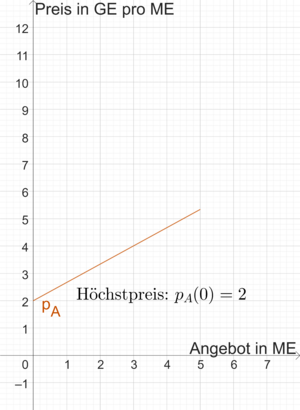
Wir betrachten einen Markt auf dem ein Gut gehandelt wird. Die Angebotsfunktion ist [math]\displaystyle{ p_N(x)=\frac{2}{3}x+2 }[/math]. Die dazugehörige Angebotskurve ist auf der rechten Seite abgebildet. [math]\displaystyle{ x }[/math] ist das Angebot in ME und [math]\displaystyle{ p_A(x) }[/math] ist der dazugehörige Preis des Produkts in GE pro ME. Der Mindestpreis beträgt [math]\displaystyle{ p_A(0)=2 }[/math], da dies der y-Achsenabschnitt ist. Gemäß dem Gesetz des Angebots verläuft die Angebotskurve von links unten nach rechts oben. Beträgt der Preis für das Gut 4 GE pro ME, dann werden insgesamt 3 ME angeboten. Der ökonomische Definitionsbereich ist hier [math]\displaystyle{ \mathbb{D}_{ök}=[0;5] }[/math], da die Sättigungsmenge der dazugehörigen Nachfragefunktion 5 ME beträgt.

Berechnungen mit einer linearen Angebotsfunktion

Wir betrachten wieder [math]\displaystyle{ p_A(x)=\frac{2}{3}x+2 }[/math]. Beträgt das Angebot für für das Gut [math]\displaystyle{ x=3 }[/math] ME, dann muss der Preis für das Gut [math]\displaystyle{ p_A(3)=\frac{2}{3}3+2=4 }[/math] GE pro ME betragen. Beträgt der Preis für das Gut 5 GE pro ME, berechnet sich die Nachfrage in ME durch

[math]\displaystyle{ p_N(x)=\frac{2}{3}x+2 }[/math]
[math]\displaystyle{ 5=\frac{2}{3}x+2~|~-2 }[/math]
[math]\displaystyle{ 3=\frac{2}{3}x~|~:\frac{2}{3} }[/math]
[math]\displaystyle{ 4,5=x }[/math]

Der Mindestpreis in GE pro ME berechnet sich durch [math]\displaystyle{ p_A(0)=\frac{2}{3} \cdot x +2=2 }[/math].