Hauptsatz der Differential- und Integralrechnung: Unterschied zwischen den Versionen
| (200 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
Der Flächeninhalt zwischen dem Graphen einer Funktion <math>f</math> und der x-Achse im Intervall <math>[0;x]</math> wird durch den Funktionswert einer '''Flächeninhaltsfunktion''' <math>A</math> ermittelt. | Der Flächeninhalt zwischen dem Graphen einer Funktion <math>f</math> und der x-Achse im Intervall <math>[0;x]</math> wird durch den Funktionswert einer '''Flächeninhaltsfunktion''' <math>A</math> ermittelt. | ||
Es sei <math>F</math> die [[Stammfunktion]] zu einer Funktion <math>f</math> mit der Konstanten <math>C=0</math>, dann ist <math>F</math> die Flächeninhaltsfunktion zu <math>f</math>. | Es sei <math>F</math> die [[Stammfunktion]] zu einer [[ganzrationale_Funktion|ganzrationalen Funktion]] <math>f</math> mit der Konstanten <math>C=0</math>, dann ist <math>F</math> die Flächeninhaltsfunktion zu <math>f</math>. | ||
<html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/r-iUbclLabI?si=a5pPkIEuYHEhuoWi" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" referrerpolicy="strict-origin-when-cross-origin" allowfullscreen></iframe></html> | <html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/r-iUbclLabI?si=a5pPkIEuYHEhuoWi" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" referrerpolicy="strict-origin-when-cross-origin" allowfullscreen></iframe></html> | ||
| Zeile 10: | Zeile 10: | ||
==Bestimmtes Integral== | ==Bestimmtes Integral== | ||
Das '''bestimmte Integral''' einer [[Stetige_Funktion|stetigen Funktion]] <math>f</math> auf dem Intervall <math>[a; b]</math> ist durch | Das '''bestimmte Integral''' einer [[Stetige_Funktion|stetigen Funktion]] <math>f</math> auf dem Intervall <math>[a; b]</math> ist durch | ||
:<math>\int_a^b f(x) dx</math> | :<math>\int_a^b f(x) \, dx</math> | ||
gegeben. | gegeben. | ||
Für auf den Intervallen <math>[a;b] \subseteq [a;c]</math> und <math>[b;c] \subseteq [a;c]</math> stetige Funktionen <math>f, ~g</math> gelten die folgenden Rechenregeln: | |||
===Faktorregel=== | |||
:<math>\int_a^b c \cdot f(x) \, dx=c \cdot \int_a^b f(x) \, dx</math> | |||
===Summenregel=== | |||
:<math>\int_a^b (f(x)+g(x)) \, dx = \int_a^b f(x) \, dx + \int_a^bg(x) \, dx</math> | |||
===Intervalladditivität=== | |||
:<math>\int_a^c f(x) \, dx=\int_a^b f(x) \, dx+\int_b^c f(x) \, dx</math> | |||
===Vertauschen der Integrationsgrenzen=== | |||
:<math>\int_a^b f(x) \, dx=-\int_b^a f(x) \, dx</math> | |||
==Definition== | ==Definition== | ||
Falls <math>F</math> eine [[Stammfunktion]] von <math>f</math> ist, so wird das bestimmte Integral von auf dem Intervall <math>[a;b]</math> durch die Gleichung | Falls <math>F</math> eine [[Stammfunktion]] von <math>f</math> ist, so wird das bestimmte Integral von <math>f</math> auf dem Intervall <math>[a;b]</math> durch die Gleichung | ||
:<math>\int_a^b f(x) \, dx = F(b) - F(a)</math> | :<math>\int_a^b f(x) \, dx = F(b) - F(a)</math> | ||
berechnet. | berechnet. | ||
Hierbei bezeichnet <math>a</math> die untere und <math>b</math> die obere Grenze des Integrals. Das bestimmte Integral gibt den orientierten Flächeninhalt an, das heißt: | Hierbei bezeichnet <math>a</math> die untere und <math>b</math> die obere Grenze des Integrals. Das bestimmte Integral gibt den '''orientierten Flächeninhalt''' an, das heißt: | ||
* Liegt der Graph von <math>f</math> oberhalb der x-Achse, ist das | * Liegt der Graph von <math>f</math> oberhalb der x-Achse, ist das bestimmte Integral positiv. | ||
* Liegt der Graph von <math>f</math> unterhalb der x-Achse, ist das bestimmte Integral negativ. | * Liegt der Graph von <math>f</math> unterhalb der x-Achse, ist das bestimmte Integral negativ. | ||
* Liegt der Graph von <math>f</math> sowohl unterhalb als auch oberhalb der x-Achse, ist das bestimmte Integral die Differenz aus dem oberen Flächeninhalt und dem unteren Flächeninhalt. | * Liegt der Graph von <math>f</math> sowohl unterhalb als auch oberhalb der x-Achse, ist das bestimmte Integral die Differenz aus dem oberen Flächeninhalt und dem unteren Flächeninhalt. | ||
<html> | |||
<head> | |||
<script type="text/javascript" src="https://cdnjs.cloudflare.com/ajax/libs/jsxgraph/1.4.6/jsxgraphcore.js"></script> | |||
</head> | |||
<body> | |||
<div id="box2" style="width: 90vw; max-width: 400px; height: 60vw; max-height: 300px; margin-top:20px;"></div> | |||
<script type="text/javascript"> | |||
JXG.Options.text.useMathJax = true; | |||
// JSXGraph-Board erstellen | |||
var board = JXG.JSXGraph.initBoard('box2', { | |||
boundingbox: [-5, 5, 10, -5], // Angepasste Boundingbox für die Skalierung | |||
axis: true, | |||
showCopyright: false, | |||
showNavigation: true, | |||
grid: true, // Gitternetz aktivieren | |||
defaultAxes: { | |||
x: { | |||
withLabel: true, | |||
name: '\\[t\\]', | |||
label: { | |||
position: 'rt', | |||
offset: [-5, 20], | |||
fontSize: 14, | |||
anchorX: 'right' | |||
}, | |||
ticks: { | |||
ticksDistance: 1, | |||
minorTicks: 0 | |||
} | |||
}, | |||
y: { | |||
withLabel: true, | |||
name: '\\[f(t)\\]', | |||
label: { | |||
position: 'rt', | |||
offset: [5, 20], | |||
fontSize: 14, | |||
anchorY: 'right' | |||
}, | |||
ticks: { | |||
ticksDistance: 1, | |||
minorTicks: 0 | |||
} | |||
} | |||
} | |||
}); | |||
// Funktion erstellen | |||
var c1 = board.create('functiongraph', [function(t) { | |||
return (Math.pow(t, 5) / 24 - Math.pow(t, 3) / 2 + t); | |||
}]); | |||
// Integral erstellen | |||
var i1 = board.create('integral', [ | |||
[-2.0, 2.0], c1 | |||
], { | |||
withLabel: true, | |||
label: { | |||
fontSize: 14, | |||
offset: [0, 50], | |||
digits: 4, | |||
intl: { | |||
enabled: false, | |||
options: {} | |||
} | |||
}, | |||
baseLeft: { // Start point | |||
visible: true, | |||
fixed: false, | |||
withLabel: true, | |||
name: 'a' | |||
}, | |||
baseRight: { // End point | |||
visible: true, | |||
fixed: false, | |||
withLabel: true, | |||
name: 'b' | |||
} | |||
}); | |||
// Integral-Label anpassen | |||
i1.label.setText(() => { | |||
const a = i1.baseLeft.X().toFixed(2); // Untere Grenze | |||
const b = i1.baseRight.X().toFixed(2); // Obere Grenze | |||
const value = i1.Value().toFixed(4); // Wert des Integrals | |||
return `\\[\\int_{${a}}^{${b}} f(t) \\, dt = ${value}\\]`; | |||
}); | |||
// Beschriftung der Funktion mit f | |||
board.create('text', [3.5, 3, '\\[f\\]'], { | |||
fontSize: 14, | |||
fixed: true, | |||
anchorX: 'left', | |||
anchorY: 'bottom', | |||
color: 'blue' | |||
}); | |||
</script> | |||
</body> | |||
</html> | |||
<html><iframe width="280" height="157,5" src="https://www.youtube.com/embed/MX_WQS5-vAg?si=N2TxoCi_PHsr1_1B" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" referrerpolicy="strict-origin-when-cross-origin" allowfullscreen></iframe></html> | |||
==Integralfunktion== | ==Integralfunktion== | ||
Es sei <math>f</math> eine auf dem Intervall <math>[a;b]</math> [[stetige Funktion]], dann ist | Es sei <math>f</math> eine auf dem Intervall <math>[a;b]</math> [[stetige Funktion]], dann ist | ||
:<math>I_a(x)=\int_a^x f(t) | :<math>I_a(x)=\int_a^x f(t) \, dt</math> | ||
die dazugehörige '''Integralfunktion'''. | die dazugehörige '''Integralfunktion'''. | ||
==Flächen zwischen Funktionsgraphen ermitteln== | |||
Es seien <math>f, ~g</math> auf dem Intervall <math>[a;b]</math> stetige Funktionen. Die Fläche zwischen den Graphen von <math>f, ~g</math> wird wie folgt ermittelt: | |||
# Schnittstellen <math>x_{S_1},\dots,x_{S_n}</math> mit <math>n \in \mathbb{N}</math> der Graphen von <math>f, ~g</math> ermitteln. | |||
# Stammfunktionen <math>F,~G</math> ermitteln | |||
# <math>A=|\int_{x_{S_1}}^{x_{S_2}}(f(x)-g(x)) \, dx|+|\int_{x_{S_2}}^{x_{S_3}}(f(x)-g(x)) \, dx|+\dots+|\int_{x_{S_{n-1}}}^{x_{S_n}}(f(x)-g(x)) \, dx|</math> berechnen. (siehe [[Betragsfunktion]]) | |||
==Beispiele== | ==Beispiele== | ||
===Flächeninhalt ermitteln=== | ===Flächeninhalt ermitteln=== | ||
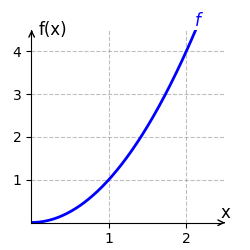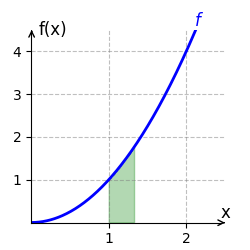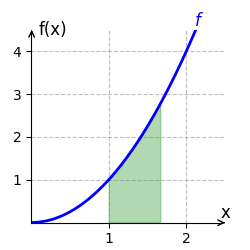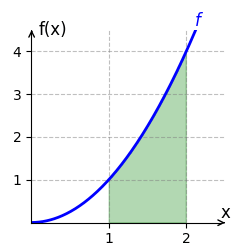
[[Datei:HauptsatzIntBspx2.gif|mini|Das bestimmte Integral der Funktion <span style="color:blue"><math>f(x)=x^2</math></span> auf dem Intervall <math>[1;2] </math> berechnet sich durch <span style="color:green"><math>\int_1^2 x^2 \, dx=\frac{7}{3}</math></span>.]] | |||
Wir berechnen das bestimmte Integral von <math>f(x) = x^2</math> auf dem Intervall <math>[1;2]</math>. | Wir berechnen das bestimmte Integral von <math>f(x) = x^2</math> auf dem Intervall <math>[1;2]</math>. | ||
Eine Stammfunktion von <math>f</math> ist <math>F(x) = \frac{x^3}{3}</math>. | Eine Stammfunktion von <math>f</math> ist <math>F(x) = \frac{x^3}{3}</math>. | ||
Das bestimmte Integral auf dem Intervall [1;2] wird durch | Das bestimmte Integral auf dem Intervall [1;2] wird durch | ||
:<math>\int_1^2 x^2 | :<math>\int_1^2 x^2 \, dx = F(2) - F(1)</math> | ||
:<math>= \frac{2^3}{3} - \frac{1^3}{3} = \frac{8}{3} - \frac{1}{3} = \frac{7}{3}</math> | :<math>= \frac{2^3}{3} - \frac{1^3}{3} = \frac{8}{3} - \frac{1}{3} = \frac{7}{3}</math> | ||
berechnet. | berechnet. | ||
Der Graph von <math>f</math> verläuft auf dem Intervall <math>[1;2]</math> oberhalb der x-Achse. Der | Der Graph von <math>f</math> verläuft auf dem Intervall <math>[1;2]</math> oberhalb der x-Achse. Der Flächeninhalt beträgt somit <math>\frac{7}{3}</math> Einheiten und ist im rechten Bild grün eingezeichnet. | ||
[[ | Wir berechnen den Flächeninhalt zwischen dem Graphen von \(f(t)=\frac{t^5}{24}-\frac{t^3}{2}+t\) und der x-Achse auf dem Intervall <math>[-2;2]</math> (siehe [[Hauptsatz_der_Differential-_und_Integralrechnung#Definition|Graph von <math>f</math>]]). | ||
1. Nullstellen von <math>f</math> berechnen | |||
:<math>\frac{t^5}{24}-\frac{t^3}{2}+t=0</math> | |||
:<math>t \approx -3,08 \lor t \approx -1,59 \lor t \approx 0 \lor t \approx 1,59 \lor t \approx 3,08</math> | |||
:<math>-1,59; 0; 1,59 \in [-2;2]</math> | |||
2. Flächeninhalt ermitteln | |||
:<math>A=|\int_{-2}^{-1,59} f(t) \, dt|+|\int_{-1,59}^{0} f(t) \, dt|+|\int_{0}^{1,59} f(t) \, dt|+|\int_{1,59}^{2} f(t) \, dt| </math> | |||
:<math>\approx |0,13|+|-0,58|+|0,58|+|-0,13| = 0,13+0,58+0,58+0,13= 1,42</math> | |||
Der gesuchte Flächeninhalt beträgt <math>A=1,42</math>. Der orientierte Flächeninhalt auf dem Intervall <math>[-2;2]</math> beträgt <math>\int_{-2}^{2} f(t) \, dt=0</math>. | |||
===Orientierten Flächeninhalt ermitteln=== | ===Orientierten Flächeninhalt ermitteln=== | ||
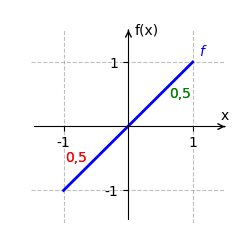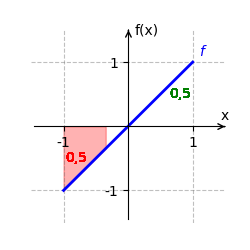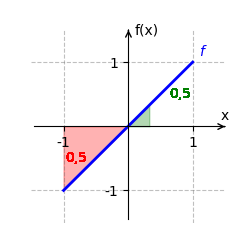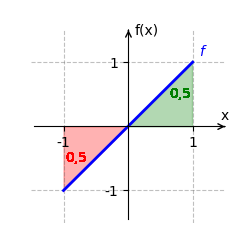
[[Datei:HauptsatzIntBspx.gif|mini|Das bestimmte Integral der Funktion <span style="color:blue"><math>f(x)=x</math></span> auf dem Intervall <math>[-1;1] </math> berechnet sich durch <math>\int_{-1}^1 x \, dx=</math><span style="color:green"><math>\frac{1}{2}</math></span><span style="color:red"><math>-</math><math>\frac{1}{2}</math></span><math>=0</math>.]] | |||
Wir betrachten <math>f(x) = x</math> auf dem Intervall <math>[-1;1]</math>. | Wir betrachten <math>f(x) = x</math> auf dem Intervall <math>[-1;1]</math>. | ||
Eine Stammfunktion von <math>f</math> ist <math>F(x) = \frac{x^2}{2}</math>. | Eine Stammfunktion von <math>f</math> ist <math>F(x) = \frac{x^2}{2}</math>. | ||
| Zeile 48: | Zeile 181: | ||
:<math>= \frac{1^2}{2} - \frac{(-1)^2}{2} = \frac{1}{2} - \frac{1}{2} = 0</math>. | :<math>= \frac{1^2}{2} - \frac{(-1)^2}{2} = \frac{1}{2} - \frac{1}{2} = 0</math>. | ||
Der orientierte Flächeninhalt beträgt <math>0</math>, da sich die positiven und negativen Flächeninhalte genau ausgleichen. | Der orientierte Flächeninhalt beträgt <math>0</math>, da sich die positiven und negativen Flächeninhalte genau ausgleichen. | ||
===Integralfunktion ermitteln=== | ===Integralfunktion ermitteln=== | ||
| Zeile 55: | Zeile 186: | ||
Die Integralfunktion ist: | Die Integralfunktion ist: | ||
:<math>I_0(x) = \int_0^x 3t \, dt</math>. | :<math>I_0(x) = \int_0^x 3t \, dt</math>. | ||
Eine Stammfunktion von <math>3t</math> ist <math>\frac{3t^2}{2}</math>, also | Eine Stammfunktion von <math>3t</math> ist <math>\frac{3t^2}{2}</math>, also gilt | ||
:<math>I_0(x) = \frac{3x^2}{2} - \frac{3 \cdot 0^2}{2} = \frac{3x^2}{2}</math>. | :<math>I_0(x) = \frac{3x^2}{2} - \frac{3 \cdot 0^2}{2} = \frac{3x^2}{2}</math>. | ||
===Flächeninhalt zwischen den Graphen von zwei Funktionen ermitteln=== | |||
[[Datei:HauptsatzIntFlächenZwGraphen.gif|mini|Fläche zwischen den Graphen von zwei Funktionen ermitteln]] | |||
Wir betrachten die Funktionen <math>f(x)=x^2+1</math> und <math>g(x)=-x^2+3</math> und ermitteln die Fläche zwischen den Graphen der Funktionen. | |||
1. Schnittstellen von <math>g,~f</math> ermitteln <br> | |||
:<math>f(x)=g(x)</math> | |||
:<math>x^2+1=-x^2+3</math> | |||
:<math>2 \cdot x^2=2</math> | |||
:<math> x^2=1</math> | |||
:<math> x=\pm \sqrt{1}</math> | |||
:<math>x=\pm 1</math> | |||
2. Stammfunktionen ermitteln | |||
:<math>F(x)=\frac{1}{3}x^3+x</math> | |||
:<math>G(x)=-\frac{1}{3}x^3+3x</math> | |||
3. Flächeninhalt ermitteln | |||
:<math>\int_{-1}^{1}(f(x)-g(x)) \, dx=F(1)-G(1)-(F(-1)-G(-1))</math> | |||
:<math>=\frac{1}{3} \cdot 1^3+1-(-\frac{1}{3}\cdot 1^3+3 \cdot 1)</math> | |||
:<math>-(\frac{1}{3} \cdot (-1)^3+(-1)-(-\frac{1}{3}\cdot (-1)^3+3 \cdot (-1)))</math> | |||
:<math>=-\frac{8}{3}</math> (orientierter Flächeninhalt) | |||
Der gesuchte Flächeninhalt ist der [[Betragsfunktion|Betrag]] der Zahl und beträgt <span style="color:green"><math>\frac{8}{3}</math></span>. | |||
[[Kategorie:Integralrechnung]] | [[Kategorie:Integralrechnung]] | ||
[[Kategorie:AHR_WuV_Mathe_GK]] | [[Kategorie:AHR_WuV_Mathe_GK]] | ||
Aktuelle Version vom 24. Februar 2025, 08:40 Uhr
Mit Hilfe des Hauptsatzes der Differential- und Integralrechnung werden Flächeninhalte zwischen dem Graphen einer Funktion der x-Achse berechnet.
Flächeninhaltsfunktion und Stammfunktion
Der Flächeninhalt zwischen dem Graphen einer Funktion [math]\displaystyle{ f }[/math] und der x-Achse im Intervall [math]\displaystyle{ [0;x] }[/math] wird durch den Funktionswert einer Flächeninhaltsfunktion [math]\displaystyle{ A }[/math] ermittelt.
Es sei [math]\displaystyle{ F }[/math] die Stammfunktion zu einer ganzrationalen Funktion [math]\displaystyle{ f }[/math] mit der Konstanten [math]\displaystyle{ C=0 }[/math], dann ist [math]\displaystyle{ F }[/math] die Flächeninhaltsfunktion zu [math]\displaystyle{ f }[/math].
Bestimmtes Integral
Das bestimmte Integral einer stetigen Funktion [math]\displaystyle{ f }[/math] auf dem Intervall [math]\displaystyle{ [a; b] }[/math] ist durch
- [math]\displaystyle{ \int_a^b f(x) \, dx }[/math]
gegeben.
Für auf den Intervallen [math]\displaystyle{ [a;b] \subseteq [a;c] }[/math] und [math]\displaystyle{ [b;c] \subseteq [a;c] }[/math] stetige Funktionen [math]\displaystyle{ f, ~g }[/math] gelten die folgenden Rechenregeln:
Faktorregel
- [math]\displaystyle{ \int_a^b c \cdot f(x) \, dx=c \cdot \int_a^b f(x) \, dx }[/math]
Summenregel
- [math]\displaystyle{ \int_a^b (f(x)+g(x)) \, dx = \int_a^b f(x) \, dx + \int_a^bg(x) \, dx }[/math]
Intervalladditivität
- [math]\displaystyle{ \int_a^c f(x) \, dx=\int_a^b f(x) \, dx+\int_b^c f(x) \, dx }[/math]
Vertauschen der Integrationsgrenzen
- [math]\displaystyle{ \int_a^b f(x) \, dx=-\int_b^a f(x) \, dx }[/math]
Definition
Falls [math]\displaystyle{ F }[/math] eine Stammfunktion von [math]\displaystyle{ f }[/math] ist, so wird das bestimmte Integral von [math]\displaystyle{ f }[/math] auf dem Intervall [math]\displaystyle{ [a;b] }[/math] durch die Gleichung
- [math]\displaystyle{ \int_a^b f(x) \, dx = F(b) - F(a) }[/math]
berechnet.
Hierbei bezeichnet [math]\displaystyle{ a }[/math] die untere und [math]\displaystyle{ b }[/math] die obere Grenze des Integrals. Das bestimmte Integral gibt den orientierten Flächeninhalt an, das heißt:
- Liegt der Graph von [math]\displaystyle{ f }[/math] oberhalb der x-Achse, ist das bestimmte Integral positiv.
- Liegt der Graph von [math]\displaystyle{ f }[/math] unterhalb der x-Achse, ist das bestimmte Integral negativ.
- Liegt der Graph von [math]\displaystyle{ f }[/math] sowohl unterhalb als auch oberhalb der x-Achse, ist das bestimmte Integral die Differenz aus dem oberen Flächeninhalt und dem unteren Flächeninhalt.
Integralfunktion
Es sei [math]\displaystyle{ f }[/math] eine auf dem Intervall [math]\displaystyle{ [a;b] }[/math] stetige Funktion, dann ist
- [math]\displaystyle{ I_a(x)=\int_a^x f(t) \, dt }[/math]
die dazugehörige Integralfunktion.
Flächen zwischen Funktionsgraphen ermitteln
Es seien [math]\displaystyle{ f, ~g }[/math] auf dem Intervall [math]\displaystyle{ [a;b] }[/math] stetige Funktionen. Die Fläche zwischen den Graphen von [math]\displaystyle{ f, ~g }[/math] wird wie folgt ermittelt:
- Schnittstellen [math]\displaystyle{ x_{S_1},\dots,x_{S_n} }[/math] mit [math]\displaystyle{ n \in \mathbb{N} }[/math] der Graphen von [math]\displaystyle{ f, ~g }[/math] ermitteln.
- Stammfunktionen [math]\displaystyle{ F,~G }[/math] ermitteln
- [math]\displaystyle{ A=|\int_{x_{S_1}}^{x_{S_2}}(f(x)-g(x)) \, dx|+|\int_{x_{S_2}}^{x_{S_3}}(f(x)-g(x)) \, dx|+\dots+|\int_{x_{S_{n-1}}}^{x_{S_n}}(f(x)-g(x)) \, dx| }[/math] berechnen. (siehe Betragsfunktion)
Beispiele
Flächeninhalt ermitteln
Wir berechnen das bestimmte Integral von [math]\displaystyle{ f(x) = x^2 }[/math] auf dem Intervall [math]\displaystyle{ [1;2] }[/math]. Eine Stammfunktion von [math]\displaystyle{ f }[/math] ist [math]\displaystyle{ F(x) = \frac{x^3}{3} }[/math]. Das bestimmte Integral auf dem Intervall [1;2] wird durch
- [math]\displaystyle{ \int_1^2 x^2 \, dx = F(2) - F(1) }[/math]
- [math]\displaystyle{ = \frac{2^3}{3} - \frac{1^3}{3} = \frac{8}{3} - \frac{1}{3} = \frac{7}{3} }[/math]
berechnet. Der Graph von [math]\displaystyle{ f }[/math] verläuft auf dem Intervall [math]\displaystyle{ [1;2] }[/math] oberhalb der x-Achse. Der Flächeninhalt beträgt somit [math]\displaystyle{ \frac{7}{3} }[/math] Einheiten und ist im rechten Bild grün eingezeichnet.
Wir berechnen den Flächeninhalt zwischen dem Graphen von \(f(t)=\frac{t^5}{24}-\frac{t^3}{2}+t\) und der x-Achse auf dem Intervall [math]\displaystyle{ [-2;2] }[/math] (siehe Graph von [math]\displaystyle{ f }[/math]).
1. Nullstellen von [math]\displaystyle{ f }[/math] berechnen
- [math]\displaystyle{ \frac{t^5}{24}-\frac{t^3}{2}+t=0 }[/math]
- [math]\displaystyle{ t \approx -3,08 \lor t \approx -1,59 \lor t \approx 0 \lor t \approx 1,59 \lor t \approx 3,08 }[/math]
- [math]\displaystyle{ -1,59; 0; 1,59 \in [-2;2] }[/math]
2. Flächeninhalt ermitteln
- [math]\displaystyle{ A=|\int_{-2}^{-1,59} f(t) \, dt|+|\int_{-1,59}^{0} f(t) \, dt|+|\int_{0}^{1,59} f(t) \, dt|+|\int_{1,59}^{2} f(t) \, dt| }[/math]
- [math]\displaystyle{ \approx |0,13|+|-0,58|+|0,58|+|-0,13| = 0,13+0,58+0,58+0,13= 1,42 }[/math]
Der gesuchte Flächeninhalt beträgt [math]\displaystyle{ A=1,42 }[/math]. Der orientierte Flächeninhalt auf dem Intervall [math]\displaystyle{ [-2;2] }[/math] beträgt [math]\displaystyle{ \int_{-2}^{2} f(t) \, dt=0 }[/math].
Orientierten Flächeninhalt ermitteln
Wir betrachten [math]\displaystyle{ f(x) = x }[/math] auf dem Intervall [math]\displaystyle{ [-1;1] }[/math]. Eine Stammfunktion von [math]\displaystyle{ f }[/math] ist [math]\displaystyle{ F(x) = \frac{x^2}{2} }[/math]. Das bestimmte Integral ist:
- [math]\displaystyle{ \int_{-1}^1 x \, dx = F(1) - F(-1) }[/math]
- [math]\displaystyle{ = \frac{1^2}{2} - \frac{(-1)^2}{2} = \frac{1}{2} - \frac{1}{2} = 0 }[/math].
Der orientierte Flächeninhalt beträgt [math]\displaystyle{ 0 }[/math], da sich die positiven und negativen Flächeninhalte genau ausgleichen.
Integralfunktion ermitteln
Gegeben sei [math]\displaystyle{ f(x) = 3x }[/math] und [math]\displaystyle{ a = 0 }[/math]. Die Integralfunktion ist:
- [math]\displaystyle{ I_0(x) = \int_0^x 3t \, dt }[/math].
Eine Stammfunktion von [math]\displaystyle{ 3t }[/math] ist [math]\displaystyle{ \frac{3t^2}{2} }[/math], also gilt
- [math]\displaystyle{ I_0(x) = \frac{3x^2}{2} - \frac{3 \cdot 0^2}{2} = \frac{3x^2}{2} }[/math].
Flächeninhalt zwischen den Graphen von zwei Funktionen ermitteln
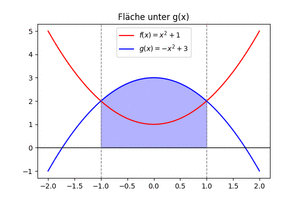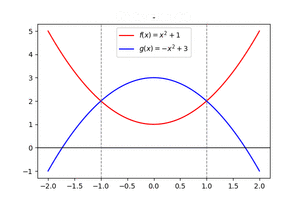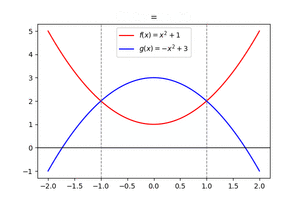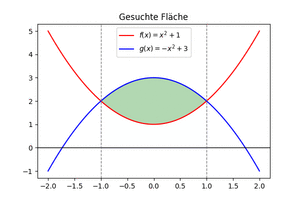
Wir betrachten die Funktionen [math]\displaystyle{ f(x)=x^2+1 }[/math] und [math]\displaystyle{ g(x)=-x^2+3 }[/math] und ermitteln die Fläche zwischen den Graphen der Funktionen.
1. Schnittstellen von [math]\displaystyle{ g,~f }[/math] ermitteln
- [math]\displaystyle{ f(x)=g(x) }[/math]
- [math]\displaystyle{ x^2+1=-x^2+3 }[/math]
- [math]\displaystyle{ 2 \cdot x^2=2 }[/math]
- [math]\displaystyle{ x^2=1 }[/math]
- [math]\displaystyle{ x=\pm \sqrt{1} }[/math]
- [math]\displaystyle{ x=\pm 1 }[/math]
2. Stammfunktionen ermitteln
- [math]\displaystyle{ F(x)=\frac{1}{3}x^3+x }[/math]
- [math]\displaystyle{ G(x)=-\frac{1}{3}x^3+3x }[/math]
3. Flächeninhalt ermitteln
- [math]\displaystyle{ \int_{-1}^{1}(f(x)-g(x)) \, dx=F(1)-G(1)-(F(-1)-G(-1)) }[/math]
- [math]\displaystyle{ =\frac{1}{3} \cdot 1^3+1-(-\frac{1}{3}\cdot 1^3+3 \cdot 1) }[/math]
- [math]\displaystyle{ -(\frac{1}{3} \cdot (-1)^3+(-1)-(-\frac{1}{3}\cdot (-1)^3+3 \cdot (-1))) }[/math]
- [math]\displaystyle{ =-\frac{8}{3} }[/math] (orientierter Flächeninhalt)
Der gesuchte Flächeninhalt ist der Betrag der Zahl und beträgt [math]\displaystyle{ \frac{8}{3} }[/math].