Histogramm
Die Wahrscheinlichkeitsverteilung eines Zufallsexperiments wird durch ein Histogramm visualisiert.
Definition
Es sei die Wahrscheinlichkeitsverteilung zu einem Zufallsexperiment gegeben. Ein Säulendiagramm, bei dem der Flächeninhalt einer Säule die Wahrscheinlichkeit des dazugehörigen Ergebnisses ist, heißt Histogramm. Die Höhe einer Säule wird als Wahrscheinlichkeitsdichte [math]\displaystyle{ \rho }[/math] (roh) bezeichnet. Die Breite einer Säule gibt an, wie viele Ergebnisse durch die Säule repräsentiert werden. Somit ergibt die Wahrscheinlichkeitsdichte [math]\displaystyle{ \rho_K }[/math] multipliziert mit der Breite [math]\displaystyle{ b_K }[/math] die Wahrscheinlichkeit des Ereignisses [math]\displaystyle{ K }[/math]; [math]\displaystyle{ P(K)=\rho_K\cdot b_K }[/math].
Beispiel
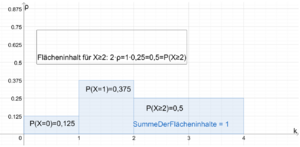
Histogramm zum dreifachen Münzwurf
Die folgenden beiden Histogramme visualisieren die Wahrscheinlichkeiten zum Zufallsexperiment des dreifachen Münzwurfs.
Histogramm der Binomialverteilung
html> <head>
<script type="text/javascript" src="https://cdnjs.cloudflare.com/ajax/libs/jsxgraph/1.4.6/jsxgraphcore.js"></script>
</head> <body>
<script type="text/javascript">
JXG.Options.text.useMathJax = true;
// JSXGraph-Board erstellen
var board = JXG.JSXGraph.initBoard('box2', {
boundingbox: [-5, 5, 10, -5], // Angepasste Boundingbox für die Skalierung
axis: true,
showCopyright: false,
showNavigation: true,
grid: true, // Gitternetz aktivieren
defaultAxes: {
x: {
withLabel: true,
name: '\\[t\\]',
label: {
position: 'rt',
offset: [-5, 20],
fontSize: 14,
anchorX: 'right'
},
ticks: {
ticksDistance: 1,
minorTicks: 0
}
},
y: {
withLabel: true,
name: '\\[f(t)\\]',
label: {
position: 'rt',
offset: [5, 20],
fontSize: 14,
anchorY: 'right'
},
ticks: {
ticksDistance: 1,
minorTicks: 0
}
}
}
});
// Funktion erstellen
var c1 = board.create('functiongraph', [function(t) {
return (Math.pow(t, 5) / 24 - Math.pow(t, 3) / 2 + t);
}]);
// Integral erstellen
var i1 = board.create('integral', [
[-2.0, 2.0], c1
], {
withLabel: true,
label: {
fontSize: 14,
offset: [0, 50],
digits: 4,
intl: {
enabled: false,
options: {}
}
},
baseLeft: { // Start point
visible: true,
fixed: false,
withLabel: true,
name: 'a'
},
baseRight: { // End point
visible: true,
fixed: false,
withLabel: true,
name: 'b'
}
});
// Integral-Label anpassen
i1.label.setText(() => {
const a = i1.baseLeft.X().toFixed(2); // Untere Grenze
const b = i1.baseRight.X().toFixed(2); // Obere Grenze
const value = i1.Value().toFixed(4); // Wert des Integrals
return `\\[\\int_{${a}}^{${b}} f(t) \\, dt = ${value}\\]`;
});
// Beschriftung der Funktion mit f
board.create('text', [3.5, 3, '\\[f\\]'], {
fontSize: 14,
fixed: true,
anchorX: 'left',
anchorY: 'bottom',
color: 'blue'
});
</script>
</body> </html>