Baumdiagramm: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| Zeile 2: | Zeile 2: | ||
Ein '''Baumdiagramm''' stellt die möglichen [[Zufallsexperiment#Definition|Ergebnisse]] eines [[Zufallsexperiment|Zufallsexperiments]] grafisch dar. Es dient dazu, die [[Wahrscheinlichkeitsverteilung]] der möglichen Ergebnisse zu berechnen und zu visualisieren. | Ein '''Baumdiagramm''' stellt die möglichen [[Zufallsexperiment#Definition|Ergebnisse]] eines [[Zufallsexperiment|Zufallsexperiments]] grafisch dar. Es dient dazu, die [[Wahrscheinlichkeitsverteilung]] der möglichen Ergebnisse zu berechnen und zu visualisieren. | ||
Jeder '''Knoten''' eines Baumdiagramms repräsentiert ein bestimmtes Zwischenergebnis im Ablauf des Zufallsexperiments. Die Knoten sind durch '''Zweige''' verbunden. Jeder Zweig ist mit der Wahrscheinlichkeit beschriftet, mit der das Zwischenergebnis des verbundenen Knotens eintrifft. Ein '''Pfad''' ist eine Folge von Knoten, die durch Zweige miteinander verbunden sind. Ein Pfad der bei dem Anfangsknoten startet und bei einem Endknoten endet repräsentiert ein Ergebnis des Zufallsexperiments. Die Wahrscheinlichkeit des Ergebnisses wird an das Ende des Pfades geschrieben. | Jeder '''Knoten''' eines Baumdiagramms repräsentiert ein bestimmtes Zwischenergebnis im Ablauf des Zufallsexperiments. Die Knoten sind durch '''Zweige''' bzw. '''Kanten''' verbunden. Jeder Zweig ist mit der Wahrscheinlichkeit beschriftet, mit der das Zwischenergebnis des verbundenen Knotens eintrifft. Ein '''Pfad''' ist eine Folge von Knoten, die durch Zweige miteinander verbunden sind. Ein Pfad der bei dem Anfangsknoten startet und bei einem Endknoten endet repräsentiert ein Ergebnis des Zufallsexperiments. Die Wahrscheinlichkeit des Ergebnisses wird an das Ende des Pfades geschrieben. | ||
==Pfadmultiplikation== | <html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/cVmoFlKKJVE?si=5UQKeQHvXJgjtzYT" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | ||
==Wahrscheinlichkeiten im Baumdiagramm ermitteln== | |||
Zur Ermittlung der Wahrscheinlichkeiten in einem Baumdiagramm existieren die folgenden beiden Regeln. | |||
<iframe width="280" height="157.5" src="https://www.youtube.com/embed/ZWALk4haajQ?si=NeCjRGKV_jbnxEUk" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | |||
===Pfadmultiplikation=== | |||
Die '''Pfadmultiplikationsregel''' besagt, dass im Baumdiagramm die Wahrscheinlichkeit eines Pfades gleich dem Produkt der Wahrscheinlichkeiten auf den Teilstrecken des Pfades ist. | Die '''Pfadmultiplikationsregel''' besagt, dass im Baumdiagramm die Wahrscheinlichkeit eines Pfades gleich dem Produkt der Wahrscheinlichkeiten auf den Teilstrecken des Pfades ist. | ||
==Pfadaddition== | ===Pfadaddition=== | ||
Die '''Pfadadditionsregel''' besagt, dass im Baumdiagramm die Wahrscheinlichkeit eines Ereignisses gleich der Summe der Wahrscheinlichkeiten der in diesem Ereignis enthaltenen Ergebnisse sind. | Die '''Pfadadditionsregel''' besagt, dass im Baumdiagramm die Wahrscheinlichkeit eines Ereignisses gleich der Summe der Wahrscheinlichkeiten der in diesem Ereignis enthaltenen Ergebnisse sind. | ||
| Zeile 16: | Zeile 23: | ||
Eine Münze wird dreimal geworfen und man beobachtet, in welcher Reihenfolge Zahl (Z) und Kopf (K) oben liegen. Die [[Zufallsexperiment#Definition|Ergebnismenge]] ist dann <math>S = \{ZZZ; ZZK; ZKZ; ZKK; KZZ; KZK; KKZ; KKK\}</math>. | Eine Münze wird dreimal geworfen und man beobachtet, in welcher Reihenfolge Zahl (Z) und Kopf (K) oben liegen. Die [[Zufallsexperiment#Definition|Ergebnismenge]] ist dann <math>S = \{ZZZ; ZZK; ZKZ; ZKK; KZZ; KZK; KKZ; KKK\}</math>. | ||
Die rechte Abbildung zeigt, wie eine Ergebnismenge <math>S</math> mit Hilfe eines Baumdiagramms dargestellt werden kann. Der erste Knoten ist der Anfangsknoten, von dem zwei Zweige zu den Knoten Z und K ausgehen. Diese beiden Knoten repräsentieren das Resultat des ersten Wurfs und damit ein Zwischenergebnis des [[Zufallsexperiment|Zufallsexperiments]]. Von diesen Knoten gehen Zweige zu den Knoten ab, die das Resultat des zweiten Wurfs repräsentieren. Das Prinzip wird fortgesetzt, bis ein Endknoten erreicht ist. Der Endknoten repräsentiert die letzte Stufe des Zufallsexperiments. Der Pfad Anfangsknoten; Z; K; Z repräsentiert beispielsweise das Ergebnis erster Wurf Zahl, zweiter Wurf Kopf und dritter Wurf Zahl ist. | |||
Das Ereignis, dass zwei- oder dreimal hintereinander Zahl erscheint, ist <math>B = \{ZZZ; ZZK; KZZ\}</math>. Ereignis <math>B</math> tritt also ein, wenn das Zufallsexperiment entlang einer zu Ereignis <math>B</math> gehörigen Kantenkombination führt (z. B. KZZ). | |||
Die Wahrscheinlichkeit für | ===Wahrscheinlichkeiten im Baumdiagramm ermitteln=== | ||
Die Wahrscheinlichkeit für jeden Zweig ist 0,5. Wir definieren eine [[Wahrscheinlichkeitsverteilung#Zufallsvariable|Zufallsvariable]] <math>X</math>, die die Häufigkeit von Zahl angibt. X kann dann die Werte 0, 1, 2 und 3 annehmen. Die Wahrscheinlichkeit für das Ereignis {ZZZ} ist: | |||
<math>P\left(ZZZ\right)=P(X=3)=0,5\cdot0,5\cdot0,5=0,125=12,5\%</math> (Pfadmultiplikation) | <math>P\left(ZZZ\right)=P(X=3)=0,5\cdot0,5\cdot0,5=0,125=12,5\%</math> (Pfadmultiplikation) | ||
| Zeile 29: | Zeile 35: | ||
<math>P\left(\{ZZZ;ZZK\} \right)=P(\{ZZZ\})+P(\{ZZK\})=0,125+0,125=0,25=25\%</math> (Pfadaddition) | <math>P\left(\{ZZZ;ZZK\} \right)=P(\{ZZZ\})+P(\{ZZK\})=0,125+0,125=0,25=25\%</math> (Pfadaddition) | ||
[[Kategorie:Wahrscheinlichkeitsrechnung]] | [[Kategorie:Wahrscheinlichkeitsrechnung]] | ||
[[Kategorie:Fachabitur]] | [[Kategorie:Fachabitur]] | ||
Version vom 18. Juli 2024, 09:42 Uhr
Definition
Ein Baumdiagramm stellt die möglichen Ergebnisse eines Zufallsexperiments grafisch dar. Es dient dazu, die Wahrscheinlichkeitsverteilung der möglichen Ergebnisse zu berechnen und zu visualisieren.
Jeder Knoten eines Baumdiagramms repräsentiert ein bestimmtes Zwischenergebnis im Ablauf des Zufallsexperiments. Die Knoten sind durch Zweige bzw. Kanten verbunden. Jeder Zweig ist mit der Wahrscheinlichkeit beschriftet, mit der das Zwischenergebnis des verbundenen Knotens eintrifft. Ein Pfad ist eine Folge von Knoten, die durch Zweige miteinander verbunden sind. Ein Pfad der bei dem Anfangsknoten startet und bei einem Endknoten endet repräsentiert ein Ergebnis des Zufallsexperiments. Die Wahrscheinlichkeit des Ergebnisses wird an das Ende des Pfades geschrieben.
Wahrscheinlichkeiten im Baumdiagramm ermitteln
Zur Ermittlung der Wahrscheinlichkeiten in einem Baumdiagramm existieren die folgenden beiden Regeln.
<iframe width="280" height="157.5" src="https://www.youtube.com/embed/ZWALk4haajQ?si=NeCjRGKV_jbnxEUk" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html>
Pfadmultiplikation
Die Pfadmultiplikationsregel besagt, dass im Baumdiagramm die Wahrscheinlichkeit eines Pfades gleich dem Produkt der Wahrscheinlichkeiten auf den Teilstrecken des Pfades ist.
Pfadaddition
Die Pfadadditionsregel besagt, dass im Baumdiagramm die Wahrscheinlichkeit eines Ereignisses gleich der Summe der Wahrscheinlichkeiten der in diesem Ereignis enthaltenen Ergebnisse sind.
Beispiele
Zufallsexperiment dreifacher Münzwurf grafisch darstellen
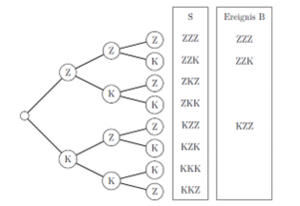
Eine Münze wird dreimal geworfen und man beobachtet, in welcher Reihenfolge Zahl (Z) und Kopf (K) oben liegen. Die Ergebnismenge ist dann [math]\displaystyle{ S = \{ZZZ; ZZK; ZKZ; ZKK; KZZ; KZK; KKZ; KKK\} }[/math].
Die rechte Abbildung zeigt, wie eine Ergebnismenge [math]\displaystyle{ S }[/math] mit Hilfe eines Baumdiagramms dargestellt werden kann. Der erste Knoten ist der Anfangsknoten, von dem zwei Zweige zu den Knoten Z und K ausgehen. Diese beiden Knoten repräsentieren das Resultat des ersten Wurfs und damit ein Zwischenergebnis des Zufallsexperiments. Von diesen Knoten gehen Zweige zu den Knoten ab, die das Resultat des zweiten Wurfs repräsentieren. Das Prinzip wird fortgesetzt, bis ein Endknoten erreicht ist. Der Endknoten repräsentiert die letzte Stufe des Zufallsexperiments. Der Pfad Anfangsknoten; Z; K; Z repräsentiert beispielsweise das Ergebnis erster Wurf Zahl, zweiter Wurf Kopf und dritter Wurf Zahl ist.
Das Ereignis, dass zwei- oder dreimal hintereinander Zahl erscheint, ist [math]\displaystyle{ B = \{ZZZ; ZZK; KZZ\} }[/math]. Ereignis [math]\displaystyle{ B }[/math] tritt also ein, wenn das Zufallsexperiment entlang einer zu Ereignis [math]\displaystyle{ B }[/math] gehörigen Kantenkombination führt (z. B. KZZ).
Wahrscheinlichkeiten im Baumdiagramm ermitteln
Die Wahrscheinlichkeit für jeden Zweig ist 0,5. Wir definieren eine Zufallsvariable [math]\displaystyle{ X }[/math], die die Häufigkeit von Zahl angibt. X kann dann die Werte 0, 1, 2 und 3 annehmen. Die Wahrscheinlichkeit für das Ereignis {ZZZ} ist:
[math]\displaystyle{ P\left(ZZZ\right)=P(X=3)=0,5\cdot0,5\cdot0,5=0,125=12,5\% }[/math] (Pfadmultiplikation)
Das Ereignis „die ersten beiden Würfe ergeben Zahl“ ist [math]\displaystyle{ \{ZZZ; ZZK\} }[/math] mit der Wahrscheinlichkeit:
[math]\displaystyle{ P\left(\{ZZZ;ZZK\} \right)=P(\{ZZZ\})+P(\{ZZK\})=0,125+0,125=0,25=25\% }[/math] (Pfadaddition)