Empirisches Gesetz der großen Zahlen: Unterschied zwischen den Versionen

Zum nächsten Versionsunterschied →

VisuellWikitext

@@ Zeile 1: / Zeile 1: @@
-Wird ein [[Zufallsexperiment]]
+Das empirische Gesetz der großen Zahlen ist eine Beobachtung, die besagt, dass [[Häufigkeit#Definition|relative Häufigkeiten]] von [[Zufallsexperiment#Ereignis|Ereignissen]] in großen [[H%C3%A4ufigkeit#Statistische_Begriffe|Stichproben]] den theoretischen [[Wahrscheinlichkeitsverteilung|Wahrscheinlichkeiten]] nahekommen.
 ==Definition==
-Wird ein Zufallsexperiment sehr oft durchgeführt, so ändern sich die relativen Häufigkeiten der einzelnen Ergebnisse nur noch wenig.
+Wird ein [[Zufallsexperiment]] sehr oft durchgeführt, so ändern sich die [[Häufigkeit#Definition|relativen Häufigkeiten]] der einzelnen [[Zufallsexperiment#Definition|Ergebnisse]] nur noch wenig. Je größer die Anzahl der Durchführungen eines Zufallsexperimentes ist, desto genauer nähert sich die relative Häufigkeit der [[Wahrscheinlichkeitsverteilung|Wahrscheinlichkeit]] eines [[Zufallsexperiment#Ereignis|Ereignisses]] an.
-Je größer die Anzahl der Durchführungen eines Zufallsexperimentes ist, desto genauer nähert sich die relative Häufigkeit der Wahrscheinlichkeit eines Ereignisses an.
 ==Beispiel==
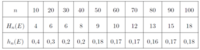
-Wir betrachten ein Würfelbeispiel. Ein Würfel wird 10-; 20-; ...; 100-mal geworfen. Es wird geprüft, wie oft das Ereignis <math>E = {2}</math> aufgetreten ist. Die Ergebnisse sind in der unteren Tabelle festgehalten. n gibt die Anzahl der Würfe an. <math>H_n\left(E\right)</math> gibt die absolute Häufigkeit von E und <math>h_n\left(E\right)</math> die relative Häufigkeit von E an.
+Wir betrachten ein Würfelbeispiel. Ein Würfel wird 10-; 20-; ...; 100-mal geworfen. Es wird geprüft, wie oft das [[Zufallsexperiment#Ereignis|Ereignis]] <math>E = {2}</math> aufgetreten ist. Die [[Zufallsexperiment#Ereignis|Ergebnisse]] sind in der unteren Tabelle festgehalten. n gibt die Anzahl der Würfe an. <math>H_n(E)</math> gibt die absolute Häufigkeit von <math>E</math> und <math>h_n\left(E\right)</math> die [[Häufigkeit|relative Häufigkeit]] von <math>E</math> an.
 <gallery widths=200 heights=100>Datei:WahrscheinlichkeitsrechnungGeZT.png|Ergebnisse Würfelspiel
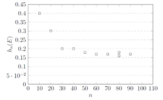
 Datei:WahrscheinlichkeitsrechnungGeZG.png|Punktdiagramm Würfelspiel
 </gallery>
-Am Anfang existieren starke Schwankungen der relativen Häufigkeiten des Ereignisses E, die aber mit wachsender Anzahl an Würfen abnehmen. Die relativen Häufigkeiten stabilisieren sich um den Wert 0,17. Diese Zahl wird als statistische Wahrscheinlichkeit für das Ereignis E bezeichnet. Beim idealen Würfel kann man aufgrund seiner Symmetrie die Annahme machen, dass die Augenzahlen 1,2,3,4,5 und 6 etwa gleich häufig auftreten, wenn man oft genug würfelt. Für das Ereignis E setzt man dann die Wahrscheinlichkeit P durch <math>P\left(E\right)=\frac{1}{6}\approx 0,17</math> fest.
+Am Anfang existieren starke Schwankungen der relativen Häufigkeiten des Ereignisses <math>E</math>, die aber mit wachsender Anzahl an Würfen abnehmen. Die relativen Häufigkeiten stabilisieren sich um den Wert 0,17. Diese Zahl wird als statistische [[Wahrscheinlichkeitsverteilung|Wahrscheinlichkeit]] für das Ereignis <math>E</math> bezeichnet. Beim idealen Würfel kann man aufgrund seiner Symmetrie die Annahme machen, dass die Augenzahlen 1,2,3,4,5 und 6 etwa gleich häufig auftreten, wenn man oft genug würfelt. Für das Ereignis <math>E</math> setzt man dann die Wahrscheinlichkeit <math>P</math> durch <math>P(E)=\frac{1}{6}\approx 0,17</math> fest.
 <html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/NcX5TpmC2zM?si=DTXAbz6NVVLsujje" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html>
 [[Kategorie:Wahrscheinlichkeitsrechnung]]