Histogramm: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „==Definition== Wahrscheinlichkeitsverteilungen werden durch '''Histogramme''' visualisiert. Der Flächeninhalt einer Säule gibt die Wahrscheinlichkeit der Ausprägung(en) der Zufallsvariablen an. Die Höhe einer Säule wird als Wahrscheinlichkeitsdichte <math>\rho</math> (roh) bezeichnet. Die Intervallbreite gibt an, wie viele Ausprägungen der Zufallsvariablen in die jeweilige Klasse fallen. Somit ergibt die Wahrscheinlichkeitsdichte multipliziert mit d…“ |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
Die [[Wahrscheinlichkeitsverteilung]] eines [[Zufallsexperiment|Zufallsexperiments]] wird durch ein Histogramm visualisiert. | |||
==Definition== | ==Definition== | ||
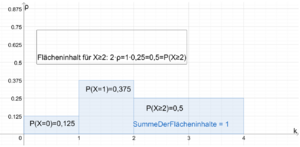
Es sei die [[Wahrscheinlichkeitsverteilung]] zu einem [[Zufallsexperiment]] gegeben. Ein [[Säulendiagramm]], bei dem der Flächeninhalt einer Säule die Wahrscheinlichkeit des dazugehörigen Ergebnisses ist, heißt '''Histogramm'''. Die Höhe einer Säule wird als '''Wahrscheinlichkeitsdichte''' <math>\rho</math> (roh) bezeichnet. Die Breite einer Säule gibt an, wie viele Ergebnisse durch die Säule repräsentiert werden. Somit ergibt die Wahrscheinlichkeitsdichte <math>\rho_K</math> multipliziert mit der Breite <math>b_K</math> die Wahrscheinlichkeit des Ereignisses <math>K</math>; <math>P(K)=\rho_K\cdot b_K</math>. | |||
<math>P | |||
<html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/rOWqpAA0pnE?si=GdtJ7rrgggzEhk56 | <html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/rOWqpAA0pnE?si=GdtJ7rrgggzEhk56" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | ||
==Beispiel== | ==Beispiel== | ||
===Histogramm zum dreifachen Münzwurf=== | |||
Die folgenden beiden Histogramme visualisieren die Wahrscheinlichkeiten zum Zufallsexperiment des dreifachen Münzwurfs. | Die folgenden beiden Histogramme visualisieren die Wahrscheinlichkeiten zum Zufallsexperiment des dreifachen Münzwurfs. | ||
| Zeile 13: | Zeile 14: | ||
Datei:WahrscheinlichkeitsrechnungHisto2.png | Datei:WahrscheinlichkeitsrechnungHisto2.png | ||
</gallery> | </gallery> | ||
===Histogramm der Binomialverteilung=== | |||
<html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/Lc_R0vBSKHw?si=V72WfOUjhQRQlrN9" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | |||
Version vom 18. Juli 2024, 09:37 Uhr
Die Wahrscheinlichkeitsverteilung eines Zufallsexperiments wird durch ein Histogramm visualisiert.
Definition
Es sei die Wahrscheinlichkeitsverteilung zu einem Zufallsexperiment gegeben. Ein Säulendiagramm, bei dem der Flächeninhalt einer Säule die Wahrscheinlichkeit des dazugehörigen Ergebnisses ist, heißt Histogramm. Die Höhe einer Säule wird als Wahrscheinlichkeitsdichte [math]\displaystyle{ \rho }[/math] (roh) bezeichnet. Die Breite einer Säule gibt an, wie viele Ergebnisse durch die Säule repräsentiert werden. Somit ergibt die Wahrscheinlichkeitsdichte [math]\displaystyle{ \rho_K }[/math] multipliziert mit der Breite [math]\displaystyle{ b_K }[/math] die Wahrscheinlichkeit des Ereignisses [math]\displaystyle{ K }[/math]; [math]\displaystyle{ P(K)=\rho_K\cdot b_K }[/math].
Beispiel
Histogramm zum dreifachen Münzwurf
Die folgenden beiden Histogramme visualisieren die Wahrscheinlichkeiten zum Zufallsexperiment des dreifachen Münzwurfs.
Histogramm der Binomialverteilung