Wendepunkt: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „==Definition== Es sei <math>f:\mathbb{D}_f \rightarrow \mathbb{W}_f</math> eine stetige Funktion. <math>W(x_0,f(x_0)</math> für <math>x_0 \in \mathbb{D}_f </math> heißt '''Wendepunkt''' von <math>f</math>, wenn an <math>W</math> ein Wechsel von einer Linkskurve in eine Rechtskurve oder umgekehrt von einer Monotone_Funktion#Kr%C3%BCmmung_einer_Funk…“ |
Keine Bearbeitungszusammenfassung |
||
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 17: | Zeile 17: | ||
'''Alternativ''' können wir <math>f'''</math> verwenden: | '''Alternativ''' können wir <math>f'''</math> verwenden: | ||
Ist <math>f | Ist <math>f''(x_0)=0</math> und <math>f'''(x_0)\neq0</math>, dann hat der Graph der Funktion <math>f</math> an der [[Funktion#Definition|Stelle]] <math>x_0</math> einen Wendepunkt. Gilt <math>f'''(x_0)>0</math>, hat der Graph bei <math>x_0</math> eine [[Monotone_Funktion#Kr%C3%BCmmung_einer_Funktion|Rechts-Linkskrümmung]]. Gilt <math>f'''(x_0)<0</math>, hat der Graph bei <math>x_0</math> eine eine [[Monotone_Funktion#Kr%C3%BCmmung_einer_Funktion|Links-Rechtskrümmung]]. | ||
===Funktionswert berechnen=== | ===Funktionswert berechnen=== | ||
Erfüllt ein <math>x_0 \in \mathbb{D}_f</math> die notwendige und die hinreichende Bedingung, dann ist <math>x_0</math> eine Wendestelle. Der Funktionswert wird dann durch <math>f(x_0)</math> berechnet. | Erfüllt ein <math>x_0 \in \mathbb{D}_f</math> die notwendige und die hinreichende Bedingung, dann ist <math>x_0</math> eine Wendestelle. Der Funktionswert wird dann durch <math>f(x_0)</math> berechnet. | ||
<html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/ZIYraiiPBE4?si=SLuTWYgSnrFxNtMf" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | <html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/ZIYraiiPBE4?si=SLuTWYgSnrFxNtMf" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | ||
==Beispiele== | ==Beispiele== | ||
====Kurvenübergänge graphisch erläutert==== | |||
[[Datei:WendepunktBeispielSin.gif|mini|[[Graph]] der Funktion <math>f(x)=sin(2x)</math>]] | |||
Im Bild auf der rechten Seite ist die [[Differenzenquotient#Tangente|Tangente]] während der Linkskurve <span style="color:blue">blau</span> und während der Rechtskurve <span style="color:green">grün</span> gefärbt. Die Wendepunkte befinden sich an den Punkten, in denen die Tangente die Farbe wechselt. | |||
====Wendepunkt für eine ganzrationale Funktion berechnen==== | |||
[[Datei:DifferentialrechnungWende.png|mini|Graph von <math>f\left(x\right)=x^4-3x^3-2x^2</math> mit Ableitungen]] | [[Datei:DifferentialrechnungWende.png|mini|Graph von <math>f\left(x\right)=x^4-3x^3-2x^2</math> mit Ableitungen]] | ||
Wir betrachten <math>f\left(x\right)=x^4-3x^3-2x^2</math> | Wir betrachten <span style="color:green"><math>f\left(x\right)=x^4-3x^3-2x^2</math></span> mit den Ableitungen <span style="color:blue"><math>f'\left(x\right)={4x}^3-9x^2-4x</math></span>, <span style="color:red"><math>f''\left(x\right)={12x}^2-18x-4</math></span> und <span style="color:orange"><math>f'''\left(x\right)=24x-18</math></span>. | ||
'''1. Notwendige Bedingung:''' | |||
<math>f''(x)=0</math> | |||
<math>12x^2-18x-4=0</math> | |||
<math>x_0\approx 1,696,~x_1\approx -0,196</math> | |||
'''2. Hinreichende Bedingung:''' | |||
<math>f'''(1,696) \approx 22,704</math> und <math>f'''(-0,196) \approx -22,704</math> | |||
Also geht an der [[Funktion#Definition|Stelle]] <math>x_0</math> der Graph von einer [[Monotone_Funktion#Kr%C3%BCmmung_einer_Funktion|Rechtskrümmung]] in eine [[Monotone_Funktion#Kr%C3%BCmmung_einer_Funktion|Linkskrümmung]] über. Bei <math>x_1</math> geht der Graph von einer [[Monotone_Funktion#Kr%C3%BCmmung_einer_Funktion|Linkskrümmung]] in eine [[Monotone_Funktion#Kr%C3%BCmmung_einer_Funktion|Rechtskrümmung]] über. | |||
'''3. Funktionswert berechnen:''' | |||
<math>f(1,696)\approx-12,121</math> und <math>f(x_1)\approx-0,052</math> | |||
<math>f</math> die Wendepunkte <math>W_0(1,696|-12,121)</math> und <math>W_1(-0,196|-0,052)</math>. | |||
====Sattelpunkt==== | |||
[[Datei:WendepunktSattelpunkt.png|mini|Graph der [[Funktion]] <math>f(x)=x^3</math>]] | |||
Wir betrachten die Funktion <math>f(x)=x^3</math> mit <math>f'(x)=3x^2,~f''(x)=6x,~f'''(x)=6~</math>. | |||
'''1. Notwendige Bedingung:''' | |||
<math>f''(x)=0</math> | |||
<math>6x=0</math> | |||
<math>x=0</math> | |||
'''2. Hinreichende Bedingung:''' | |||
<math>f'''(0)=6>0</math> | |||
Der [[Graph]] von <math>f</math> geht bei <math>x=0</math> von einer [[Monotone_Funktion#Kr%C3%BCmmung_einer_Funktion|Rechtskrümmung]] in eine [[Monotone_Funktion#Kr%C3%BCmmung_einer_Funktion|Linkskrümmung]] über. | |||
'''3. Funktionswert berechnen:''' | |||
<math>f | <math>f(0)=0</math> | ||
<math>f</math> | <math>f</math> den Wendepunkt <math>W(0|0)</math> | ||
Außerdem ist <math>W</math> ein Sattelpunkt, da <math>f'(0)=3 \cdot 0^2 =0</math> gilt. Die [[Extremwert#Notwendige_Bedingung_f%C3%BCr_Extremstellen|notwendige Bedingung]] für Extremwerte ist also ebenfalls erfüllt. Die Steigung in <math>W</math> ist <math>0</math>. | |||
[[Kategorie:Differentialrechnung]] | [[Kategorie:Differentialrechnung]] | ||
[[Kategorie: | [[Kategorie:FHR_WuV_Mathe]] | ||
[[Kategorie:AHR_WuV_Mathe_GK]] | |||
Aktuelle Version vom 11. November 2025, 09:13 Uhr
Definition
Es sei [math]\displaystyle{ f:\mathbb{D}_f \rightarrow \mathbb{W}_f }[/math] eine stetige Funktion. [math]\displaystyle{ W(x_0,f(x_0) }[/math] für [math]\displaystyle{ x_0 \in \mathbb{D}_f }[/math] heißt Wendepunkt von [math]\displaystyle{ f }[/math], wenn an [math]\displaystyle{ W }[/math] ein Wechsel von einer Linkskurve in eine Rechtskurve oder umgekehrt von einer Rechtskurve in eine Linkskurve stattfindet. Wir nennen das eine Links-Rechtskrümmung oder Rechts-Linkskrümmung. [math]\displaystyle{ x_0 }[/math] nennen wir dann Wendestelle.
Sattelpunkt
Es sei [math]\displaystyle{ f:\mathbb{D}_f \rightarrow \mathbb{W}_f }[/math] eine stetig differenzierbare Funktion und [math]\displaystyle{ x_0 }[/math] eine Wendestelle von [math]\displaystyle{ f }[/math]. Gilt [math]\displaystyle{ f'(x_0)=0 }[/math], heißt [math]\displaystyle{ (x_0|f(x_0)) }[/math] Sattelpunkt von [math]\displaystyle{ f }[/math].
Wendepunkt berechnen
Wendepunkte lassen sich mit Hilfe der Ableitungsfunktion bestimmen. Dafür werden die folgenden Bedingungen verwendet und anschließend wird der Funktionswert berechnet. Im Folgenden sei [math]\displaystyle{ f:\mathbb{D}_f \rightarrow \mathbb{W}_f }[/math] eine stetig differenzierbare Funktion mit [math]\displaystyle{ x_0 \in \mathbb{D}_f }[/math] und den Ableitungsfunktionen [math]\displaystyle{ f', f'' }[/math] und [math]\displaystyle{ f''' }[/math].
Notwendige Bedingung für Wendestellen
Hat [math]\displaystyle{ f }[/math] an der Stelle [math]\displaystyle{ x_0 }[/math] eine Wendestelle, so gilt [math]\displaystyle{ f''(x_0)=0 }[/math]. D. h. [math]\displaystyle{ x_0 }[/math] ist eine Nullstelle von [math]\displaystyle{ f'' }[/math].
Hinreichende Bedingung für Wendestellen
Hat [math]\displaystyle{ f'' }[/math] an der Stelle [math]\displaystyle{ x_0 }[/math] eine Nullstelle mit Vorzeichenwechsel, so hat der Graph von [math]\displaystyle{ f }[/math] an der Stelle [math]\displaystyle{ x_0 }[/math] einen Wendepunkt. Findet der Vorzeichenwechsel von negativ zu positiv statt, hat der Graph von [math]\displaystyle{ f }[/math] an der Stelle [math]\displaystyle{ x_0 }[/math] eine Rechts-Linkskrümmung. Findet der Vorzeichenwechsel von positiv zu negativ statt, hat der Graph von [math]\displaystyle{ f }[/math] an der Stelle [math]\displaystyle{ x_0 }[/math] eine Links-Rechtskrümmung.
Alternativ können wir [math]\displaystyle{ f''' }[/math] verwenden:
Ist [math]\displaystyle{ f''(x_0)=0 }[/math] und [math]\displaystyle{ f'''(x_0)\neq0 }[/math], dann hat der Graph der Funktion [math]\displaystyle{ f }[/math] an der Stelle [math]\displaystyle{ x_0 }[/math] einen Wendepunkt. Gilt [math]\displaystyle{ f'''(x_0)\gt 0 }[/math], hat der Graph bei [math]\displaystyle{ x_0 }[/math] eine Rechts-Linkskrümmung. Gilt [math]\displaystyle{ f'''(x_0)\lt 0 }[/math], hat der Graph bei [math]\displaystyle{ x_0 }[/math] eine eine Links-Rechtskrümmung.
Funktionswert berechnen
Erfüllt ein [math]\displaystyle{ x_0 \in \mathbb{D}_f }[/math] die notwendige und die hinreichende Bedingung, dann ist [math]\displaystyle{ x_0 }[/math] eine Wendestelle. Der Funktionswert wird dann durch [math]\displaystyle{ f(x_0) }[/math] berechnet.
Beispiele
Kurvenübergänge graphisch erläutert
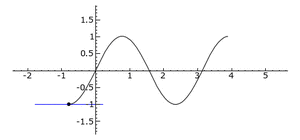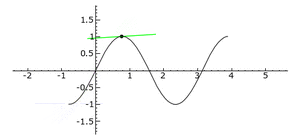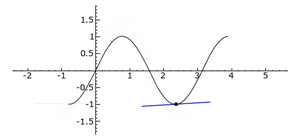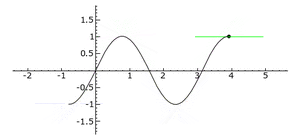
Im Bild auf der rechten Seite ist die Tangente während der Linkskurve blau und während der Rechtskurve grün gefärbt. Die Wendepunkte befinden sich an den Punkten, in denen die Tangente die Farbe wechselt.
Wendepunkt für eine ganzrationale Funktion berechnen
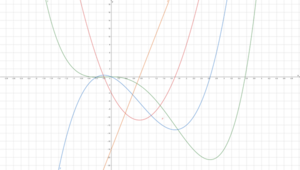
Wir betrachten [math]\displaystyle{ f\left(x\right)=x^4-3x^3-2x^2 }[/math] mit den Ableitungen [math]\displaystyle{ f'\left(x\right)={4x}^3-9x^2-4x }[/math], [math]\displaystyle{ f''\left(x\right)={12x}^2-18x-4 }[/math] und [math]\displaystyle{ f'''\left(x\right)=24x-18 }[/math].
1. Notwendige Bedingung:
[math]\displaystyle{ f''(x)=0 }[/math]
[math]\displaystyle{ 12x^2-18x-4=0 }[/math]
[math]\displaystyle{ x_0\approx 1,696,~x_1\approx -0,196 }[/math]
2. Hinreichende Bedingung:
[math]\displaystyle{ f'''(1,696) \approx 22,704 }[/math] und [math]\displaystyle{ f'''(-0,196) \approx -22,704 }[/math]
Also geht an der Stelle [math]\displaystyle{ x_0 }[/math] der Graph von einer Rechtskrümmung in eine Linkskrümmung über. Bei [math]\displaystyle{ x_1 }[/math] geht der Graph von einer Linkskrümmung in eine Rechtskrümmung über.
3. Funktionswert berechnen:
[math]\displaystyle{ f(1,696)\approx-12,121 }[/math] und [math]\displaystyle{ f(x_1)\approx-0,052 }[/math]
[math]\displaystyle{ f }[/math] die Wendepunkte [math]\displaystyle{ W_0(1,696|-12,121) }[/math] und [math]\displaystyle{ W_1(-0,196|-0,052) }[/math].
Sattelpunkt
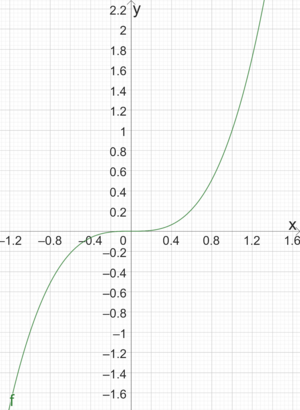
Wir betrachten die Funktion [math]\displaystyle{ f(x)=x^3 }[/math] mit [math]\displaystyle{ f'(x)=3x^2,~f''(x)=6x,~f'''(x)=6~ }[/math].
1. Notwendige Bedingung:
[math]\displaystyle{ f''(x)=0 }[/math]
[math]\displaystyle{ 6x=0 }[/math]
[math]\displaystyle{ x=0 }[/math]
2. Hinreichende Bedingung:
[math]\displaystyle{ f'''(0)=6\gt 0 }[/math]
Der Graph von [math]\displaystyle{ f }[/math] geht bei [math]\displaystyle{ x=0 }[/math] von einer Rechtskrümmung in eine Linkskrümmung über.
3. Funktionswert berechnen:
[math]\displaystyle{ f(0)=0 }[/math]
[math]\displaystyle{ f }[/math] den Wendepunkt [math]\displaystyle{ W(0|0) }[/math]
Außerdem ist [math]\displaystyle{ W }[/math] ein Sattelpunkt, da [math]\displaystyle{ f'(0)=3 \cdot 0^2 =0 }[/math] gilt. Die notwendige Bedingung für Extremwerte ist also ebenfalls erfüllt. Die Steigung in [math]\displaystyle{ W }[/math] ist [math]\displaystyle{ 0 }[/math].