Exponentialfunktion: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| Zeile 10: | Zeile 10: | ||
==Beispiele== | ==Beispiele== | ||
=== | ===Exponentialfunktionen mit verschiedenen Basen=== | ||
Eine [[lineare Funktion]] der Form <math>f(x)=mx+b</math> ist eine ganzrationale Funktion. Der Funktionsterm lässt sich auch als <math>mx^1+b</math> schreiben und ist damit ein Polynom mit dem Grad <math>1</math>. Die Koeffizienten sind <math>m, b</math>. | Eine [[lineare Funktion]] der Form <math>f(x)=mx+b</math> ist eine ganzrationale Funktion. Der Funktionsterm lässt sich auch als <math>mx^1+b</math> schreiben und ist damit ein Polynom mit dem Grad <math>1</math>. Die Koeffizienten sind <math>m, b</math>. | ||
=== | ===Exponentialfunktionen mit verschiedenen === | ||
Die [[quadratische Funktion]] <math>f(x)=-2x^2+3x+5</math> ist eine ganzrationale Funktion mit Grad <math>2</math> und den Koeffizienten <math>-2,3,5</math>. | Die [[quadratische Funktion]] <math>f(x)=-2x^2+3x+5</math> ist eine ganzrationale Funktion mit Grad <math>2</math> und den Koeffizienten <math>-2,3,5</math>. | ||
===Ganzrationale Funktion 3. Grades=== | ===Ganzrationale Funktion 3. Grades=== | ||
Version vom 21. August 2024, 20:18 Uhr
Exponentialfunktionen haben die Form [math]\displaystyle{ f(x)=c \cdot a^x }[/math] und spielen insbesondere in Wachstumsprozessen eine wichtige Rolle. Dazu gehören der Zinseszinseffekt, der Bevölkerungswachstum oder die Ausbreitung von Infektionskrankheiten.
Definition
Eine Funktion der Form [math]\displaystyle{ f(x)=c \cdot a^x }[/math] mit [math]\displaystyle{ c \in \mathbb{R},~a \geq 0,~a \neq 1 }[/math] heißt allgemeine Exponentialfunktion zur Basis a.
[math]\displaystyle{ c }[/math] ist der y-Achsenabschnitt. Der Schnittpunkt mit der y-Achse ist [math]\displaystyle{ S_y(0|c) }[/math]. Gilt [math]\displaystyle{ a\gt 1 }[/math] und [math]\displaystyle{ c\gt 0 }[/math] steigt der Graph streng monoton an. Wir nennen das positives Wachstum. Gilt [math]\displaystyle{ 0\lt a\lt 1 }[/math] und [math]\displaystyle{ c\gt 0 }[/math] fällt der Graph streng monoton. Wir nennen das negatives Wachstum.
Nullstellen
Eine allgemeine Exponentialfunktion zur Basis [math]\displaystyle{ a }[/math] der Form [math]\displaystyle{ f(x)=c \cdot a^x }[/math] mit [math]\displaystyle{ c \in \mathbb{R},~a \geq 0,~a \neq 1 }[/math] hat keine Nullstellen.
Beispiele
Exponentialfunktionen mit verschiedenen Basen
Eine lineare Funktion der Form [math]\displaystyle{ f(x)=mx+b }[/math] ist eine ganzrationale Funktion. Der Funktionsterm lässt sich auch als [math]\displaystyle{ mx^1+b }[/math] schreiben und ist damit ein Polynom mit dem Grad [math]\displaystyle{ 1 }[/math]. Die Koeffizienten sind [math]\displaystyle{ m, b }[/math].
Exponentialfunktionen mit verschiedenen
Die quadratische Funktion [math]\displaystyle{ f(x)=-2x^2+3x+5 }[/math] ist eine ganzrationale Funktion mit Grad [math]\displaystyle{ 2 }[/math] und den Koeffizienten [math]\displaystyle{ -2,3,5 }[/math].
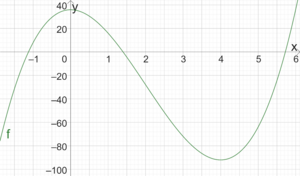
Ganzrationale Funktion 3. Grades
[math]\displaystyle{ f(x)=4x^3-24x^2+36 }[/math] ist eine ganzrationale Funktion, da der Funktionsterm, [math]\displaystyle{ 4x^3-24x^2+36 }[/math], ein Polynom ist. Der Grad von [math]\displaystyle{ f }[/math] ist [math]\displaystyle{ 3 }[/math]. Die Koeffizienten sind [math]\displaystyle{ 3, -2, 0, 36 }[/math]. Der Graph sieht wie folgt aus: