Marktgleichgewicht

Unter vollständiger Konkurrenz passt sich der Preis für ein Gut so an, dass zwischen Angebot und Nachfrage ein Gleichgewischt herrscht. Das Marktgleichgewicht gibt an, für welchen Preis und für welche Menge das Gleichgewicht eintritt.

Definition

Gegeben sei ein Polypol unter vollständiger Konkurrenz, das durch eine Nachfragefunktion [math]\displaystyle{ p_N:\mathbb{D}_{ök} \rightarrow \mathbb{W}_{p_N} }[/math] und eine Angebotsfunktion [math]\displaystyle{ p_A:\mathbb{D}_{ök} \rightarrow \mathbb{W}_{p_A} }[/math] modelliert wird. Der Schnittpunkt [math]\displaystyle{ MGW(x_m|p_A(x_m)) }[/math] bzw. [math]\displaystyle{ MGW(x_m|p_N(x_m)) }[/math] von [math]\displaystyle{ p_N }[/math] und [math]\displaystyle{ p_A }[/math] heißt Marktgleichgewicht. [math]\displaystyle{ x_m }[/math] heißt Gleichgewichtsmenge und [math]\displaystyle{ p_N(x_m) }[/math] bzw. [math]\displaystyle{ p_A(x_m) }[/math] heißt Gleichgewichtspreis oder Marktpreis.

Angebotsüberschuss

Liegt der Preis über dem Gleichgewichtspreis, ist die angebotene Menge [math]\displaystyle{ x_A \in \mathbb{D}_{ök} }[/math] größer als die nachgefragte Menge [math]\displaystyle{ x_N \in \mathbb{D}_{ök} }[/math]. Der Angebotsüberschuss ist dann [math]\displaystyle{ x_A-x_N }[/math].

Nachfrageüberschuss

Liegt der Preis unter dem Gleichgewichtspreis, ist die nachgefragte Menge [math]\displaystyle{ x_N \in \mathbb{D}_{ök} }[/math] größer als die angebotene Menge [math]\displaystyle{ x_A \in \mathbb{D}_{ök} }[/math]. Der Nachfrageüberschuss ist dann [math]\displaystyle{ x_N-x_A }[/math].

Beispiele

Marktgleichgewicht berechnen

Marktgleichgewicht für [math]\displaystyle{ p_N(x)=-2x+10 }[/math] und [math]\displaystyle{ p_A(x)=\frac{2}{3}x+2 }[/math]

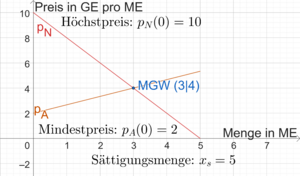
Wir betrachten den Ölmarkt. Da wir viele Anbieter haben und niemand den Marktpreis beeinflussen kann, handelt es sich um ein Polypol unter vollständiger Konkurrenz. Wir gehen davon aus, dass die Nachfrage nach Öl am meisten vom Preis beeinflusst wird. Das Gesetz der Nachfrage besagt, dass die Nachfrage nach Öl sinkt, wenn der Preis steigt. Außerdem steigt gemäß dem Gesetz des Angebots das Angebot mit dem Preis. Den Zusammenhang können wir mathematisch modellieren. [math]\displaystyle{ y }[/math] bezeichnet den Preis pro ME in GE und [math]\displaystyle{ x }[/math] bezeichnet die Menge an Öl in ME. Die Nachfragefunktion ist

• [math]\displaystyle{ p_N(x)=-2x+10 }[/math]

und die Angebotsfunktion ist

• [math]\displaystyle{ p_A(x)=\frac{2}{3}x+2 }[/math].

Die Abbildung zeigt die Graphen der Funktionen. Der ökonomische Definitionsbereich ist [math]\displaystyle{ \mathbb{D}_{\text{ök}}=[0;5] }[/math]. Wir berechnen das Marktgleichgewicht:

[math]\displaystyle{ p_N(x)=p_A(x) }[/math]
[math]\displaystyle{ -2x+10=\frac{2}{3}x+2~|~-2 }[/math]
[math]\displaystyle{ -2x+8=\frac{2}{3}x~|~+2x }[/math]
[math]\displaystyle{ 8=\frac{8}{3}x~|~:\frac{8}{3} }[/math]
[math]\displaystyle{ 3=x }[/math]

Die Gleichgewichtsmenge beträgt [math]\displaystyle{ x=3 }[/math] ME. Der Gleichgewichtspreis beträgt [math]\displaystyle{ p_N(3)=-2 \cdot 3+10=4 }[/math] GE pro ME. Das Marktgleichgewicht ist [math]\displaystyle{ MGW(3|4) }[/math].

Angebots- und Nachfrageüberschuss berechnen

Der Preis