Langfristige Preisuntergrenze: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
Es sei <math>K: \mathbb{D}_{ök} \rightarrow \mathbb{W}_{K}</math> eine [[Kostenfunktion]] und <math>k</math> die dazugehörige Stückkostenfunktion. Die [[Extremwert#Definition|Minimalstelle]] <math>x_0 \in \mathbb{D}_{ök}</math> der Stückkosten <math>k</math> nennen wir '''Betriebsoptimum'''. Das dazugehörige [[Extremwert#Definition|Minimum]] <math>k(x_0)</math> heißt '''langfristige Preisuntergrenze'''. | Es sei <math>K: \mathbb{D}_{ök} \rightarrow \mathbb{W}_{K}</math> eine [[Kostenfunktion]] und <math>k</math> die dazugehörige Stückkostenfunktion. Die [[Extremwert#Definition|Minimalstelle]] <math>x_0 \in \mathbb{D}_{ök}</math> der Stückkosten <math>k</math> nennen wir '''Betriebsoptimum'''. Das dazugehörige [[Extremwert#Definition|Minimum]] <math>k(x_0)</math> heißt '''langfristige Preisuntergrenze'''. | ||
<html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/x8k9v9Dg7yY?si=WH-RKwNoiQjw5YD9" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | <html> | ||
<iframe width="280" height="157.5" src="https://www.youtube.com/embed/RywM3XEzgWo?si=woHR5oYGNCes6Tmd" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" referrerpolicy="strict-origin-when-cross-origin" allowfullscreen></iframe> | |||
<iframe width="280" height="157.5" src="https://www.youtube.com/embed/JeLufqynqKU?si=NOL6WB7VjozoVbni" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" referrerpolicy="strict-origin-when-cross-origin" allowfullscreen></iframe> | |||
<iframe width="280" height="157.5" src="https://www.youtube.com/embed/x8k9v9Dg7yY?si=WH-RKwNoiQjw5YD9" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | |||
==Gewinn im Betriebsoptimum== | ==Gewinn im Betriebsoptimum== | ||
| Zeile 14: | Zeile 17: | ||
==Beispiele== | ==Beispiele== | ||
===Stückkosten für die allgemeine Kostenfunktion dritten Grades=== | ===Stückkosten für die allgemeine Kostenfunktion dritten Grades=== | ||
Die Kostenfunktion sei durch <math>K(x)=ax^3+bx^2+cx+d</math> mit <math>a, b, c, d \in \mathbb{R}^{\neq\ 0}</math> gegeben. Wir berechnen die Stückkosten durch <math>k(x)=\frac{K(x)}{x}=\frac{ax^3+bx^2+cx+d}{x}=ax^2+bx+c+\frac{d}{x}</math>. Die Kostenfunktion lässt sich mit den Stückkosten durch <math>K(x)=k(x)\cdot x=(ax^3+bx^2+cx+\frac{d}{x})\cdot x=ax^3+bx^2+cx+d</math> berechnen. | Die Kostenfunktion sei durch <math>K(x)=ax^3+bx^2+cx+d</math> mit <math>a, b, c, d \in \mathbb{R}^{\neq\ 0}</math> gegeben. Wir berechnen die Stückkosten durch <math>k(x)=\frac{K(x)}{x}=\frac{ax^3+bx^2+cx+d}{x}=ax^2+bx+c+\frac{d}{x}=ax^2+bx+c+d\cdot x^{-1}</math>. Die Kostenfunktion lässt sich mit den Stückkosten durch <math>K(x)=k(x)\cdot x=(ax^3+bx^2+cx+\frac{d}{x})\cdot x=ax^3+bx^2+cx+d</math> berechnen. | ||
===Betriebsoptimum und langfristige Preisuntergrenze graphisch ermitteln=== | ===Betriebsoptimum und langfristige Preisuntergrenze graphisch ermitteln=== | ||
| Zeile 34: | Zeile 37: | ||
[[Kategorie:Differentialrechnung]] | [[Kategorie:Differentialrechnung]] | ||
[[Kategorie:Gewinnanalyse]] | [[Kategorie:Gewinnanalyse]] | ||
[[Kategorie: | [[Kategorie:FHR_WuV_Mathe]] | ||
[[Kategorie:AHR_WuV_Mathe_GK]] | |||
Aktuelle Version vom 3. Dezember 2025, 14:32 Uhr
Um Marktanteile zurückzugewinnen bzw. mehr Einheiten eines Produkts zu verkaufen, wird der Verkaufspreis für das Produkt gesenkt. Die langfristige Preisuntergrenze ist der Verkaufspreis, bei dem wir einen Gewinn von 0 GE erzielen. Dieser Verkaufspreis kann langfristig gehalten werden, da der Erlös die Kosten deckt. Die dazugehörige Produktionsmenge ist das Betriebsoptimum.
Stückkostenfunktion
Gegeben sei eine Kostenfunktion [math]\displaystyle{ K: \mathbb{D}_{ök} \rightarrow \mathbb{W}_{K} }[/math]. Dann nennen wir [math]\displaystyle{ k(x)=\frac{K(x)}{x} }[/math] Stückkostenfunktion oder Stückkosten. Die Kostenfunktion berechnet sich durch [math]\displaystyle{ K(x)=k(x)\cdot x }[/math]. [math]\displaystyle{ x }[/math] ist in ME, [math]\displaystyle{ K(x) }[/math] in GE und [math]\displaystyle{ k_v(x) }[/math] in GE pro ME gegeben.
Definition
Es sei [math]\displaystyle{ K: \mathbb{D}_{ök} \rightarrow \mathbb{W}_{K} }[/math] eine Kostenfunktion und [math]\displaystyle{ k }[/math] die dazugehörige Stückkostenfunktion. Die Minimalstelle [math]\displaystyle{ x_0 \in \mathbb{D}_{ök} }[/math] der Stückkosten [math]\displaystyle{ k }[/math] nennen wir Betriebsoptimum. Das dazugehörige Minimum [math]\displaystyle{ k(x_0) }[/math] heißt langfristige Preisuntergrenze.
Gewinn im Betriebsoptimum
Ist der Verkaufspreis für ein Produkt die langfristige Preisuntergrenze und wird das Betriebsoptimum an Mengeneinheiten verkauft, decken sich die Kosten und der Erlös und es fällt ein Gewinn von 0 Geldeinheiten an. Der Preis kann damit langfristig, also auf Dauer gehalten werden.
Beispiele
Stückkosten für die allgemeine Kostenfunktion dritten Grades
Die Kostenfunktion sei durch [math]\displaystyle{ K(x)=ax^3+bx^2+cx+d }[/math] mit [math]\displaystyle{ a, b, c, d \in \mathbb{R}^{\neq\ 0} }[/math] gegeben. Wir berechnen die Stückkosten durch [math]\displaystyle{ k(x)=\frac{K(x)}{x}=\frac{ax^3+bx^2+cx+d}{x}=ax^2+bx+c+\frac{d}{x}=ax^2+bx+c+d\cdot x^{-1} }[/math]. Die Kostenfunktion lässt sich mit den Stückkosten durch [math]\displaystyle{ K(x)=k(x)\cdot x=(ax^3+bx^2+cx+\frac{d}{x})\cdot x=ax^3+bx^2+cx+d }[/math] berechnen.
Betriebsoptimum und langfristige Preisuntergrenze graphisch ermitteln
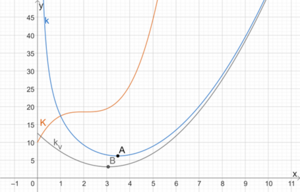
Bei den folgenden Werten wurde gerundet. Der Punkt [math]\displaystyle{ A(3,48|6,17) }[/math] ist Tiefpunkt von [math]\displaystyle{ k }[/math] und damit ist das Betriebsoptimum bei ca. [math]\displaystyle{ 3,48~ME }[/math] und die langfristige Preisuntergrenze bei ca. [math]\displaystyle{ 6,17~ \frac{GE}{ME} }[/math].
Betriebsoptimum und langfristige Preisuntergrenze berechnen
Die Gesamtkostenfunktion für ein Produkt sei durch [math]\displaystyle{ K(x)=x^3-6,125x^2+12,5x+10 }[/math] gegeben. [math]\displaystyle{ x }[/math] ist in ME und [math]\displaystyle{ K(x) }[/math] in GE.
Wir berechnen die Stückkosten [math]\displaystyle{ k(x)=\frac{x^3-6,125x^2+12,5x+10}{x}=x^2-6,125x+12,5+\frac{10}{x}=x^2-6,125x+12,5+10x^{-1} }[/math] mit [math]\displaystyle{ k'(x)=2x-6,125-10x^{-2}=2x-6,125-\frac{10}{x^2} }[/math] und [math]\displaystyle{ k''(x)=2+20x^{-3}=2+\frac{20}{x^3} }[/math].
- Notwendige Bedingung:
[math]\displaystyle{ k'(x)=0 }[/math]
[math]\displaystyle{ 2x-6,125-\frac{10}{x^2}=0~|~\cdot x^2 }[/math]
[math]\displaystyle{ 2x^3-6,125x^2-10=0 }[/math]
Lösen mit dem Taschenrechner ergibt [math]\displaystyle{ xx \approx 3,48 }[/math] - Hinreichende Bedingung:
[math]\displaystyle{ k''(3,48)=2+\frac{20}{3,48^3}\approx 2,48 \gt 0 }[/math], daher beträgt das Betriebsoptimum [math]\displaystyle{ x\approx 3,48 }[/math] ME. - Funktionswert ermitteln:
[math]\displaystyle{ k(3,48)=3,48^2-6,125 \cdot 3,48 +12,5+\frac{10}{3,48} \approx 6,17 \frac{GE}{ME} }[/math] ist die langfristige Preisuntergrenze.
Gewinn im Betriebsoptimum ermitteln
Wir führen das vorherige Beispiel fort. Die langfristige Preisuntergrenze ist der neue Verkaufspreis für das Produkt. Damit ist die Erlösfunktion [math]\displaystyle{ E(x)=6,17x }[/math]. Die Gewinnfunktion ist dann [math]\displaystyle{ G(x)=E(x)-K(x)=6,17x-(x^3-6,125x^2+12,5x+10)=6,17x-x^3+6,125x^2-12,5x-10=-x^3+6,125x^2-6,33x-10 }[/math]. Produzieren wir das Betriebsoptimum, also [math]\displaystyle{ x\approx 3,48 }[/math] ME, beträgt der Gewinn [math]\displaystyle{ G(3,48)=-(3,48)^3+6,125 \cdot 3,48^2-6,33 \cdot 3,48-10 \approx 0 }[/math] GE.