Natürliche Exponentialfunktion: Unterschied zwischen den Versionen

← Zum vorherigen Versionsunterschied

VisuellWikitext

@@ Zeile 2: / Zeile 2: @@
 ==Euler'sche Zahl e==
-Die Euler'sche Zahl ist <math>e \approx 2,71828... </math>.
+Die '''Euler'sche Zahl''' ist <math>e \approx 2,71828...</math>.
 ==Herleitung der Euler'schen Zahl e==
-Wir verwenden, dass die [[Exponentialfunktion#Ableitung|Ableitung]] einer Exponentialfunktion der Form <math>f(t)=a^t</math> durch <math>f'(t)=ca^t</math> gegeben ist. Wir setzen <math>c=1</math> und ermitteln eine Basis <math>a</math>, so dass <math> f(t)=a^t </math> die Ableitung <math>f'(t)=a^t</math> hat:
+Wir verwenden, dass die [[Exponentialfunktion#Ableitung|Ableitung]] einer Exponentialfunktion der Form <math>f(x)=a^x</math> durch <math>f'(x)=ca^x</math> gegeben ist. Wir setzen <math>c=1</math> und ermitteln eine Basis <math>a</math>, so dass <math> f(x)=a^x </math> die Ableitung <math>f'(x)=a^x</math> hat:
 <math> c=1</math>
@@ Zeile 19: / Zeile 19: @@
 <math>a \approx \sqrt[h]{h+1} </math>
-Lassen wir <math>h</math> gegen 0 laufen, erhalten wir <math>a \approx 2,71828... </math>.
+Lassen wir <math>h</math> gegen 0 laufen, erhalten wir <math>a \approx 2,71828... </math>. Dies ist die Euler'sche Zahl <math>e</math>.
-Diese Zahl heißt Euler'sche Zahl <math>e</math>. Die Funktion <math>f(x)=e^x</math> heißt natürliche Exponentialfunktion oder e-Funktion.
+==Definition==
+Die [[Funktion]] <math>f:\mathbb{D}_f \rightarrow \mathbb{R}</math> der Form <math>f(x)=e^x</math> mit der Euler'schen Zahl <math>e</math> heißt '''natürliche Exponentialfunktion''' oder '''e-Funktion''' und hat die [[Ableitung]] <math>f'(x)=e^x</math>.
-==Definition==
+==Erweiterte Form==
+Eine [[Funktion]] <math>f:\mathbb{D}_f \rightarrow \mathbb{R}</math> der Form <math>f(x)=c \cdot e^{\lambda x}+d</math> mit <math>a,~c,~d,~\lambda \in \mathbb{R},~a \geq 0,~a \neq 1</math> heißt '''erweiterte e-Funktion'''. .
+==Beispiele==
+===Graphen von e-Funktionen===
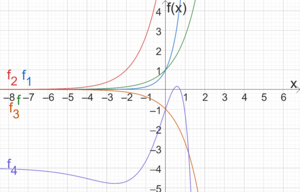
+[[Datei:E-FunktionGraphen1.png|mini|Graphen von <math>f(x)=e^x</math>,<math>f_1(x)=e^{2x}</math>, <math>f_2(x)=e^{x+2}</math>, <math>f_3(x)=-e^x</math>, <math>f_4(x)=(-2x^2+3)e^x-4</math>]]
+Auf der rechten Seite sehen wir die Graphen einer e-Funktion und von e-Funktionen in erweiterter Form. <math>f</math> zeigt die e-Funktion. <math>f_1</math> verläuft im Vergleich zu <math>f</math> steiler. Schiebt man <math>f</math> um zwei Stellen nach rechts, erhält man <math>f_2</math>. Wird <math>f</math> an der x-Achse gespiegelt, erhalten wir <math>f_3</math>. <math>f_4</math> entsteht aus <math>f</math>, indem der Graph abschnittsweise die Form des Polynoms <math>-2x^2+3</math> annimmt und für <math>x</math> gegen <math>- \infty</math> <math>y=4</math> als Asymptote hat.
+===Ableitungen von e-Funktionen===
+Wir bilden die Ableitungen von <math>f,g,h</math>:
+*<math>f(x)=e^x</math>
+**<math>f'(x)=e^x</math>
+**<math>f''(x)=e^x</math>
+*<math>g(x)=e^x-3x^2+3</math>
+**<math>g'(x)=e^x-6x</math>
+**<math>g''(x)=e^x-6</math>
+*<math>h(x)=(-2)e^x-3x^4+3x</math>
+**<math>h'(x)=(-2)e^x-12x^3+3</math>
+**<math>h''(x)=e^x-36x^2</math>
+[[Kategorie:Mathematische Funktion]]
+[[Kategorie:AHR_WuV_Mathe_GK]]