Nullstelle: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 61: | Zeile 61: | ||
===Quadratische Funktion=== | ===Quadratische Funktion=== | ||
Die | Die Nullstellen einer quadratischen Funktion <math>{f\left(x\right)=x}^2+px+q</math> werden durch Auflösen der Gleichung <math>x^2+px+q=0</math> nach <math>x</math> ausgerechnet. Die Lösung der Gleichung wird mit der '''p-q-Formel''', <math>x=-\frac{p}{2}\pm\sqrt{\left(\frac{p}{2}\right)^2-q}</math>, berechnet. Ist der Wert unter der Wurzel negativ, existiert keine Nullstelle. Ist der Wert unter der Wurzel 0 existiert genau eine Nullstelle und ansonsten existieren zwei Nullstellen. | ||
====pq-Formel anwenden==== | ====pq-Formel anwenden==== | ||
[[Datei:QuadratischeFunktionenBeispielQuadFktNST.png|mini|Graph der Funktion <math>f(x)=2x^2+8x+4</math> mit Nullstellen]] | [[Datei:QuadratischeFunktionenBeispielQuadFktNST.png|mini|Graph der Funktion <math>f(x)=2x^2+8x+4</math> mit Nullstellen]] | ||
Wir betrachten <math> | Wir betrachten <math>f(x)=2x^2+8x+4</math>. Wir rechnen | ||
<math>{2x}^2+8x+4=0 | <math>{2x}^2+8x+4=0~|~ :2 </math> | ||
<math>x^2+4x+2=0\ </math> | <math>x^2+4x+2=0\ </math> | ||
| Zeile 80: | Zeile 80: | ||
<html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/62W7vkZOsgY?si=OQN3whbksaE9jebQ" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | <html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/62W7vkZOsgY?si=OQN3whbksaE9jebQ" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | ||
=== | ====Nullstellen ohne pq-Formel berechnen==== | ||
Einige Nullstellen bzw. Lösungen von quadratischen Gleichungen können auch ohne p-q-Formel bestimmt werden: | Einige Nullstellen bzw. Lösungen von quadratischen Gleichungen können auch ohne p-q-Formel bestimmt werden: | ||
| Zeile 113: | Zeile 113: | ||
<html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/YP3qpsTryrc?si=d2H0Gbv2T4DTI0px" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | <html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/YP3qpsTryrc?si=d2H0Gbv2T4DTI0px" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | ||
===Herleitung p-q-Formel (nur zur Vertiefung)=== | ====Herleitung der p-q-Formel (nur zur Vertiefung)==== | ||
Um die Nullstellen einer beliebigen quadratischen Funktion <math>f\left(x\right)=ax^2+bx+c</math> zu bestimmen, rechnet man: | Um die Nullstellen einer beliebigen quadratischen Funktion <math>f\left(x\right)=ax^2+bx+c</math> zu bestimmen, rechnet man: | ||
| Zeile 134: | Zeile 134: | ||
<math>x=-\frac{b}{2}\pm\sqrt{{(\left(\frac{b}{2}\right)}^2-c)}</math> | <math>x=-\frac{b}{2}\pm\sqrt{{(\left(\frac{b}{2}\right)}^2-c)}</math> | ||
[[Kategorie: | [[Kategorie:Mathematische Funktion]] | ||
[[Kategorie:FHR_WuV_Mathe]] | |||
Aktuelle Version vom 21. Juli 2024, 10:19 Uhr
Nullstellen sind die [math]\displaystyle{ x }[/math]-Werte, bei denen der Graph die [math]\displaystyle{ x }[/math]-Achse schneidet oder berührt.
Definition
Die Nullstellen einer Funktion sind diejenigen Werte im Definitionsbereich, für die der Funktionswert gleich null ist. In einem Koordinatensystem entsprechen diese Werte den Schnitt- oder Berührungsstellen des Funktionsgraphen mit der x-Achse. Eine Funktion [math]\displaystyle{ f: \mathbb{D} \rightarrow \mathbb{W} }[/math] hat eine Nullstelle bei [math]\displaystyle{ x_0 \in \mathbb{D} }[/math], wenn [math]\displaystyle{ f(x_0)=0 }[/math] gilt.
Für eine Nachfragefunktion wird die positive Nullstelle auch Sättigungsmenge genannt.
Beispiele
Lineare Funktion
Für eine lineare Funktion [math]\displaystyle{ f }[/math] mit [math]\displaystyle{ f(x)=mx+b }[/math] wird die Nullstelle berechnet, indem [math]\displaystyle{ f(x)=0 }[/math] eingesetzt und nach [math]\displaystyle{ x }[/math] umgeformt wird:
[math]\displaystyle{ f(x)=mx+b }[/math]
[math]\displaystyle{ 0=mx+b\ ~|~-b }[/math]
[math]\displaystyle{ -b=\ mx ~|~ : m }[/math]
[math]\displaystyle{ -\frac{b}{m}= x }[/math] ist die Nullstelle.
Nullstellenberechnung für eine konkrete Funktionsvorschrift
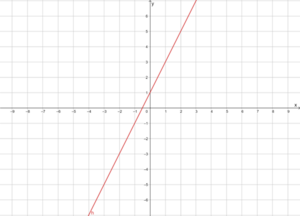
Gegeben ist die lineare Funktion
[math]\displaystyle{ f(x)=2x+1 }[/math]
Setzt man [math]\displaystyle{ f(x)=0 }[/math] ein, folgt
[math]\displaystyle{ 0=2x+1~|~-1 }[/math]
[math]\displaystyle{ -1=\ 2x~|~:2 }[/math]
[math]\displaystyle{ -\frac{1}{2}=\ x }[/math] ist die Nullstelle.
Lineare Funktion ohne Nullstelle
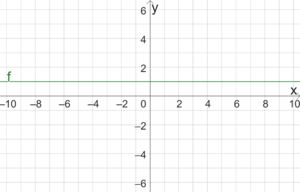
Gegeben ist die lineare Funktion
[math]\displaystyle{ f(x)=0x+1 }[/math]
Die Steigung ist 0 und der y-Achsenabschnitt ist 1. Berechnen wir die Nullstelle, erhalten wir:
[math]\displaystyle{ 0=0x+1 }[/math]
[math]\displaystyle{ 0 = 1 }[/math]
Das ist ein Widerspruch, da [math]\displaystyle{ 0\neq 1 }[/math] ist. Die lineare Funktion hat also keine Nullstelle. Dies erkennt man auch am Graphen der Funktion, da dieser parallel zur [math]\displaystyle{ x }[/math]-Achse verläuft und damit keine Nullstellen hat.
Lineare Funktion mit unendlich vielen Nullstellen
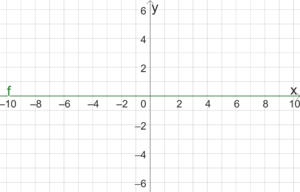
Gegeben ist die lineare Funktion
[math]\displaystyle{ f(x)=0x+0 }[/math]
Die Steigung ist 0 und der y-Achsenabschnitt ist 0. Berechnen wir die Nullstellen, erhalten wir:
[math]\displaystyle{ 0=0x+0 }[/math]
[math]\displaystyle{ 0= 0 }[/math]
Die Aussage ist wahr, also ist jeder [math]\displaystyle{ x }[/math]-Wert eine Nullstelle von [math]\displaystyle{ f }[/math]. Der Graph verläuft vollständig auf der x-Achse.
Quadratische Funktion
Die Nullstellen einer quadratischen Funktion [math]\displaystyle{ {f\left(x\right)=x}^2+px+q }[/math] werden durch Auflösen der Gleichung [math]\displaystyle{ x^2+px+q=0 }[/math] nach [math]\displaystyle{ x }[/math] ausgerechnet. Die Lösung der Gleichung wird mit der p-q-Formel, [math]\displaystyle{ x=-\frac{p}{2}\pm\sqrt{\left(\frac{p}{2}\right)^2-q} }[/math], berechnet. Ist der Wert unter der Wurzel negativ, existiert keine Nullstelle. Ist der Wert unter der Wurzel 0 existiert genau eine Nullstelle und ansonsten existieren zwei Nullstellen.
pq-Formel anwenden
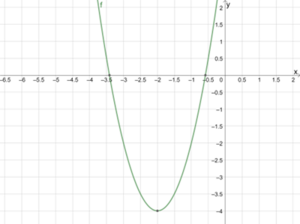
Wir betrachten [math]\displaystyle{ f(x)=2x^2+8x+4 }[/math]. Wir rechnen
[math]\displaystyle{ {2x}^2+8x+4=0~|~ :2 }[/math]
[math]\displaystyle{ x^2+4x+2=0\ }[/math]
damit wir die p-q-Formel anwenden können. Es gilt [math]\displaystyle{ p=4 }[/math] und [math]\displaystyle{ q=2 }[/math]. Diese Werte können wir einsetzen: [math]\displaystyle{ x_1=-\frac{4}{2}+\sqrt{\left(\frac{4}{2}\right)^2-2}=-2-\sqrt2\approx-3,41 }[/math] und [math]\displaystyle{ x_2=-\frac{4}{2}+\sqrt{\left(\frac{4}{2}\right)^2-2}=-2+\sqrt2\approx-0,59 }[/math]
Also hat f die Nullstellen [math]\displaystyle{ x_1\approx-3,41 }[/math] und [math]\displaystyle{ x_2\approx-0,59 }[/math]. Das sind die x-Werte, bei denen der Graph die x-Achse schneidet.
Nullstellen ohne pq-Formel berechnen
Einige Nullstellen bzw. Lösungen von quadratischen Gleichungen können auch ohne p-q-Formel bestimmt werden:
Direktes Auflösen einer quadratischen Gleichung nach x:
[math]\displaystyle{ 3\left(x-5\right)^2=27\ |\ \div3 }[/math]
[math]\displaystyle{ \left(x-5\right)^2=9\ |\ \sqrt{~} }[/math]
[math]\displaystyle{ x-5=9\ \vee x-5=-9\ |+5 }[/math]
[math]\displaystyle{ x=14\ \vee x=-4 }[/math]
Produkt von Nullstellen:
[math]\displaystyle{ \left(x-8\right)\left(x+3\right)=0 }[/math]
[math]\displaystyle{ x-8=0\ \vee x-3=0 }[/math]
[math]\displaystyle{ x=8\ \vee x=3 }[/math]
Direktes Auflösen nach x:
[math]\displaystyle{ 7x^2-343=0\ |\ \div7 }[/math]
[math]\displaystyle{ x^2-49=0\ |+49 }[/math]
[math]\displaystyle{ x^2=49\ \ |\ \sqrt{~} }[/math]
[math]\displaystyle{ x=7 \text{ or } x=-7 }[/math]
Herleitung der p-q-Formel (nur zur Vertiefung)
Um die Nullstellen einer beliebigen quadratischen Funktion [math]\displaystyle{ f\left(x\right)=ax^2+bx+c }[/math] zu bestimmen, rechnet man:
[math]\displaystyle{ ax^2+bx+c=0 }[/math]
[math]\displaystyle{ a{(x}^2+\frac{b}{a}x)+c=0 }[/math]
[math]\displaystyle{ a{(x}^2+\frac{b}{a}x)+c=0 }[/math]
[math]\displaystyle{ a{(x}^2+\frac{b}{a}x+\left(\frac{b}{2a}\right)^2-\left(\frac{b}{2a}\right)^2)+c=0 }[/math]
[math]\displaystyle{ a{(x+\frac{b}{2a})}^2-\left(\frac{b}{2}\right)^2+c=0 }[/math]
[math]\displaystyle{ a\left(x+\frac{b}{2a}\right)=\pm\sqrt{\left(\frac{b}{2}\right)^2-c} }[/math]
[math]\displaystyle{ x=-\frac{b}{2a}\pm\sqrt{\frac{1}{a}{(\left(\frac{b}{2}\right)}^2-c)} }[/math]
Gilt [math]\displaystyle{ a=1 }[/math], so erhält man:
[math]\displaystyle{ x=-\frac{b}{2}\pm\sqrt{{(\left(\frac{b}{2}\right)}^2-c)} }[/math]