Monotone Funktion: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „Wir analysieren im Folgenden den Verlauf der Graphen von Funktionen mit Hilfe der Ableitung. ==Definition== Eine Funktion <math>f:\mathbb{D}_f \rightarrow \mathbb{W}_f</math> heißt * '''monoton steigend''', wenn für alle <math>x_1,x_2 \in \mathbb{D}_f</math> mit <math>x_1 < x_2</math> gilt, dass <math>f(x_1) \leq f(x_2)</math> ist. * '''streng monoton steigend''', wenn für alle <math>x_1,x_2 \in \math…“ |
Markierungen: Mobile Bearbeitung Mobile Web-Bearbeitung |
||
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 21: | Zeile 21: | ||
* '''linksgekrümmt''', falls die [[Ableitungsfunktion]] <math>f'</math> in <math>I</math> monoton steigt. | * '''linksgekrümmt''', falls die [[Ableitungsfunktion]] <math>f'</math> in <math>I</math> monoton steigt. | ||
* '''rechtsgekrümmt''', falls die [[Ableitungsfunktion]] <math>f'</math> in <math>I</math> monoton fällt. | * '''rechtsgekrümmt''', falls die [[Ableitungsfunktion]] <math>f'</math> in <math>I</math> monoton fällt. | ||
Wir sprechen auch von '''Links-''' oder '''Rechtskurven''' bzw. '''Rechts-''' oder '''Linkskrümmung'''. | |||
==Degressiv und Progressiv== | |||
Eine Funktion | |||
* wächst '''degressiv''', wenn die Funktion monoton steigt und der Graph rechtsgekrümmt verläuft. | |||
* nimmt '''degressiv''' ab, wenn die Funktion monoton fällt und der Graph linksgekrümmt verläuft. | |||
* wächst '''progressiv''', wenn die Funktion monoton steigt und der Graph linkgsgekrümmt verläuft. | |||
* nimmmt '''progressiv''' ab, wenn die Funktion monoton fällt und der Graph rechtsgekrümmt verläuft. | |||
==Beispiele== | ==Beispiele== | ||
| Zeile 33: | Zeile 42: | ||
Außerdem ist der [[Graph]] von <math>f</math> linksgekrümmt, da <math>f'</math> monoton steigt. Das erkennen wir daran, dass <math>f''(x)=2>0</math> ist. | Außerdem ist der [[Graph]] von <math>f</math> linksgekrümmt, da <math>f'</math> monoton steigt. Das erkennen wir daran, dass <math>f''(x)=2>0</math> ist. | ||
[[Kategorie:Differentialrechnung]] | [[Kategorie:Differentialrechnung]] | ||
[[Kategorie:AHR WuV Mathe GK]] | |||
Aktuelle Version vom 27. September 2024, 07:20 Uhr
Wir analysieren im Folgenden den Verlauf der Graphen von Funktionen mit Hilfe der Ableitung.
Definition
Eine Funktion [math]\displaystyle{ f:\mathbb{D}_f \rightarrow \mathbb{W}_f }[/math] heißt
- monoton steigend, wenn für alle [math]\displaystyle{ x_1,x_2 \in \mathbb{D}_f }[/math] mit [math]\displaystyle{ x_1 \lt x_2 }[/math] gilt, dass [math]\displaystyle{ f(x_1) \leq f(x_2) }[/math] ist.
- streng monoton steigend, wenn für alle [math]\displaystyle{ x_1,x_2 \in \mathbb{D}_f }[/math] mit [math]\displaystyle{ x_1 \lt x_2 }[/math] gilt, dass [math]\displaystyle{ f(x_1) \lt f(x_2) }[/math] ist.
- monoton fallend, wenn für alle [math]\displaystyle{ x_1,x_2 \in \mathbb{D}_f }[/math] mit [math]\displaystyle{ x_1 \lt x_2 }[/math] gilt, dass [math]\displaystyle{ f(x_1) \geq f(x_2) }[/math] ist.
- streng monoton fallend, wenn für alle [math]\displaystyle{ x_1,x_2 \in \mathbb{D}_f }[/math] mit [math]\displaystyle{ x_1 \lt x_2 }[/math] gilt, dass [math]\displaystyle{ f(x_1) \gt f(x_2) }[/math] ist.
- monoton, wenn sie monoton steigt oder fällt.
- streng monoton, wenn sie streng monoton steigt oder fällt.
Monotoniesatz
Eine differenzierbare Funktion [math]\displaystyle{ f:\mathbb{D}_f \rightarrow \mathbb{W}_f }[/math] ist
- monoton steigend, wenn für alle [math]\displaystyle{ x \in \mathbb{D}_f }[/math] gilt, dass [math]\displaystyle{ f'(x)\geq 0 }[/math] ist.
- streng monoton steigend, wenn für alle [math]\displaystyle{ x \in \mathbb{D}_f }[/math] gilt, dass [math]\displaystyle{ f'(x)\gt 0 }[/math] ist.
- monoton fallend, wenn für alle [math]\displaystyle{ x \in \mathbb{D}_f }[/math] gilt, dass [math]\displaystyle{ f'(x) \leq 0 }[/math] ist.
- streng monoton fallend, wenn für alle [math]\displaystyle{ x \in \mathbb{D}_f }[/math] gilt, dass [math]\displaystyle{ f'(x)\lt 0 }[/math] ist.
Krümmung einer Funktion
Die Funktion [math]\displaystyle{ f }[/math] sei an jedem Punkt [math]\displaystyle{ f }[/math] in einem Intervall [math]\displaystyle{ I \subseteq \mathbb{D}_f }[/math] differenzierbar. Der Graph von [math]\displaystyle{ f }[/math] ist auf [math]\displaystyle{ I }[/math]
- linksgekrümmt, falls die Ableitungsfunktion [math]\displaystyle{ f' }[/math] in [math]\displaystyle{ I }[/math] monoton steigt.
- rechtsgekrümmt, falls die Ableitungsfunktion [math]\displaystyle{ f' }[/math] in [math]\displaystyle{ I }[/math] monoton fällt.
Wir sprechen auch von Links- oder Rechtskurven bzw. Rechts- oder Linkskrümmung.
Degressiv und Progressiv
Eine Funktion
- wächst degressiv, wenn die Funktion monoton steigt und der Graph rechtsgekrümmt verläuft.
- nimmt degressiv ab, wenn die Funktion monoton fällt und der Graph linksgekrümmt verläuft.
- wächst progressiv, wenn die Funktion monoton steigt und der Graph linkgsgekrümmt verläuft.
- nimmmt progressiv ab, wenn die Funktion monoton fällt und der Graph rechtsgekrümmt verläuft.
Beispiele
Monotonie einer linearen Funktion
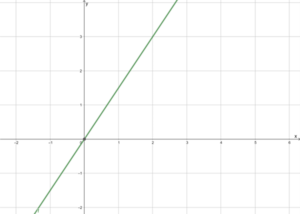
Die Funktion [math]\displaystyle{ f(x)=1,5x+0 }[/math] ist für alle [math]\displaystyle{ x \in \mathbb{R} }[/math] streng monoton steigend, da [math]\displaystyle{ f'(x)=1,5\gt 0 }[/math] gilt. Außerdem ist für beliebige [math]\displaystyle{ x }[/math]-Werte die obige Definition für eine streng monoton steigende Funktion erfüllt. Beispielsweise gilt für [math]\displaystyle{ x_1=1 }[/math] und [math]\displaystyle{ x_2=2 }[/math], dass [math]\displaystyle{ x_1=1\lt 2=x_2 }[/math] und [math]\displaystyle{ f(x_1)=f(1)=1,5\lt 3=f(2)=f(x_2) }[/math] ist. Der Graph von [math]\displaystyle{ f }[/math] steigt folglich im kompletten Definitionsbereich.
Monotonie einer quadratischen Funktion
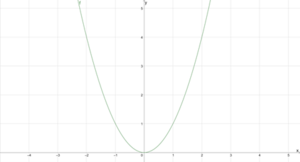
Die Funktion [math]\displaystyle{ f(x)=1,5x+0 }[/math] ist für alle [math]\displaystyle{ x \in \mathbb{R}^{\gt 0} }[/math] streng monoton steigend und für alle [math]\displaystyle{ x \in \mathbb{R}^{\lt 0} }[/math] streng monoton fallend. Für die Ableitungsfunktion gilt [math]\displaystyle{ f'(x)=2x }[/math]. [math]\displaystyle{ f' }[/math] nimmt positive Funktionswerte für positive [math]\displaystyle{ x }[/math]-Werte an und negative Funktionswerte für negative [math]\displaystyle{ x }[/math]-Werte an.
Außerdem ist der Graph von [math]\displaystyle{ f }[/math] linksgekrümmt, da [math]\displaystyle{ f' }[/math] monoton steigt. Das erkennen wir daran, dass [math]\displaystyle{ f''(x)=2\gt 0 }[/math] ist.