Nullstelle
Nullstellen sind die [math]\displaystyle{ x }[/math]-Werte, bei denen der Graph die [math]\displaystyle{ x }[/math]-Achse schneidet oder berührt.
Definition
Die Nullstellen einer Funktion sind diejenigen Werte im Definitionsbereich, für die der Funktionswert gleich null ist. In einem Koordinatensystem entsprechen diese Werte den Schnitt- oder Berührungsstellen des Funktionsgraphen mit der x-Achse. Eine Funktion [math]\displaystyle{ f: \mathbb{D} \rightarrow \mathbb{W} }[/math] hat eine Nullstelle bei [math]\displaystyle{ x_0 \in \mathbb{D} }[/math], wenn [math]\displaystyle{ f(x_0)=0 }[/math] gilt.
Beispiele
Lineare Funktion
Nullstellenberechnung für die allgemeine Funktionsvorschrift
Für die lineare Funktion [math]\displaystyle{ f }[/math] mit [math]\displaystyle{ f(x)=mx+b }[/math]
wird die Nullstelle berechnet, indem [math]\displaystyle{ f(x)=0 }[/math] eingesetzt und nach [math]\displaystyle{ x }[/math] umgeformt wird:
[math]\displaystyle{ f(x)=mx+b }[/math]
[math]\displaystyle{ 0=mx+b\ ~|~-b }[/math]
[math]\displaystyle{ -b=\ mx ~|~ : m }[/math]
[math]\displaystyle{ -\frac{b}{m}= x }[/math] ist die Nullstelle.
Nullstellenberechnung für eine konkrete Funktionsvorschrift
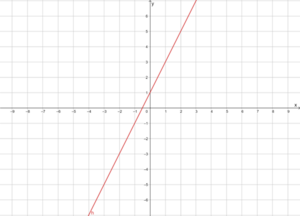
Gegeben ist die lineare Funktion
[math]\displaystyle{ f(x)=2x+1 }[/math]
Setzt man [math]\displaystyle{ f(x)=0 }[/math] ein, folgt
[math]\displaystyle{ 0=2x+1~|~-1 }[/math]
[math]\displaystyle{ -1=\ 2x~|~:2 }[/math]
[math]\displaystyle{ -\frac{1}{2}=\ x }[/math] ist die Nullstelle.
Lineare Funktion ohne Nullstelle
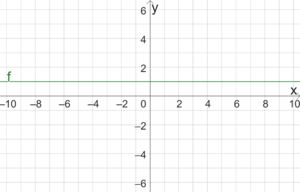
Gegeben ist die lineare Funktion
[math]\displaystyle{ f(x)=0x+1 }[/math]
Die Steigung ist 0 und der y-Achsenabschnitt ist 1. Berechnen wir die Nullstelle, erhalten wir:
[math]\displaystyle{ 0=0x+1 }[/math]
[math]\displaystyle{ 0 = 1 }[/math]
Das ist ein Widerspruch, da [math]\displaystyle{ 0\neq 1 }[/math] ist. Die lineare Funktion hat also keine Nullstelle. Dies erkennt man auch am Graphen der Funktion, da dieser parallel zur [math]\displaystyle{ x }[/math]-Achse verläuft und damit keine Nullstellen hat.
Lineare Funktion mit unendlich vielen Nullstellen
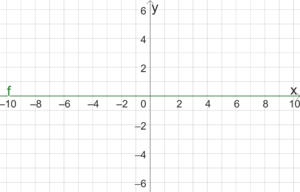
Gegeben ist die lineare Funktion
[math]\displaystyle{ f(x)=0x+0 }[/math]
Die Steigung ist 0 und der y-Achsenabschnitt ist 0. Berechnen wir die Nullstellen, erhalten wir:
[math]\displaystyle{ 0=0x+0 }[/math]
[math]\displaystyle{ 0= 0 }[/math]
Die Aussage ist wahr, also ist jeder [math]\displaystyle{ x }[/math]-Wert eine Nullstelle von [math]\displaystyle{ f }[/math]. Der Graph verläuft vollständig auf der x-Achse.