Extremwert: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „In der Mathematik ist ein Extremwert der Oberbegriff für ein lokales oder globales Maximum oder Minimum. Ein lokales Maximum bzw. lokales Minimum ist der Wert der Funktion an einer Stelle <math>x</math>, wenn in einer Umgebung um <math>x</math> kein größerer oder kleinerer Funktionswert existiert. ==Definition== Es sei <math>I=(a;b)</math> ein Intervall, auf dem die Funktion <math>f</math> Funktion#Definitions-_und_Wer…“ |
|||
| Zeile 81: | Zeile 81: | ||
Damit ist <math>g(0,5)=1,25</math> ein Maximum und <math>H(0,5|1,25)</math> ein Hochpunkt. | Damit ist <math>g(0,5)=1,25</math> ein Maximum und <math>H(0,5|1,25)</math> ein Hochpunkt. | ||
====Graphische Erläuterung der | ====Graphische Erläuterung der Berechnungen==== | ||
<math>x_0=-0,5</math> ist [[Nullstelle]] von <math>f'</math> und Extremstelle von <math>f</math>. <math>f'</math> hat außerdem bei <math>x_0</math> einen Vorzeichenwechsel von negativ zu positiv, das heißt der [[Graph]] zu <math>f</math> fällt vor <math>x_0</math> und steigt anschließend. Damit kann <math>f(x_0)</math> nur ein Minimum sein. Es gilt <math>f''(x_0)=2</math>, damit ist die Steigung von <math>f'</math> in <math>x_0</math> positiv. Da <math>x_0</math> [[Nullstelle]] von <math>f'</math> ist, muss <math>f'</math> bei <math>x_0</math> einen Vorzeichenwechsel von negativ zu positiv haben. | <math>x_0=-0,5</math> ist [[Nullstelle]] von <math>f'</math> und Extremstelle von <math>f</math>. <math>f'</math> hat außerdem bei <math>x_0</math> einen Vorzeichenwechsel von negativ zu positiv, das heißt der [[Graph]] zu <math>f</math> fällt vor <math>x_0</math> und steigt anschließend. Damit kann <math>f(x_0)</math> nur ein Minimum sein. Es gilt <math>f''(x_0)=2</math>, damit ist die Steigung von <math>f'</math> in <math>x_0</math> positiv. Da <math>x_0</math> [[Nullstelle]] von <math>f'</math> ist, muss <math>f'</math> bei <math>x_0</math> einen Vorzeichenwechsel von negativ zu positiv haben. | ||
Version vom 8. Juli 2024, 11:38 Uhr
In der Mathematik ist ein Extremwert der Oberbegriff für ein lokales oder globales Maximum oder Minimum. Ein lokales Maximum bzw. lokales Minimum ist der Wert der Funktion an einer Stelle [math]\displaystyle{ x }[/math], wenn in einer Umgebung um [math]\displaystyle{ x }[/math] kein größerer oder kleinerer Funktionswert existiert.
Definition
Es sei [math]\displaystyle{ I=(a;b) }[/math] ein Intervall, auf dem die Funktion [math]\displaystyle{ f }[/math] definiert ist. Der Funktionswert [math]\displaystyle{ f(x_0) }[/math] heißt lokales Maximum von [math]\displaystyle{ f }[/math], wenn [math]\displaystyle{ f(x)\leq f(x_0) }[/math] für alle [math]\displaystyle{ x \in I }[/math] gilt. Der Funktionswert [math]\displaystyle{ f(x_0) }[/math] heißt lokales Minimum von [math]\displaystyle{ f }[/math], wenn [math]\displaystyle{ f(x)\geq f(x_0) }[/math] für alle [math]\displaystyle{ x \in I }[/math] gilt. [math]\displaystyle{ x_0 }[/math] heißt dann Maximalstelle bzw. Minimalstelle. Der Punkt [math]\displaystyle{ P(x_0| f(x_0)) }[/math] heißt bei einem lokalen Maximum Hochpunkt und bei einem lokalen Minimum Tiefpunkt.
Gilt [math]\displaystyle{ I=\mathbb{D}_f }[/math], dann heißt [math]\displaystyle{ f(x_0) }[/math] auch globales Maximum von [math]\displaystyle{ f }[/math] bzw. globales Minimum von [math]\displaystyle{ f }[/math]. Man nennt Hoch- und Tiefpunkte auch Extrempunkte. [math]\displaystyle{ x_0 }[/math] heißt dann Extremstelle und [math]\displaystyle{ f\left(x_0\right) }[/math] heißt dann Extremwert oder Extremum.
Extremwerte bestimmen
Extremwerte lassen sich mit Hilfe der Ableitungsfunktion bestimmen. Dafür werden die folgenden Bedingungen verwendet und anschließend wird der Extremwert berechnet.
Notwendige Bedingung für Extremstellen
Für eine Funktion [math]\displaystyle{ f }[/math], die an der Stelle [math]\displaystyle{ x_0 \in \mathbb{D}_f }[/math] differenzierbar ist, gilt:
Wenn der Graph der Funktion [math]\displaystyle{ f }[/math] an der Stelle [math]\displaystyle{ x_0 \in \mathbb{D}_f }[/math] einen Extrempunkt besitzt, dann ist [math]\displaystyle{ f'(x_0)=0 }[/math]. D. h. [math]\displaystyle{ x_0 }[/math] ist eine Nullstelle von [math]\displaystyle{ f' }[/math].
Hinreichende Bedingung für Extremstellen
Für eine Funktion [math]\displaystyle{ f }[/math] mit der Ableitungsfunktion [math]\displaystyle{ f' }[/math] in einem Intervall gilt:
Wenn [math]\displaystyle{ f' }[/math] an der Stelle [math]\displaystyle{ x_0 \in \mathbb{D}_f }[/math] eine Nullstelle hat und [math]\displaystyle{ f' }[/math] bei [math]\displaystyle{ x_0 }[/math] die [math]\displaystyle{ x }[/math]-Achse schneidet, dann hat der Graph der Funktion [math]\displaystyle{ f }[/math] an der Stelle [math]\displaystyle{ x_0 }[/math] einen Extrempunkt.
Falls die zweite Ableitung [math]\displaystyle{ f'' }[/math] existiert, so gilt:
Ist [math]\displaystyle{ f'(x_0)=0 }[/math] und [math]\displaystyle{ f''(x_0)\neq0 }[/math], dann hat der Graph der Funktion [math]\displaystyle{ f }[/math] an der Stelle [math]\displaystyle{ x_0 }[/math] einen Extrempunkt. Gilt [math]\displaystyle{ f''(x_0)\gt 0 }[/math] liegt ein Minimum vor. Gilt [math]\displaystyle{ f''(x_0)\lt 0 }[/math] liegt ein Maximum vor.
Extremwert berechnen
Erfüllt ein [math]\displaystyle{ x_0 \in \mathbb{D}_f }[/math] die notwendige und die hinreichende Bedingung, dann ist [math]\displaystyle{ x_0 }[/math] eine Extremstelle. Der Extremwert wird dann durch [math]\displaystyle{ f(x_0) }[/math] berechnet.
Beispiele
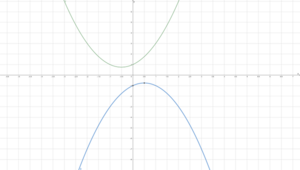
Graphen mit Extrempunkten
Wir betrachten [math]\displaystyle{ f(x)=x^2+x+1 }[/math] und [math]\displaystyle{ g(x)=-x^2+x-1 }[/math] im Intervall [math]\displaystyle{ I=\left(-2;2\right) }[/math]. Der Graph von [math]\displaystyle{ f }[/math] ist grün und der Graph von [math]\displaystyle{ g }[/math] ist blau. [math]\displaystyle{ f }[/math] hat [math]\displaystyle{ T(-0,5|0,75) }[/math] als Tiefpunkt und [math]\displaystyle{ g }[/math] hat [math]\displaystyle{ H(0,5|-0,75) }[/math] Punkt als Hochpunkt. Das lokale Minimum von [math]\displaystyle{ f }[/math] ist [math]\displaystyle{ 0,75 }[/math]. Das lokale Maximum von [math]\displaystyle{ g }[/math] ist [math]\displaystyle{ -0,75 }[/math]. In diesem Fall sind die Extrema auch global.
Extrempunkte rechnerisch ermitteln
Tiefpunkt berechnen
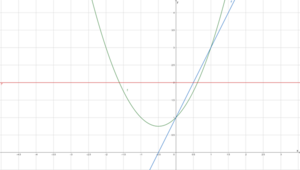
Wir betrachten wieder [math]\displaystyle{ f(x)=x^2+x+1 }[/math] und ändern [math]\displaystyle{ g }[/math] zu [math]\displaystyle{ g\left(x\right)=-x^2+x+1 }[/math]. Für die Ableitungen gilt [math]\displaystyle{ f'(x)=2x+1 }[/math], [math]\displaystyle{ f''(x)=2 }[/math] und [math]\displaystyle{ g'\left(x\right)=-2x+1 }[/math], [math]\displaystyle{ g''\left(x\right)=-2 }[/math].
1. Notwendige Bedingung:
[math]\displaystyle{ 2x+1=0 | -1 }[/math]
[math]\displaystyle{ 2x=-1 | :2 }[/math]
[math]\displaystyle{ x=-0,5 }[/math]
[math]\displaystyle{ x_0=-0,5 }[/math] kommt damit als Extremstelle in Frage.
2. Hinreichende Bedingung:
Da [math]\displaystyle{ f'\left(-1\right)=-1 }[/math] und [math]\displaystyle{ f'\left(0\right)=1 }[/math] gilt, schneidet [math]\displaystyle{ f' }[/math] die [math]\displaystyle{ x }[/math]-Achse bei [math]\displaystyle{ x_0=-0,5 }[/math] und hat dort einen Vorzeichenwechsel von negativ zu positiv.
Alternativ gilt [math]\displaystyle{ f''\left(-0,5\right)=2\gt 0 }[/math]. Also besitzt der Graph von [math]\displaystyle{ f }[/math] einen Tiefpunkt bei [math]\displaystyle{ x_0=-0,5 }[/math].
3. Extremwert berechnen:
Setzen wir [math]\displaystyle{ x_0=-0,5 }[/math] in [math]\displaystyle{ f }[/math] ein, erhalten wir [math]\displaystyle{ f(-0,5)=0,75 }[/math]. Damit ist [math]\displaystyle{ T(-0,5|0,75) }[/math] der Tiefpunkt.
Hochpunkt berechnen
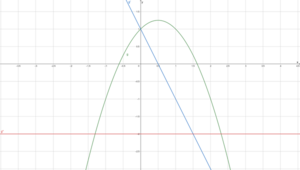
Für [math]\displaystyle{ g }[/math] gehen wir analog vor. Es gilt
1. Notwendige Bedingung:
[math]\displaystyle{ -2x+1=0 | -1 }[/math]
[math]\displaystyle{ -2x=-1 | :(-2) }[/math]
[math]\displaystyle{ x=0,5 }[/math]
2. Hinreichende Bedingung:
Es gilt [math]\displaystyle{ g'(0)=1 }[/math] und [math]\displaystyle{ g'(1)=-1 }[/math]. [math]\displaystyle{ f' }[/math] hat also einen Vorzeichenwechsel von positiv zu negativ.
Alternativ gilt [math]\displaystyle{ g''(0,5)=-2\lt 0 }[/math]. Also besitzt der Graph von [math]\displaystyle{ g }[/math] einen Hochpunkt bei [math]\displaystyle{ x_0=0,5 }[/math].
3. Extremwert berechnen:
Damit ist [math]\displaystyle{ g(0,5)=1,25 }[/math] ein Maximum und [math]\displaystyle{ H(0,5|1,25) }[/math] ein Hochpunkt.
Graphische Erläuterung der Berechnungen
[math]\displaystyle{ x_0=-0,5 }[/math] ist Nullstelle von [math]\displaystyle{ f' }[/math] und Extremstelle von [math]\displaystyle{ f }[/math]. [math]\displaystyle{ f' }[/math] hat außerdem bei [math]\displaystyle{ x_0 }[/math] einen Vorzeichenwechsel von negativ zu positiv, das heißt der Graph zu [math]\displaystyle{ f }[/math] fällt vor [math]\displaystyle{ x_0 }[/math] und steigt anschließend. Damit kann [math]\displaystyle{ f(x_0) }[/math] nur ein Minimum sein. Es gilt [math]\displaystyle{ f''(x_0)=2 }[/math], damit ist die Steigung von [math]\displaystyle{ f' }[/math] in [math]\displaystyle{ x_0 }[/math] positiv. Da [math]\displaystyle{ x_0 }[/math] Nullstelle von [math]\displaystyle{ f' }[/math] ist, muss [math]\displaystyle{ f' }[/math] bei [math]\displaystyle{ x_0 }[/math] einen Vorzeichenwechsel von negativ zu positiv haben.