Ableitungsfunktion

Ableitung und Steigung in einem Punkt

Tangente [math]\displaystyle{ t\left(x\right)=2x-1 }[/math] von [math]\displaystyle{ f\left(x\right)=x^2 }[/math] in [math]\displaystyle{ P(1|1) }[/math]

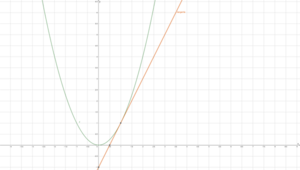
Ist [math]\displaystyle{ f }[/math] eine Funktion, die auf dem Intervall [math]\displaystyle{ [x_0;x_1] \subseteq \mathbb{D}_f }[/math] definiert ist, und strebt der Differenzenquotient [math]\displaystyle{ \frac{f\left(x\right)-f(x_0)}{x-x_0} }[/math] für [math]\displaystyle{ x\rightarrow x_0 }[/math] und [math]\displaystyle{ x \in [x_0;x_1] }[/math] gegen einen Wert, so heißt dieser Wert Ableitung (lokale Änderungsrate) von [math]\displaystyle{ f }[/math] an der Stelle [math]\displaystyle{ x_0 }[/math] und wird mit [math]\displaystyle{ f'(x_0) }[/math] bezeichnet. [math]\displaystyle{ f }[/math] heißt an der Stelle [math]\displaystyle{ x_0 }[/math] differenzierbar.

Die Ableitung ist die Steigung der Tangente im Punkt [math]\displaystyle{ {P(x}_0|f\left(x_0\right)) }[/math] und heißt Steigung des Graphen von [math]\displaystyle{ f }[/math] in [math]\displaystyle{ P }[/math].

Definition

Ist eine Funktion [math]\displaystyle{ f }[/math] für alle [math]\displaystyle{ x\ \in\ \mathbb{D}_f }[/math] differenzierbar, so heißt die Funktion [math]\displaystyle{ f' }[/math], die jeder Stelle [math]\displaystyle{ x }[/math] der Definitionsmenge die Ableitung [math]\displaystyle{ f'(x) }[/math] zuordnet, Ableitungsfunktion. Wir bezeichnen [math]\displaystyle{ f' }[/math] auch als Ableitung von [math]\displaystyle{ f }[/math].

Ableitungsregeln

Die Ableitungsfunktion [math]\displaystyle{ f' }[/math] wird mit den folgenden Regeln ermittelt:

Potenzregel

Die Funktion [math]\displaystyle{ f\left(x\right)=x^n }[/math] hat die Ableitungsfunktion [math]\displaystyle{ f'\left(x\right)=n{\cdot x}^{n-1} }[/math] für [math]\displaystyle{ n\ \in\mathbb{N} }[/math].

Faktorregel

Für [math]\displaystyle{ f\left(x\right)=c\cdot g(x) }[/math] gilt [math]\displaystyle{ f'\left(x\right)=c\cdot g'(x) }[/math].

Summenregel

Für [math]\displaystyle{ f\left(x\right)=g\left(x\right)+h(x) }[/math] gilt [math]\displaystyle{ f'\left(x\right)=g'\left(x\right)+h'(x) }[/math].

Beispiele

Graphische Erläuterung der Steigung in einem Punkt

Graph der Funktion [math]\displaystyle{ f(x)=sin(2x) }[/math]

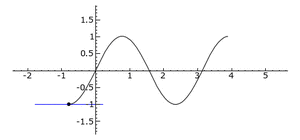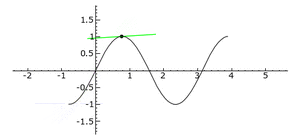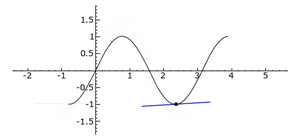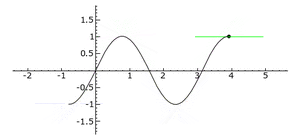
Im Bild wandert ein Punkt mit seiner Tangente über den Graph der Funktion [math]\displaystyle{ f }[/math]. Die Steigung der Tangente ist die Steigung in dem Punkt. Wandert der Punkt den 'Berg' hinauf, ist die Steigung positiv. Wandert der Punkt den 'Berg' hinab, ist die Steigung negativ. Auf dem 'Berg' und im 'Tal' ist die Steigung Null. In der Mitte zwischen 'Berg' und 'Tal' ist die Steigung betragsmäßig am größten.

Steigung in einem Punkt mit Hilfe der Tangente ermitteln

Wir betrachten [math]\displaystyle{ f\left(x\right)=x^2 }[/math] im Punkt [math]\displaystyle{ P(1|1) }[/math]. Die Tangente in diesem Punkt ist [math]\displaystyle{ t\left(x\right)=2x-1 }[/math]. Die Steigung von [math]\displaystyle{ f }[/math] in [math]\displaystyle{ P }[/math] ist [math]\displaystyle{ 2 }[/math].

Regeln anwenden anwenden

Potenzregel

• Für [math]\displaystyle{ f(x)=x^6 }[/math] gilt [math]\displaystyle{ f'(x)=6x^{6-1}=6x^5 }[/math]. Die Steigung im Punkt [math]\displaystyle{ P(1|2) }[/math] ist dann [math]\displaystyle{ f'(1)=6 \cdot 1^5=6 }[/math].
• Für [math]\displaystyle{ f(x)=x }[/math] gilt [math]\displaystyle{ f'(x)=1 }[/math].
• Für [math]\displaystyle{ f(x)=-5 }[/math] gilt [math]\displaystyle{ f'(x)=0 }[/math].
• Für [math]\displaystyle{ f(x)=x^{-3} }[/math] gilt [math]\displaystyle{ g'(x)=-3x^{-3-1}=-3x^{-4} }[/math].

Faktorregel

• Für [math]\displaystyle{ g(x)=3x^5 }[/math] gilt [math]\displaystyle{ g'(x)=3\cdot5x^{5-1}=15x^4 }[/math].
• Für [math]\displaystyle{ f(x)=5x }[/math] gilt [math]\displaystyle{ f'(x)=5 }[/math].
• Für [math]\displaystyle{ g(x)=-3x^{-2} }[/math] gilt [math]\displaystyle{ g'(x)=-3\cdot(-2)\cdot x^{-2-1}=6x^{-3} }[/math].

Summenregel

• Für [math]\displaystyle{ h(x)=2x^3+3x^4 }[/math] gilt [math]\displaystyle{ h'(x)=2\cdot3x^2+4\cdot3x^3 =6x^2+12x^3 }[/math].
• Für [math]\displaystyle{ h(x)=2x-5 }[/math] gilt [math]\displaystyle{ h'(x)=2 }[/math].

Höhere Ableitungen ermitteln

Höhere Ableitungen werden durch mehrmaliges Anwenden der Ableitungsregeln angewendet. Die Ableitungsfunktion von [math]\displaystyle{ f'(x) }[/math] ist dann [math]\displaystyle{ f''(x) }[/math] und die Ableitungsfunktion von [math]\displaystyle{ f''(x) }[/math] ist [math]\displaystyle{ f'''(x) }[/math]. [math]\displaystyle{ f''(x) }[/math] bzw. [math]\displaystyle{ f'''(x) }[/math] bezeichnen wir mit zweite bzw. dritte Ableitung.

Punkt zur Steigung ermitteln

Wir betrachten die Funktion [math]\displaystyle{ f(x)=2x^2 }[/math] und ermitteln den Punkt, in dem der Graph von [math]\displaystyle{ f }[/math] die Steigung [math]\displaystyle{ m=4 }[/math] hat:

1. Es gilt [math]\displaystyle{ f'(x)=4x }[/math].
2. [math]\displaystyle{ 4=4x }[/math]
   [math]\displaystyle{ 1=x }[/math]
3. [math]\displaystyle{ f(1)=2\cdot 1^2=2 }[/math]
   Der Graph von [math]\displaystyle{ f }[/math] hat im Punkt [math]\displaystyle{ P(1|2) }[/math] die Steigung [math]\displaystyle{ m=4 }[/math].