Baumdiagramm

Ein Baum ist ein spezieller Typ von Graph. Im Kontext der Informatik, Mathematik und Datenanalyse ist der Begriff "Baum" eine fundamental wichtige Datenstruktur, die hierarchische Beziehungen darstellt. Er kommt in vielen Bereichen zur Anwendung. Ein Baumdiagramm ist eine visuelle Darstellungsform, die verwendet wird, um Entscheidungen, Möglichkeiten oder Abläufe zu veranschaulichen. Es besteht aus Knoten, die Ereignisse oder Entscheidungen repräsentieren, und Ästen, die die möglichen Ergebnisse oder Schritte verbinden.

Eigenschaften eines Baumdiagramms:

• Knoten: Stellen Entscheidungen oder Ereignisse dar.
• Äste: Zeigen die möglichen Ergebnisse oder Folgeentscheidungen an.
• Hierarchische Struktur: Die Darstellung ist oft hierarchisch, wobei der Ausgangspunkt oben steht und die möglichen Ergebnisse nach unten verzweigen.

Anwendung:

Baumdiagramme finden in verschiedenen Bereichen Anwendung, wie zum Beispiel in der Mathematik zur Darstellung von Wahrscheinlichkeiten, in der Informatik zur Veranschaulichung von Algorithmen oder Entscheidungsprozessen und in der Statistik zur Analyse von Zufallsexperimenten.

Wahrscheinlichkeitsrechnung: Ereignisbäume

In der Wahrscheinlichkeitsrechnung werden Bäume oft als Ereignisbäume oder Wahrscheinlichkeitsbäume verwendet, um eine Sequenz von Ereignissen und deren mögliche Ausgänge sowie die zugehörigen Wahrscheinlichkeiten zu visualisieren und zu berechnen.

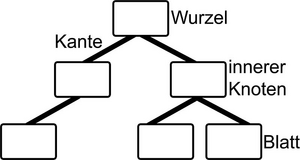
Struktur

• Knoten: Repräsentieren Ereignisse oder Entscheidungspunkte.
• Äste/Kanten: Repräsentieren die möglichen Ausgänge eines Ereignisses oder die getroffenen Entscheidungen, denen Wahrscheinlichkeiten zugeordnet sind.
• Blätter (Endknoten): Repräsentieren die Endergebnisse oder finalen Zustände.

Anwendungsbeispiel

• Medizinische Diagnostik: Ein Arzt kann einen Ereignisbaum verwenden, um die Wahrscheinlichkeit verschiedener Diagnosen basierend auf Symptomen und Testergebnissen zu bestimmen.
  • Startknoten: Patient hat Symptom X.
  • Äste: Test A ist positiv (Wahrscheinlichkeit P(Pos|X)) oder negativ (Wahrscheinlichkeit P(Neg|X)).
  • Nächste Knoten: Basierend auf Testergebnis, weitere Tests oder Diagnosen.
  • Blätter: Wahrscheinlichkeiten für Krankheiten A, B, C.
• Glücksspiele: Berechnung der Wahrscheinlichkeiten für verschiedene Ausgänge bei mehreren Würfen einer Münze oder eines Würfels.
• Risikobewertung: Analyse von Pfaden und Wahrscheinlichkeiten, die zu einem bestimmten Risikoereignis führen können.

Maschinelles Lernen

Im Maschinellen Lernen sind Bäume eine der grundlegendsten und leistungsstärksten Modelltypen, sowohl für Klassifikations- als auch für Regressionsprobleme.

Entscheidungsbäume (als Modell)

• Struktur: Hierarchische Struktur, bei der interne Knoten "Tests" auf Merkmale der Daten repräsentieren (z.B. "Ist Alter > 30?"). Jeder Ast repräsentiert das Ergebnis dieses Tests, und jeder Blattknoten repräsentiert eine Klassenzuordnung (bei Klassifikation) oder einen Wert (bei Regression).
• Lernen: Der Baum wird durch rekursive Partitionierung der Daten gelernt, indem an jedem Knoten das Merkmal ausgewählt wird, das die Daten am besten trennt (z.B. basierend auf Entropie).

Anwendungsbeispiel

• Kreditwürdigkeit: Entscheidung, ob einem Kunden ein Kredit gewährt werden soll, basierend auf Einkommen, Alter, Kredit-Historie etc. Ein Blatt könnte "Kredit gewähren" oder "Kredit ablehnen" sein.
• Krankheitsdiagnose: Klassifikation von Patienten in "krank" oder "gesund" basierend auf Symptomen.

Suche: Suchbäume und Baumtraversierung

Im Bereich der Suche und Datenstrukturen sind Bäume fundamental, um Daten effizient zu speichern und zu durchsuchen.

Suchbäume (z.B. Binäre Suchbäume, B-Bäume, AVL-Bäume, Rot-Schwarz-Bäume)

• Struktur: Jeder Knoten enthält einen Schlüssel (Wert), und die Anordnung der Kinderknoten folgt einer bestimmten Ordnungsregel (z.B. im Binären Suchbaum ist der linke Kindknoten kleiner als der Elternknoten, der rechte größer).

Anwendungsbeispiel

• Datenbanksysteme: Indizierung von Daten für schnellen Zugriff. B-Bäume werden häufig in Datenbanken und Dateisystemen verwendet, um Daten auf Festplatten zu organisieren und zu durchsuchen.
• Wörterbücher/Lexika: Schnelles Auffinden von Wörtern.
• Implementierung von Sets und Maps: Effizientes Speichern und Abrufen von Elementen.

Baumtraversierung (Durchlaufen von Bäumen)

• Algorithmen wie Tiefensuche (Depth-First Search, DFS) und Breitensuche (Breadth-First Search, BFS) werden verwendet, um alle Knoten eines Baumes systematisch zu besuchen.

Anwendungsbeispiel

• Dateisysteme: Das Durchsuchen von Ordnern und Unterordnern auf einer Festplatte (was eine Baumstruktur hat).
• Web-Crawler: Durchlaufen von Links auf Webseiten, um Inhalte zu indexieren (das Web kann als Graph mit Baum-ähnlichen Strukturen betrachtet werden).
• Künstliche Intelligenz (AI): In Spielen wie Schach oder Go werden Spielzustände oft als Bäume modelliert. Suchalgorithmen wie Minimax oder Alpha-Beta-Pruning werden verwendet, um den besten Zug zu finden, indem der Spielbaum durchsucht wird.
• Compilerbau: Die Syntax eines Programmcodes wird oft als Abstrakter Syntaxbaum (AST) dargestellt, der dann durchlaufen wird, um den Code zu analysieren und zu optimieren.