Quadratische Funktion: Unterschied zwischen den Versionen
| (28 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Quadratische Funktionen sind ein wesentlicher Bestandteil der Analysis und damit ein Gebiet der Mathematik. Sie haben viele praktische Anwendungen in verschiedenen Bereichen wie Wirtschaft, Ingenieurwesen, Naturwissenschaften und Sozialwissenschaften und beschreiben die Beziehung zwischen zwei Variablen, die quadratisch miteinander verbunden sind, und können verwendet werden, um Trends, Muster und Veränderungen im Verhalten von Phänomenen zu analysieren und vorherzusagen. | |||
== | ==Definition== | ||
Eine Funktion der Form <math>f\left(x\right)=ax^2+bx+c</math> mit <math>a,~b,~c \in \mathbb{R},~a \neq 0</math> heißt '''quadratische Funktion''' in '''Normalform''', ihr [[Graph]] heißt '''Parabel'''. <math>a</math> heißt '''Streckungsfaktor''', wenn für den [[Betragsfunktion|Betrag]] <math>|a|>1</math> gilt und '''Stauchungsfaktor''', wenn für den [[Betragsfunktion|Betrag]] <math>|a|<1</math> gilt. <math>c</math> ist der '''y-Achsenabschnitt'''. | |||
Für <math>a>0</math> ist die Parabel nach '''oben geöffnet''', für <math>a<0</math> ist die Parabel nach '''unten geöffnet'''. Der tiefste bzw. höchster Punkt heißt '''Scheitelpunkt''' oder '''Scheitel S'''. Der Graph von <math>f(x)=x^2</math> heißt '''Normalparabel'''. | |||
==Nullstellenform== | |||
== | Eine Funktion der Form <math>f(x)=a(x-x_1)(x-x_2)</math> heißt quadratische Funktion in '''Nullstellenform'''. Die [[Nullstelle|Nullstellen]] sind <math>x_1</math> und <math>x_2</math>. | ||
== | ==Scheitelpunktform== | ||
Eine Funktion der Form <math>f | Eine Funktion der Form <math>f(x)=a(x-e)^2+f</math> mit <math>a\neq0</math> heißt quadratische Funktion in '''Scheitelpunktform'''. Der Scheitelpunkt ist <math>S(e|f)</math>. Der Faktor <math>a</math> ist in der Scheitelpunktform und der Normalform der Gleiche. | ||
==Schnittpunkte von Parabeln und Geraden berechnen== | |||
Sind eine lineare Funktion <math>y=mx+b</math> und eine quadratische Funktion <math>y=ax^2+bx+c</math> gegeben, kann die Schnittstelle durch Gleichsetzen, <math>ax^2+bx+c=mx+b\ </math>, und Umformen nach x errechnet werden. Wurde so umgeformt, dass auf einer Seite eine 0 steht, kann die p-q-Formel angewendet werden und wir erhalten die Schnittstellen. Anschließend werden die dazugehörigen y-Werte durch Einsetzen der x-Werte in die quadratische oder lineare Funktion berechnet. Für zwei quadratische Funktionen oder lineare Funktionen ist das Vorgehen analog. | |||
=== | ==Beispiele== | ||
===Begriffe für eine quadratische Funktionsvorschrift verwenden=== | |||
[[Datei:QuadratischeFunktionenBeispielQuadFkt.png|mini|Graph der Funktion <math>E(x)=-0,8x^2+4x</math>]] | [[Datei:QuadratischeFunktionenBeispielQuadFkt.png|mini|Graph der Funktion <math>E(x)=-0,8x^2+4x</math>]] | ||
Der Graph der Funktion <math>E(x)=-0,8x^2+4x</math> mit dem Definitionsbereich <math>\mathbb{D}_E=[0;5]</math> ist auf der rechten Seite dargestellt. Der Scheitelpunkt ist <math>S(2,5|5)</math>. Die Normalparabel wurde um den Faktor <math>-0,8</math> gestaucht und ist nach unten geöffnet. Der Schnittpunkt mit der y-Achse ist <math>(0|0)</math>. | Der Graph der Funktion <math>E(x)=-0,8x^2+4x</math> mit dem Definitionsbereich <math>\mathbb{D}_E=[0;5]</math> ist auf der rechten Seite dargestellt. Der Scheitelpunkt ist <math>S(2,5|5)</math>. Die Normalparabel wurde um den Faktor <math>-0,8</math> gestaucht und ist nach unten geöffnet. Der Schnittpunkt mit der y-Achse ist <math>(0|0)</math>. | ||
[[Datei:QuadratischeFunktionenBeispielQuadFktNormal.png|mini|Graph der Funktion <math>f(x)=x^2</math>]] | [[Datei:QuadratischeFunktionenBeispielQuadFktNormal.png|mini|Graph der Funktion <math>f(x)=x^2</math>]] | ||
Der nächste Graph ist die Normalparabel zur Funktion <math>f(x)=x^2</math> mit dem Scheitelpunkt <math>S(0|0)</math> und wurde daher weder gestaucht, noch gestreckt, da <math>a=1</math> ist. Der Schnittpunkt mit der y-Achse ist <math>(0 | Der nächste Graph ist die Normalparabel zur Funktion <math>f(x)=x^2</math> mit dem Scheitelpunkt <math>S(0|0)</math> und wurde daher weder gestaucht, noch gestreckt, da <math>a=1</math> ist. Der Schnittpunkt mit der y-Achse ist <math>(0|0)</math>. | ||
[[Datei:QuadratischeFunktionenBeispielQuadFktGestreckt.png|mini|Graph der Funktion <math>f(x)=5x^2</math>]] | [[Datei:QuadratischeFunktionenBeispielQuadFktGestreckt.png|mini|Graph der Funktion <math>f(x)=5x^2</math>]] | ||
Der letzte Graph | Der letzte Graph hat die Funktionsvorschrift <math>f(x)=5x^2</math> mit dem Scheitelpunkt <math>S(0|0)</math> und wurde gestreckt, da <math>a=5</math> ist. Der Schnittpunkt mit der y-Achse ist <math>(0/0)</math>. | ||
<html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/64UjI-hUQIU?si=2PmAymgjsY8d9YsQ" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe><iframe width="280" height="157.5" src="https://www.youtube.com/embed/_1k7_zaN4q4?si=tNfzoDlVV4Q2tRmx" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | <html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/64UjI-hUQIU?si=2PmAymgjsY8d9YsQ" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe><iframe width="280" height="157.5" src="https://www.youtube.com/embed/_1k7_zaN4q4?si=tNfzoDlVV4Q2tRmx" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | ||
== | ===Nullstellenform mit positiver und negativer [[Nullstelle]]=== | ||
<math>x_1=3</math> und <math>x_2=-4</math> sind [[Nullstelle|Nullstellen]] von <math>f</math> mit <math>a=1</math>, dann ist <math>f\left(x\right)=1 \cdot (x-3)\cdot (x+4)</math> die Nullstellenform von <math>f</math>. | |||
=== | ===Nullstellenform mit positiven [[Nullstelle|Nullstellen]]=== | ||
[[Datei: | <math>x_1=2</math> und <math>x_2=6</math> sind [[Nullstelle|Nullstellen]] von <math>g</math> mit <math>a=-3</math>, dann ist <math>g\left(x\right)=(-3)\cdot (x-2) \cdot (x-6)</math> die Nullstellenform von <math>g</math>. | ||
Wir betrachten <math> | |||
<html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/u0oN0VTA9Uo?si=bBxM4O5loope1XEI" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | |||
===Scheitelpunktsform in Normalform überführen=== | |||
[[Datei:QuadratischeFunktionenBeispielQuadFktScheitelpf.png|mini|Graph der Funktion <math>f(x)=-2(x-2)^2+1</math>]] | |||
Wir betrachten die Funktion <math>f\left(x\right)=-2(x-2)^2+1</math>. Der Scheitelpunkt ist dann <math>S(2|1)</math>. Man kann die rechte Seite der Funktionsvorschrift weiter auflösen, um von der Scheitelpunktform zur Normalform zu kommen: | |||
<math>f\left(x\right)=-2({x-2)}^2+1</math> | |||
<math> | <math>f\left(x\right)=-2(x^2-4x+4)+1</math> | ||
<math>x^2+ | <math>f\left(x\right)=-2x^2+8x-8+1</math> | ||
<math>f\left(x\right)=-2x^2+8x-7</math> | |||
Der Schnittpunkt mit der y-Achse ist <math>(0|-7)</math>. | |||
===Schnittpunkte von Parabeln berechnen=== | |||
Wir betrachten im Folgenden die drei Fälle für Schnittpunkte von Parabel und Gerade sowie den Fall, dass zwei Parabeln sich nicht schneiden. | |||
=== | ====Parabel und Gerade haben keinen Schnittpunkt==== | ||
[[Datei:QuadratischeFunktionenBeispielKeinSchnitt.png|mini|Graphen der Funktionen <math>{f\left(x\right)=2x}^2+4x+4</math> und <math>g\left(x\right)=-2x-1</math> ohne Schnittpunkt]] | |||
Wir betrachten <math>{f\left(x\right)=2x}^2+4x+4</math> und <math>g\left(x\right)=-2x-1</math>. Wir setzen die Funktionen gleich und rechnen | |||
<math>{2x}^2+4x+4=-2x-1~|~+1</math> | |||
<math> | <math>{2x}^2+4x+5=-2x~|~+2x</math> | ||
<math> | <math>{2x}^2+6x+5=0~|~:2</math> | ||
<math>x | <math>x^2+3x+2,5=0</math> | ||
<math>x= | damit wir die p-q-Formel anwenden können. Es gilt p=3 und q=2,5. Diese Werte können wir in die p-q-Formel einsetzen: | ||
<math>x=-\frac{3}{2}\pm\sqrt{\left(\frac{3}{2}\right)^2-2,5}=-1,5\pm\sqrt{-0,25}</math> | |||
Aus negativen Zahlen können wir keine Wurzel ziehen, daher existiert keine Schnittstelle. Das lässt sich auch im Koordinatensystem erkennen. | |||
<math>\left(x- | ====Parabel und Gerade haben genau einen Schnittpunkt==== | ||
[[Datei:QuadratischeFunktionenBeispielEinSchnitt.png|mini|Graphen der Funktionen <math>{f\left(x\right)=2x}^2+4x+4</math> und <math>g\left(x\right)=-2x-0,5</math> mit genau einem Schnittpunkt]] | |||
Wir betrachten <math>{f\left(x\right)=2x}^2+4x+4</math> und <math>g\left(x\right)=-2x-0,5</math>. Wir setzen die Funktionen gleich und rechnen | |||
<math> | <math>{2x}^2+4x+4=-2x-0,5~|~+0,5</math> | ||
<math> | <math>{2x}^2+4x+4,5=-2x~|~+2x</math> | ||
<math>{2x}^2+6x+4,5=0~|~:2</math> | |||
<math> | |||
<math>x^2 | <math>x^2+3x+2,25=0</math> | ||
<math>x | damit wir die p-q-Formel anwenden können. Es gilt <math>p=3</math> und <math>q=2,25</math>. Diese Werte können wir in die p-q-Formel einsetzen: | ||
<math>x=-\frac{3}{2}\pm\sqrt{\left(\frac{3}{2}\right)^2-2,25}=-1,5\pm\sqrt0=-1,5</math> | |||
<math> | Den y-Wert berechnen wir durch <math>g\left(-1,5\right)=-2\cdot\left(-1,5\right)-0,5=2,5</math>. Der Schnittpunkt ist damit <math>A(-1,5|2,5)</math>. | ||
=== | ====Parabel und Gerade haben zwei Schnittpunkte==== | ||
[[Datei:QuadratischeFunktionenBeispielZweiSchnitt.png|mini|Graphen der Funktionen <math>{f\left(x\right)=2x}^2+4x+4</math> und <math>g\left(x\right)=-2x</math> mit zwei Schnittpunkten]] | |||
Wir betrachten <math>{f\left(x\right)=2x}^2+4x+4</math> und <math>g\left(x\right)=-2x</math>. Wir setzen die Funktionen gleich und rechnen | |||
<math> | <math>{2x}^2+4x+4=-2x\ |+2x</math> | ||
<math> | <math>{2x}^2+6x+4=0~|~:2</math> | ||
<math> | <math>x^2+3x+2=0</math> | ||
<math> | damit wir die p-q-Formel anwenden können. Es gilt <math>p=3</math> und <math>q=2</math>. Diese Werte können wir in die p-q-Formel einsetzen: | ||
<math> | <math>x_1=-\frac{3}{2}+\sqrt{\left(\frac{3}{2}\right)^2-2}=-1,5+\sqrt{0,25}=-1</math> | ||
und | |||
<math>x_2=-\frac{3}{2}-\sqrt{\left(\frac{3}{2}\right)^2-2}=-1,5-\sqrt{0,25}=-2</math> | |||
<math> | Die y-Werte berechnen wir durch <math>g\left(-1\right)=-2\cdot\left(-1\right)=2</math> und <math>g\left(-2\right)=-2\cdot\left(-2\right)=4</math>. Die Schnittpunkte sind damit <math>A(-1|2)</math> und <math>B(-2|4)</math>. | ||
====Zwei Parabeln ohne Schnittpunkt==== | |||
[[Datei:QuadratischeFunktionenBeispielParaOhneSchnitt.png|mini|Graphen der Funktionen <math>{f\left(x\right)=2x}^2+4x+4</math> und <math>{h\left(x\right)=-3x}^2-2x+1</math> ohne Schnittpunkt]] | |||
Betrachten wir zwei Parabeln, treten die gleichen drei Fälle wie oben auf. Wir betrachten hier nur den Fall, bei dem die Parabeln keine Schnittpunkte haben. | |||
Wir betrachten <math>{f\left(x\right)=2x}^2+4x+4</math> und <math>{h\left(x\right)=-3x}^2-2x+1</math>. Gleichsetzen der Funktionen liefert | |||
<math>h(x)=f(x)</math> | |||
<math>-3x^2-2x+1=2x^2+4x+4~|~-2x^2</math> | |||
<math>{-5x}^2-2x+1=4x+4~|~-4x</math> | |||
<math>{-5x}^2-6x+1=4~|~-4</math> | |||
<math> | <math>{-5x}^2-6x-3=0~|~:(-5)</math> | ||
<math> | <math>x^2+1,2x+0,6=0</math> | ||
<math> | Es gilt <math>p=1,2</math> und <math>q=0,6</math>. | ||
Diese Werte können wir einsetzen: | |||
<math>x=-\frac{1,2}{2}\pm\sqrt{\left(\frac{1,2}{2}\right)^2-0,6}=-0,6\pm\sqrt{-0,24}</math> | |||
Der Wert unter der Wurzel ist negativ und damit existiert kein Schnittpunkt. | |||
<html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/FAqb0Ld_4Do?si=NaHcBx5HFGIFgCcf" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | |||
[[Kategorie:Mathematische Funktion]] | |||
[[Kategorie:FHR_WuV_Mathe]] | |||
Aktuelle Version vom 9. April 2025, 13:05 Uhr
Quadratische Funktionen sind ein wesentlicher Bestandteil der Analysis und damit ein Gebiet der Mathematik. Sie haben viele praktische Anwendungen in verschiedenen Bereichen wie Wirtschaft, Ingenieurwesen, Naturwissenschaften und Sozialwissenschaften und beschreiben die Beziehung zwischen zwei Variablen, die quadratisch miteinander verbunden sind, und können verwendet werden, um Trends, Muster und Veränderungen im Verhalten von Phänomenen zu analysieren und vorherzusagen.
Definition
Eine Funktion der Form [math]\displaystyle{ f\left(x\right)=ax^2+bx+c }[/math] mit [math]\displaystyle{ a,~b,~c \in \mathbb{R},~a \neq 0 }[/math] heißt quadratische Funktion in Normalform, ihr Graph heißt Parabel. [math]\displaystyle{ a }[/math] heißt Streckungsfaktor, wenn für den Betrag [math]\displaystyle{ |a|\gt 1 }[/math] gilt und Stauchungsfaktor, wenn für den Betrag [math]\displaystyle{ |a|\lt 1 }[/math] gilt. [math]\displaystyle{ c }[/math] ist der y-Achsenabschnitt.
Für [math]\displaystyle{ a\gt 0 }[/math] ist die Parabel nach oben geöffnet, für [math]\displaystyle{ a\lt 0 }[/math] ist die Parabel nach unten geöffnet. Der tiefste bzw. höchster Punkt heißt Scheitelpunkt oder Scheitel S. Der Graph von [math]\displaystyle{ f(x)=x^2 }[/math] heißt Normalparabel.
Nullstellenform
Eine Funktion der Form [math]\displaystyle{ f(x)=a(x-x_1)(x-x_2) }[/math] heißt quadratische Funktion in Nullstellenform. Die Nullstellen sind [math]\displaystyle{ x_1 }[/math] und [math]\displaystyle{ x_2 }[/math].
Scheitelpunktform
Eine Funktion der Form [math]\displaystyle{ f(x)=a(x-e)^2+f }[/math] mit [math]\displaystyle{ a\neq0 }[/math] heißt quadratische Funktion in Scheitelpunktform. Der Scheitelpunkt ist [math]\displaystyle{ S(e|f) }[/math]. Der Faktor [math]\displaystyle{ a }[/math] ist in der Scheitelpunktform und der Normalform der Gleiche.
Schnittpunkte von Parabeln und Geraden berechnen
Sind eine lineare Funktion [math]\displaystyle{ y=mx+b }[/math] und eine quadratische Funktion [math]\displaystyle{ y=ax^2+bx+c }[/math] gegeben, kann die Schnittstelle durch Gleichsetzen, [math]\displaystyle{ ax^2+bx+c=mx+b\ }[/math], und Umformen nach x errechnet werden. Wurde so umgeformt, dass auf einer Seite eine 0 steht, kann die p-q-Formel angewendet werden und wir erhalten die Schnittstellen. Anschließend werden die dazugehörigen y-Werte durch Einsetzen der x-Werte in die quadratische oder lineare Funktion berechnet. Für zwei quadratische Funktionen oder lineare Funktionen ist das Vorgehen analog.
Beispiele
Begriffe für eine quadratische Funktionsvorschrift verwenden
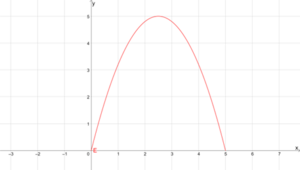
Der Graph der Funktion [math]\displaystyle{ E(x)=-0,8x^2+4x }[/math] mit dem Definitionsbereich [math]\displaystyle{ \mathbb{D}_E=[0;5] }[/math] ist auf der rechten Seite dargestellt. Der Scheitelpunkt ist [math]\displaystyle{ S(2,5|5) }[/math]. Die Normalparabel wurde um den Faktor [math]\displaystyle{ -0,8 }[/math] gestaucht und ist nach unten geöffnet. Der Schnittpunkt mit der y-Achse ist [math]\displaystyle{ (0|0) }[/math].
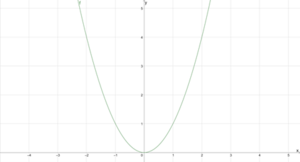
Der nächste Graph ist die Normalparabel zur Funktion [math]\displaystyle{ f(x)=x^2 }[/math] mit dem Scheitelpunkt [math]\displaystyle{ S(0|0) }[/math] und wurde daher weder gestaucht, noch gestreckt, da [math]\displaystyle{ a=1 }[/math] ist. Der Schnittpunkt mit der y-Achse ist [math]\displaystyle{ (0|0) }[/math].
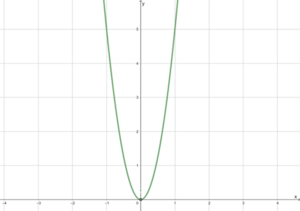
Der letzte Graph hat die Funktionsvorschrift [math]\displaystyle{ f(x)=5x^2 }[/math] mit dem Scheitelpunkt [math]\displaystyle{ S(0|0) }[/math] und wurde gestreckt, da [math]\displaystyle{ a=5 }[/math] ist. Der Schnittpunkt mit der y-Achse ist [math]\displaystyle{ (0/0) }[/math].
Nullstellenform mit positiver und negativer Nullstelle
[math]\displaystyle{ x_1=3 }[/math] und [math]\displaystyle{ x_2=-4 }[/math] sind Nullstellen von [math]\displaystyle{ f }[/math] mit [math]\displaystyle{ a=1 }[/math], dann ist [math]\displaystyle{ f\left(x\right)=1 \cdot (x-3)\cdot (x+4) }[/math] die Nullstellenform von [math]\displaystyle{ f }[/math].
Nullstellenform mit positiven Nullstellen
[math]\displaystyle{ x_1=2 }[/math] und [math]\displaystyle{ x_2=6 }[/math] sind Nullstellen von [math]\displaystyle{ g }[/math] mit [math]\displaystyle{ a=-3 }[/math], dann ist [math]\displaystyle{ g\left(x\right)=(-3)\cdot (x-2) \cdot (x-6) }[/math] die Nullstellenform von [math]\displaystyle{ g }[/math].
Scheitelpunktsform in Normalform überführen
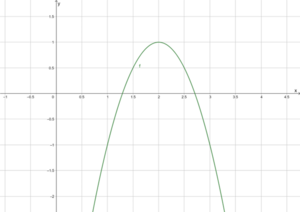
Wir betrachten die Funktion [math]\displaystyle{ f\left(x\right)=-2(x-2)^2+1 }[/math]. Der Scheitelpunkt ist dann [math]\displaystyle{ S(2|1) }[/math]. Man kann die rechte Seite der Funktionsvorschrift weiter auflösen, um von der Scheitelpunktform zur Normalform zu kommen:
[math]\displaystyle{ f\left(x\right)=-2({x-2)}^2+1 }[/math]
[math]\displaystyle{ f\left(x\right)=-2(x^2-4x+4)+1 }[/math]
[math]\displaystyle{ f\left(x\right)=-2x^2+8x-8+1 }[/math]
[math]\displaystyle{ f\left(x\right)=-2x^2+8x-7 }[/math]
Der Schnittpunkt mit der y-Achse ist [math]\displaystyle{ (0|-7) }[/math].
Schnittpunkte von Parabeln berechnen
Wir betrachten im Folgenden die drei Fälle für Schnittpunkte von Parabel und Gerade sowie den Fall, dass zwei Parabeln sich nicht schneiden.
Parabel und Gerade haben keinen Schnittpunkt
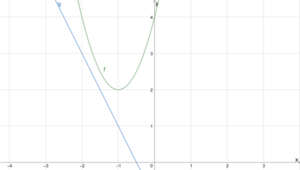
Wir betrachten [math]\displaystyle{ {f\left(x\right)=2x}^2+4x+4 }[/math] und [math]\displaystyle{ g\left(x\right)=-2x-1 }[/math]. Wir setzen die Funktionen gleich und rechnen
[math]\displaystyle{ {2x}^2+4x+4=-2x-1~|~+1 }[/math]
[math]\displaystyle{ {2x}^2+4x+5=-2x~|~+2x }[/math]
[math]\displaystyle{ {2x}^2+6x+5=0~|~:2 }[/math]
[math]\displaystyle{ x^2+3x+2,5=0 }[/math]
damit wir die p-q-Formel anwenden können. Es gilt p=3 und q=2,5. Diese Werte können wir in die p-q-Formel einsetzen: [math]\displaystyle{ x=-\frac{3}{2}\pm\sqrt{\left(\frac{3}{2}\right)^2-2,5}=-1,5\pm\sqrt{-0,25} }[/math]
Aus negativen Zahlen können wir keine Wurzel ziehen, daher existiert keine Schnittstelle. Das lässt sich auch im Koordinatensystem erkennen.
Parabel und Gerade haben genau einen Schnittpunkt
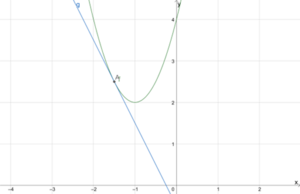
Wir betrachten [math]\displaystyle{ {f\left(x\right)=2x}^2+4x+4 }[/math] und [math]\displaystyle{ g\left(x\right)=-2x-0,5 }[/math]. Wir setzen die Funktionen gleich und rechnen
[math]\displaystyle{ {2x}^2+4x+4=-2x-0,5~|~+0,5 }[/math]
[math]\displaystyle{ {2x}^2+4x+4,5=-2x~|~+2x }[/math]
[math]\displaystyle{ {2x}^2+6x+4,5=0~|~:2 }[/math]
[math]\displaystyle{ x^2+3x+2,25=0 }[/math]
damit wir die p-q-Formel anwenden können. Es gilt [math]\displaystyle{ p=3 }[/math] und [math]\displaystyle{ q=2,25 }[/math]. Diese Werte können wir in die p-q-Formel einsetzen: [math]\displaystyle{ x=-\frac{3}{2}\pm\sqrt{\left(\frac{3}{2}\right)^2-2,25}=-1,5\pm\sqrt0=-1,5 }[/math]
Den y-Wert berechnen wir durch [math]\displaystyle{ g\left(-1,5\right)=-2\cdot\left(-1,5\right)-0,5=2,5 }[/math]. Der Schnittpunkt ist damit [math]\displaystyle{ A(-1,5|2,5) }[/math].
Parabel und Gerade haben zwei Schnittpunkte
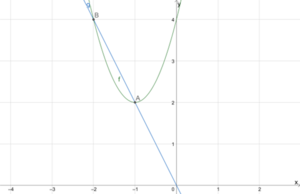
Wir betrachten [math]\displaystyle{ {f\left(x\right)=2x}^2+4x+4 }[/math] und [math]\displaystyle{ g\left(x\right)=-2x }[/math]. Wir setzen die Funktionen gleich und rechnen
[math]\displaystyle{ {2x}^2+4x+4=-2x\ |+2x }[/math]
[math]\displaystyle{ {2x}^2+6x+4=0~|~:2 }[/math]
[math]\displaystyle{ x^2+3x+2=0 }[/math]
damit wir die p-q-Formel anwenden können. Es gilt [math]\displaystyle{ p=3 }[/math] und [math]\displaystyle{ q=2 }[/math]. Diese Werte können wir in die p-q-Formel einsetzen:
[math]\displaystyle{ x_1=-\frac{3}{2}+\sqrt{\left(\frac{3}{2}\right)^2-2}=-1,5+\sqrt{0,25}=-1 }[/math]
und
[math]\displaystyle{ x_2=-\frac{3}{2}-\sqrt{\left(\frac{3}{2}\right)^2-2}=-1,5-\sqrt{0,25}=-2 }[/math]
Die y-Werte berechnen wir durch [math]\displaystyle{ g\left(-1\right)=-2\cdot\left(-1\right)=2 }[/math] und [math]\displaystyle{ g\left(-2\right)=-2\cdot\left(-2\right)=4 }[/math]. Die Schnittpunkte sind damit [math]\displaystyle{ A(-1|2) }[/math] und [math]\displaystyle{ B(-2|4) }[/math].
Zwei Parabeln ohne Schnittpunkt
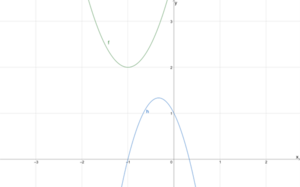
Betrachten wir zwei Parabeln, treten die gleichen drei Fälle wie oben auf. Wir betrachten hier nur den Fall, bei dem die Parabeln keine Schnittpunkte haben.
Wir betrachten [math]\displaystyle{ {f\left(x\right)=2x}^2+4x+4 }[/math] und [math]\displaystyle{ {h\left(x\right)=-3x}^2-2x+1 }[/math]. Gleichsetzen der Funktionen liefert
[math]\displaystyle{ h(x)=f(x) }[/math]
[math]\displaystyle{ -3x^2-2x+1=2x^2+4x+4~|~-2x^2 }[/math]
[math]\displaystyle{ {-5x}^2-2x+1=4x+4~|~-4x }[/math]
[math]\displaystyle{ {-5x}^2-6x+1=4~|~-4 }[/math]
[math]\displaystyle{ {-5x}^2-6x-3=0~|~:(-5) }[/math]
[math]\displaystyle{ x^2+1,2x+0,6=0 }[/math]
Es gilt [math]\displaystyle{ p=1,2 }[/math] und [math]\displaystyle{ q=0,6 }[/math].
Diese Werte können wir einsetzen:
[math]\displaystyle{ x=-\frac{1,2}{2}\pm\sqrt{\left(\frac{1,2}{2}\right)^2-0,6}=-0,6\pm\sqrt{-0,24} }[/math]
Der Wert unter der Wurzel ist negativ und damit existiert kein Schnittpunkt.