Menge: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „==Definition== ==Teilmenge== ===Mengenoperationen=== A, B seien Mengen, dann enthält <math>A \cup B</math> (A vereinigt B) alle Elemente, die in A oder in B enthalten sind. <math>A \cap B </math> (A geschnitten B) enthält alle Elemente, die in A und in B enthalten sind. <math>A \setminus B</math> (A ohne B) enthält alle Elemente, die in A und nicht in B enthalten sind. Bei einem Zufallsexperiment seien A, B Ereignisse. Dann gilt: <math>P\left(A\ \ca…“ |
Keine Bearbeitungszusammenfassung |
||
| (11 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Eine Menge ist eine Sammlung von klar definierten, unterscheidbaren Objekten, die als ihre Elemente bezeichnet werden. Diese Elemente können alles Mögliche sein, z. B. Zahlen, Buchstaben, Punkte im Raum, andere Mengen usw. | |||
==Definition== | ==Definition== | ||
Eine '''Menge''' <math>M</math> ist eine Zusammenfassung ''unterschiedlicher'' Objekte <math>x</math>. Die Objekte heißen '''Elemente''' der Menge <math>M</math>. Eine Menge wird durch Aufzählung ihrer Elemente oder durch die Angabe einer Eigenschaft beschrieben: | |||
*<math>M_1=\{x_1;...;x_n\}</math> (Aufzählung der Elemente) | |||
*<math>M_2=\{x~|~E(x)\}</math> (Alle <math>x</math>, die Bedingung <math>E(x)</math> erfüllen) | |||
Die Klammern {} heißen '''Mengenklammern'''. Das Semikolon trennt die Elemente innerhalb der Mengenklammern. Ist <math>x</math> Element der Menge <math>M</math> schreiben wir <math>x \in M</math>. Ist <math>y</math> kein Element der Menge <math>M</math> schreiben wir <math>y \notin M</math>. | |||
==Leere Menge== | |||
Die Menge, die kein Element enthält heißt '''leere Menge'''. Wir schreiben <math>\emptyset</math>. | |||
==Teilmenge== | ==Teilmenge== | ||
<math>M_1</math> und <math>M_2</math> seien Mengen. Gilt für alle <math>x \in M_1</math> auch <math>x \in M_2</math>, dann ist <math>M_1</math> eine '''Teilmenge''' von <math>M_2</math> und wir schreiben <math>M_1 \subseteq M_2</math>. Existiert zusätzlich ein <math>y \in M_2</math> mit <math>y \notin M_1</math>, dann ist <math>M_1</math> eine '''echte Teilmenge''' von <math>M_2</math> und wir schreiben <math>M_1 \subset M_2</math>. | |||
==Mengenoperationen== | |||
<math>M_1,~M_2</math> seien Mengen. In den unteren Bildern ist <math>M_1</math> durch den linken Kreis und <math>M_2</math> durch den rechten Kreis veranschaulicht. Die Mengen können vereinigt, geschnitten oder subtrahiert werden. | |||
<gallery> | |||
Datei:MengeVereinigungsmenge.png|Vereinigungsmenge | |||
MengeSchnittmenge.png|Schnittmenge | |||
Datei:MengeDifferenzmenge.png|Differenzmenge | |||
</gallery> | |||
===Vereinigungsmenge=== | |||
Die Menge <math>V=\{x~|~x \in M_1 \text{ oder } x \in M_2\}</math> heißt '''Vereinigungsmenge''' von <math>M_1</math> und <math>M_2</math>. Wir schreiben <math>V=M_1 \cup M_2</math> und sagen <math>M_1</math> '''vereinigt''' <math>M_2</math>. | |||
===Schnittmenge=== | |||
Die Menge <math>S=\{x~|~x \in M_1 \text{ und } x \in M_2\}</math> heißt '''Schnittmenge''' von <math>M_1</math> und <math>M_2</math>. Wir schreiben <math>S=M_1 \cap M_2</math> und sagen <math>M_1</math> '''geschnitten''' <math>M_2</math>. | |||
===Differenzmenge=== | |||
Die Menge <math>D=\{x~|~x \in M_1 \text{ und } x \notin M_2\}</math> heißt '''Differenzmenge''' von <math>M_1</math> und <math>M_2</math>. Wir schreiben <math>S=M_1 \backslash M_2</math> und sagen <math>M_1</math> '''minus''' <math>M_2</math>. | |||
< | <html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/Kq4Fx9Abh_s?si=Gwu3WqcPyRCzCcmG" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | ||
[[Kategorie:Wahrscheinlichkeitsrechnung]] | |||
[[Kategorie:FHR_WuV_Mathe]] | |||
[[Kategorie:AHR_WuV_Mathe_GK]] | |||
Aktuelle Version vom 3. April 2025, 07:46 Uhr
Eine Menge ist eine Sammlung von klar definierten, unterscheidbaren Objekten, die als ihre Elemente bezeichnet werden. Diese Elemente können alles Mögliche sein, z. B. Zahlen, Buchstaben, Punkte im Raum, andere Mengen usw.
Definition
Eine Menge [math]\displaystyle{ M }[/math] ist eine Zusammenfassung unterschiedlicher Objekte [math]\displaystyle{ x }[/math]. Die Objekte heißen Elemente der Menge [math]\displaystyle{ M }[/math]. Eine Menge wird durch Aufzählung ihrer Elemente oder durch die Angabe einer Eigenschaft beschrieben:
- [math]\displaystyle{ M_1=\{x_1;...;x_n\} }[/math] (Aufzählung der Elemente)
- [math]\displaystyle{ M_2=\{x~|~E(x)\} }[/math] (Alle [math]\displaystyle{ x }[/math], die Bedingung [math]\displaystyle{ E(x) }[/math] erfüllen)
Die Klammern {} heißen Mengenklammern. Das Semikolon trennt die Elemente innerhalb der Mengenklammern. Ist [math]\displaystyle{ x }[/math] Element der Menge [math]\displaystyle{ M }[/math] schreiben wir [math]\displaystyle{ x \in M }[/math]. Ist [math]\displaystyle{ y }[/math] kein Element der Menge [math]\displaystyle{ M }[/math] schreiben wir [math]\displaystyle{ y \notin M }[/math].
Leere Menge
Die Menge, die kein Element enthält heißt leere Menge. Wir schreiben [math]\displaystyle{ \emptyset }[/math].
Teilmenge
[math]\displaystyle{ M_1 }[/math] und [math]\displaystyle{ M_2 }[/math] seien Mengen. Gilt für alle [math]\displaystyle{ x \in M_1 }[/math] auch [math]\displaystyle{ x \in M_2 }[/math], dann ist [math]\displaystyle{ M_1 }[/math] eine Teilmenge von [math]\displaystyle{ M_2 }[/math] und wir schreiben [math]\displaystyle{ M_1 \subseteq M_2 }[/math]. Existiert zusätzlich ein [math]\displaystyle{ y \in M_2 }[/math] mit [math]\displaystyle{ y \notin M_1 }[/math], dann ist [math]\displaystyle{ M_1 }[/math] eine echte Teilmenge von [math]\displaystyle{ M_2 }[/math] und wir schreiben [math]\displaystyle{ M_1 \subset M_2 }[/math].
Mengenoperationen
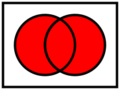
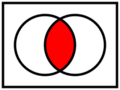
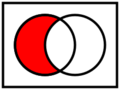
[math]\displaystyle{ M_1,~M_2 }[/math] seien Mengen. In den unteren Bildern ist [math]\displaystyle{ M_1 }[/math] durch den linken Kreis und [math]\displaystyle{ M_2 }[/math] durch den rechten Kreis veranschaulicht. Die Mengen können vereinigt, geschnitten oder subtrahiert werden.
-
Vereinigungsmenge
-
Schnittmenge
-
Differenzmenge
Vereinigungsmenge
Die Menge [math]\displaystyle{ V=\{x~|~x \in M_1 \text{ oder } x \in M_2\} }[/math] heißt Vereinigungsmenge von [math]\displaystyle{ M_1 }[/math] und [math]\displaystyle{ M_2 }[/math]. Wir schreiben [math]\displaystyle{ V=M_1 \cup M_2 }[/math] und sagen [math]\displaystyle{ M_1 }[/math] vereinigt [math]\displaystyle{ M_2 }[/math].
Schnittmenge
Die Menge [math]\displaystyle{ S=\{x~|~x \in M_1 \text{ und } x \in M_2\} }[/math] heißt Schnittmenge von [math]\displaystyle{ M_1 }[/math] und [math]\displaystyle{ M_2 }[/math]. Wir schreiben [math]\displaystyle{ S=M_1 \cap M_2 }[/math] und sagen [math]\displaystyle{ M_1 }[/math] geschnitten [math]\displaystyle{ M_2 }[/math].
Differenzmenge
Die Menge [math]\displaystyle{ D=\{x~|~x \in M_1 \text{ und } x \notin M_2\} }[/math] heißt Differenzmenge von [math]\displaystyle{ M_1 }[/math] und [math]\displaystyle{ M_2 }[/math]. Wir schreiben [math]\displaystyle{ S=M_1 \backslash M_2 }[/math] und sagen [math]\displaystyle{ M_1 }[/math] minus [math]\displaystyle{ M_2 }[/math].