Produzentenrente: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „Die '''Produzentenrente''' beschreibt den Vorteil, den ein Produzent erhält, wenn er ein Gut zu einem höheren Preis verkauft, als er bereit wäre, es anzubieten. Sie ist ein Maß für den zusätzlichen Gewinn, den Produzenten durch den Marktpreis erzielen. ==Definition== Die Produzentenrente entsteht in einem Polypol unter vollständiger Konkurrenz, in dem der Gleichgewichtspreis du…“ |
|||
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
* <math>p_m</math> der Marktpreis (Gleichgewichtspreis), | * <math>p_m</math> der Marktpreis (Gleichgewichtspreis), | ||
* <math>x_m</math> die Gleichgewichtsmenge ist. | * <math>x_m</math> die Gleichgewichtsmenge ist. | ||
<html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/S7SGSLcbhzk?si=j5bPr4smNslHxdHf" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" referrerpolicy="strict-origin-when-cross-origin" allowfullscreen></iframe></html> | |||
==Beispiele== | ==Beispiele== | ||
===Produzentenrente für eine lineare Angebotsfunktion=== | |||
[[Datei:ProduzentenrenteKonsumentenrente.png|mini|Marktgleichewgicht, Produzenten- und Konsumentenrente für lineare Funktionen]] | |||
Wir betrachten die nebenstehende Grafik. Die Angebotsfunktion ist <math>p_A(x)=\frac{1}{3}\cdot x +1 </math> und die Nachfragefunktion ist <math>p_N(x)=-x+9</math>. Das Markgleichgewicht ist <math>MGG(6|3)</math>. Die Produzentenrente ist der Gewinn, den die Produzenten dadurch erzielen, dass der Gleichgewichtspreis über den Stückkosten liegt. Die Produzentenrente ist die Fläche zwischen dem Gleichgewichtspreis und der Angebotsfunktion: <math> \text{PR} = \frac{1}{2} \cdot (3 - 1) \cdot 6 = 6 </math> | |||
===Produzentenrente berechnen=== | ===Produzentenrente berechnen=== | ||
Betrachten wir ein Beispiel mit der Angebotsfunktion <math>p_A(x) = \frac{1}{2}x + 2</math> und dem Marktpreis <math>p_m = 6</math>. Die Gleichgewichtsmenge ergibt sich, wenn die Angebotsfunktion den Marktpreis schneidet: | Betrachten wir ein Beispiel mit der Angebotsfunktion <math>p_A(x) = \frac{1}{2}x + 2</math> und dem Marktpreis <math>p_m = 6</math>. Die Gleichgewichtsmenge ergibt sich, wenn die Angebotsfunktion den Marktpreis schneidet: | ||
Aktuelle Version vom 25. Januar 2025, 09:51 Uhr
Die Produzentenrente beschreibt den Vorteil, den ein Produzent erhält, wenn er ein Gut zu einem höheren Preis verkauft, als er bereit wäre, es anzubieten. Sie ist ein Maß für den zusätzlichen Gewinn, den Produzenten durch den Marktpreis erzielen.
Definition
Die Produzentenrente entsteht in einem Polypol unter vollständiger Konkurrenz, in dem der Gleichgewichtspreis durch Angebot und Nachfrage bestimmt wird. Formal wird sie durch die Fläche über der Angebotsfunktion und unterhalb des Marktpreises bis zur Gleichgewichtsmenge dargestellt.
Die Produzentenrente [math]\displaystyle{ PR }[/math] lässt sich mathematisch berechnen als: [math]\displaystyle{ PR = p_m \cdot x_m - \int_{0}^{x_m} p_A(x) \, dx }[/math],
wobei:
- [math]\displaystyle{ p_A(x) }[/math] die Angebotsfunktion,
- [math]\displaystyle{ p_m }[/math] der Marktpreis (Gleichgewichtspreis),
- [math]\displaystyle{ x_m }[/math] die Gleichgewichtsmenge ist.
Beispiele
Produzentenrente für eine lineare Angebotsfunktion
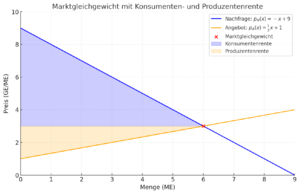
Wir betrachten die nebenstehende Grafik. Die Angebotsfunktion ist [math]\displaystyle{ p_A(x)=\frac{1}{3}\cdot x +1 }[/math] und die Nachfragefunktion ist [math]\displaystyle{ p_N(x)=-x+9 }[/math]. Das Markgleichgewicht ist [math]\displaystyle{ MGG(6|3) }[/math]. Die Produzentenrente ist der Gewinn, den die Produzenten dadurch erzielen, dass der Gleichgewichtspreis über den Stückkosten liegt. Die Produzentenrente ist die Fläche zwischen dem Gleichgewichtspreis und der Angebotsfunktion: [math]\displaystyle{ \text{PR} = \frac{1}{2} \cdot (3 - 1) \cdot 6 = 6 }[/math]
Produzentenrente berechnen
Betrachten wir ein Beispiel mit der Angebotsfunktion [math]\displaystyle{ p_A(x) = \frac{1}{2}x + 2 }[/math] und dem Marktpreis [math]\displaystyle{ p_m = 6 }[/math]. Die Gleichgewichtsmenge ergibt sich, wenn die Angebotsfunktion den Marktpreis schneidet:
[math]\displaystyle{ p_A(x) = p_m }[/math]
[math]\displaystyle{ \frac{1}{2}x + 2 = 6~|~-2 }[/math]
[math]\displaystyle{ \frac{1}{2}x = 4~|~\cdot 2 }[/math]
[math]\displaystyle{ x = 8 }[/math].
Die Produzentenrente ist die Fläche zwischen dem Marktpreis und der Angebotsfunktion: [math]\displaystyle{ PR = 6 \cdot 8 - \int_{0}^{8} \left(\frac{1}{2}x + 2\right) \, dx }[/math].
Berechnen wir das Integral: [math]\displaystyle{ \int \left(\frac{1}{2}x + 2\right) dx = \frac{1}{4}x^2 + 2x }[/math].
Einsetzen der Grenzen:
[math]\displaystyle{ \left[\frac{1}{4}x^2 + 2x \right]_{0}^{8} = \left(\frac{1}{4} \cdot 8^2 + 2 \cdot 8\right) - \left(\frac{1}{4} \cdot 0^2 + 2 \cdot 0\right) }[/math]
[math]\displaystyle{ = \left(16 + 16\right) - (0) = 32 }[/math].
Subtrahieren wir diesen Wert vom Rechteck unter dem Marktpreis: [math]\displaystyle{ PR = 6 \cdot 8 - 32 = 48 - 32 = 16 }[/math].
Die Produzentenrente beträgt 16 GE.
Veränderung der Produzentenrente bei Preisanpassungen
Ändert sich der Marktpreis, ändert sich auch die Produzentenrente. Beispielsweise sei der Marktpreis von [math]\displaystyle{ 6 }[/math] GE auf [math]\displaystyle{ 4 }[/math] GE pro ME gesunken. Wir berechnen die neue Produzentenrente.
Die neue Gleichgewichtsmenge ergibt sich durch:
[math]\displaystyle{ p_A(x) = 4 }[/math]
[math]\displaystyle{ \frac{1}{2}x + 2 = 4~|~-2 }[/math]
[math]\displaystyle{ \frac{1}{2}x = 2~|~\cdot 2 }[/math]
[math]\displaystyle{ x = 4 }[/math].
Die neue Produzentenrente ist: [math]\displaystyle{ PR = 4 \cdot 4 - \int_{0}^{4} \left(\frac{1}{2}x + 2\right) \, dx }[/math].
Berechnen wir das Integral:
[math]\displaystyle{ \left[\frac{1}{4}x^2 + 2x \right]_{0}^{4} = \left(\frac{1}{4} \cdot 4^2 + 2 \cdot 4\right) - \left(\frac{1}{4} \cdot 0^2 + 2 \cdot 0\right) }[/math]
[math]\displaystyle{ = \left(4 + 8\right) - (0) = 12 }[/math].
Subtrahieren wir diesen Wert vom Rechteck: [math]\displaystyle{ PR = 4 \cdot 4 - 12 = 16 - 12 = 4 }[/math].
Der Preisrückgang hat die Produzentenrente von 16 GE auf 4 GE reduziert.