Zinseszinsrechnung
Bei der Zinseszinsrechnung wird ein Anfangskapital (Geldbetrag) von einem Gläubiger über eine Laufzeit (Zeitraum) an einen Schuldner verliehen. Der Schuldner zahlt als Gegenleistung jährlich Zinsen an den Gläubiger. In der Regel werden die Zinsen dem Schuldner überlassen und in den darauffolgenden Jahren mit verzinst. Das gesamte Kapital, welches der Schuldner am Ende der Laufzeit zurückzahlen muss, heißt Endkapital.
Zinseszinsformel
Wird ein Anfangskapital [math]\displaystyle{ K(0) \in \mathbb{R}^{\geq 0} }[/math] mit einem Zinssatz von [math]\displaystyle{ p }[/math] mit [math]\displaystyle{ 0 \leq p \leq 1 }[/math] und [math]\displaystyle{ p\in \mathbb{R} }[/math] verzinst, so erhält man nach einer Laufzeit von [math]\displaystyle{ n \in \mathbb{N} }[/math] Jahren das Endkapital [math]\displaystyle{ K\left(n\right)=K\left(0\right)\cdot\left(1+p\right)^n=K\left(0\right)\cdot q^n }[/math]. Diese Formel nennen wir Zinseszinsformel. Wir nennen [math]\displaystyle{ q=1+p }[/math] auch Aufzinsungsfaktor.
Definition
Bei der Zinseszinsrechnung wird die Zinseszinsformel je nach gesuchter Größe geschickt umgestellt.
Anfangskapital
[math]\displaystyle{ K(0) }[/math] gesucht:
[math]\displaystyle{ K\left(n\right)=K\left(0\right)\cdot q^n~|~:q^n }[/math]
[math]\displaystyle{ K\left(0\right)=\frac{K\left(n\right)}{q^n} }[/math]
Zinssatz
[math]\displaystyle{ p }[/math] gesucht:
[math]\displaystyle{ K(n)=K(0)\cdot q^n\ |:K(0) }[/math]
[math]\displaystyle{ q^n=\frac{K\left(n\right)}{K\left(0\right)}~|~\sqrt[n]{~~} }[/math]
[math]\displaystyle{ q=\sqrt[n]{\frac{K\left(n\right)}{K\left(0\right)}} }[/math]
[math]\displaystyle{ q=1+p\ |\ -1 }[/math]
[math]\displaystyle{ q-1=p\ }[/math]
[math]\displaystyle{ p=\sqrt[n]{\frac{K\left(n\right)}{K\left(0\right)}}-1 }[/math]
Zum Schluss wurde das Ergebnis für q in die Formel für p eingesetzt werden.
Laufzeit
[math]\displaystyle{ n }[/math] gesucht:
[math]\displaystyle{ K(n)=K(0)\cdot q^n~|~:K(0) }[/math]
[math]\displaystyle{ q^n=\frac{K\left(n\right)}{K\left(0\right)}~|~log_q }[/math]
[math]\displaystyle{ n=log_q\left(\frac{K\left(n\right)}{K\left(0\right)}\right)=\frac{log\left(\frac{K\left(n\right)}{K\left(0\right)}\right)}{log\left(q\right)} }[/math]
Beispiele
Zinseszinsformel anwenden
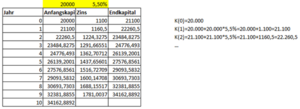
Wir legen einen Geldbetrag von 20.000 € bei einem Zinssatz von 5,5% pro Jahr für genau 10 Jahre bei einer Bank an. Wir überlassen also der Bank unser Geld und die Bank bezahlt als Gegenleistung Zinsen an uns. Es ergibt sich die rechts abgebildete Rechnung.
Wir haben also ein Anfangskapital von [math]\displaystyle{ K(0)=20.000 }[/math]€ und legen dieses Geld zu einem Zinssatz von [math]\displaystyle{ p=5,5\%=0,055 }[/math] pro Jahr an. Die Laufzeit beträgt [math]\displaystyle{ n=10 }[/math] Jahre. Nach einem Jahr erhalten wir [math]\displaystyle{ 20.000 \cdot 0,055=1100 }[/math]€ Zinsen ausgezahlt. Nach diesem Jahr besitzen wir insgesamt einen Geldbetrag von [math]\displaystyle{ 20.000+1100=21100 }[/math]€. Anschließend werden die [math]\displaystyle{ 21100 }[/math]€ verzinst, d. h. die Zinsen über [math]\displaystyle{ 1100 }[/math]€ werden mit verzinst, daher sprechen wir von Zinseszinsrechnung. Nach zwei Jahren besitzen wir einen Geldbetrag von [math]\displaystyle{ 21.100+21.100 \cdot 0,055= 22260,5 }[/math]€. Wir besitzen also nach 10 Jahren [math]\displaystyle{ K(10)\approx34.162,89 }[/math]€. Dieser Wert lässt sich auch direkt berechnen: [math]\displaystyle{ K(10)=20.000\cdot{1,055}^{10}\approx34162,89 }[/math]
Laufzeit berechnen
Wir legen ein Anfangskapital von 20.000 € zu einem Zinssatz von 5,5 % pro Jahr an. Es soll ein Endkapital über 40.000 € angespart werden. Es gilt [math]\displaystyle{ K(0)=20.000,~K(n)=40.000,~p=0,055,~q=1,055,~n=? }[/math]. Wir berechnen die dafür benötigte Laufzeit mit der Zinseszinsformel wie folgt:
[math]\displaystyle{ K(n)=K(0)\cdot q^n }[/math]
[math]\displaystyle{ 40.000=20.000\cdot 1,055^n~|~:20.000 }[/math]
[math]\displaystyle{ 2=1,055^n~|~log_{1,055} }[/math]
[math]\displaystyle{ log_{1,055}(2)=n }[/math]
[math]\displaystyle{ \frac{log(2)}{log(1,055)}=n }[/math] (Der Schritt kann alternativ angewendet werden.)
[math]\displaystyle{ 13 \approx n }[/math]
Nach ungefähr 13 Jahren beträgt das Endkapital 40.000 €.