Problem

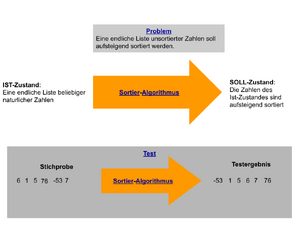
In der Informatik versteht man unter einem Problem eine Situation, in der ein Ist-Zustand nicht mit einem gewünschten Soll-Zustand übereinstimmt und diese Diskrepanz mit Hilfe eines Algorithmus gelöst werden soll. Die Existenz von Problemen und deren Lösung durch Algorithmen beschränkt sich jedoch nicht auf die Informatik.

Grundlegendes Konzept

Ein Problem liegt vor, wenn eine Lücke zwischen einer gegebenen und einer gewünschten Situation geschlossen werden muss. Lösungswege für Probleme können zunächst in der realen Welt analysiert und geplant, dann in einem Algorithmus beschrieben und schließlich in ein Computerprogramm übertragen werden. Ein historisches Beispiel ist das Verteilen von Briefen auf Zustellbezirke und Haushalte, das bereits vor der Entwicklung der Informatik gelöst wurde.

Merkmale von Problemen

Probleme lassen sich anhand verschiedener Merkmale charakterisieren.

Lösbarkeit

Nicht alle Probleme sind lösbar. Eine scheinbare Unlösbarkeit geht oft auf eine mangelhafte Problembeschreibung zurück, bei der Ist-Zustand, Soll-Zustand oder Hindernisse nicht klar formuliert sind. Jedoch kann auch für präzise formulierte Probleme in definierten Regelumgebungen mathematisch bewiesen werden, dass sie unlösbar sind. Ein klassisches Beispiel ist die Quadratur des Kreises. Die Investition von Arbeitsaufwand in erwiesenermaßen unlösbare Probleme ist nicht sinnvoll.

Zerlegbarkeit

Ein Problem gilt als zerlegbar, wenn es in mehrere Unterprobleme aufgeteilt werden kann. Diese sind oft einfacher und mit geringerem Aufwand zu lösen. Das Zerlegen komplexer Probleme ist häufig ein zentraler Lösungsschritt und wird nach dem Prinzip „Divide and Conquer“ (deutsch: „Teile und herrsche“) bezeichnet. Stellt die Zerlegung selbst ein schwieriges Problem dar, ein Problem sich überhaupt nicht unterteilen lässt oder die entstehenden Unterprobleme stets ebenso komplex wie das Ausgangsproblem sind, so wird das Problem als nicht zerlegbar oder elementar bezeichnet.

Verwandtheit

Manche Probleme sind eng miteinander verwandt. Die Lösung eines Problems kann gleichzeitig ein anderes Problem lösen, wenn deren Ist- und Soll-Situationen übereinstimmen, auch wenn sie unterschiedlich formuliert sind. Ein Problem lässt sich in ein anderes überführen. In diesem Zusammenhang spricht man von Problemklassen. Ein Lösungsansatz für ein Problem einer Klasse gilt für alle Instanzen (Ausprägungen) dieser Klasse. Auf diese Weise können ganze, noch ungelöste Problemklassen identifiziert werden. Kann ein Problem nicht auf andere zurückgeführt werden, bildet es eine eigene Problemklasse.

Lösungsaufwand

Probleme können nach dem erforderlichen Lösungsaufwand beurteilt werden. Der Lösungsweg kann kurz sein oder so aufwändig, dass der Nutzen den Aufwand nicht rechtfertigt. Extrem aufwändige Probleme können theoretisch lösbar, in der Praxis jedoch aufgrund unbegrenzt langer Lösungswege als „unlösbar“ gelten. Der benötigte Aufwand hängt von der Komplexität des Problems und der Leistungsfähigkeit des ausführenden Systems ab.

Problemspezifikation

Um Probleme algorithmisch lösen zu können, müssen sie präzise beschrieben werden. Diese Beschreibung findet im Softwareentwicklungsprozess während der Anforderungsanalyse statt. Folgende Aspekte sind zu berücksichtigen:

Ist-Zustand: Beschreibung eines gültigen Ausgangszustands, auf den das Problem anzuwenden ist.

Soll-Zustand: Beschreibung des zu erreichenden Zielzustands.

Vollständigkeit: Beschreibung aller geltenden Rahmenbedingungen und einzuhaltenden Regeln.

Detailliertheit: Beschreibung der erlaubten Funktionen und Hilfsmittel.

Eindeutigkeit: Die Gesamtbeschreibung muss eindeutig sein. Der Erfolg der Lösung muss anhand klarer Kriterien überprüfbar sein.