Ableitungsfunktion
Ableitung und Steigung in einem Punkt
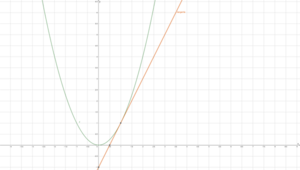
Ist [math]\displaystyle{ f }[/math] eine Funktion, die auf dem Intervall [math]\displaystyle{ [x_0;x_1] \subseteq \mathbb{D}_f }[/math] definiert ist, und strebt der Differenzenquotient [math]\displaystyle{ \frac{f\left(x\right)-f(x_0)}{x-x_0} }[/math] für [math]\displaystyle{ x\rightarrow x_0 }[/math] und [math]\displaystyle{ x \in [x_0;x_1] }[/math] gegen einen Wert, so heißt dieser Wert Ableitung (lokale Änderungsrate) von [math]\displaystyle{ f }[/math] an der Stelle [math]\displaystyle{ x_0 }[/math] und wird mit [math]\displaystyle{ f'(x_0) }[/math] bezeichnet. [math]\displaystyle{ f }[/math] heißt an der Stelle [math]\displaystyle{ x_0 }[/math] differenzierbar.
Die Ableitung ist die Steigung der Tangente im Punkt [math]\displaystyle{ {P(x}_0|f\left(x_0\right)) }[/math] und heißt Steigung des Graphen von [math]\displaystyle{ f }[/math] in [math]\displaystyle{ P }[/math].
Definition
Ist eine Funktion [math]\displaystyle{ f }[/math] für alle [math]\displaystyle{ x\ \in\ \mathbb{D}_f }[/math] differenzierbar, so heißt die Funktion [math]\displaystyle{ f' }[/math], die jeder Stelle [math]\displaystyle{ x }[/math] der Definitionsmenge die Ableitung [math]\displaystyle{ f'(x) }[/math] zuordnet, Ableitungsfunktion. Wir bezeichnen [math]\displaystyle{ f' }[/math] auch als Ableitung von [math]\displaystyle{ f }[/math].
Ableitungsregeln
Die Ableitungsfunktion [math]\displaystyle{ f' }[/math] wird mit den folgenden Regeln ermittelt:
Potenzregel
Die Funktion [math]\displaystyle{ f\left(x\right)=x^n }[/math] hat die Ableitungsfunktion [math]\displaystyle{ f'\left(x\right)=n{\cdot x}^{n-1} }[/math] für [math]\displaystyle{ n\ \in\mathbb{N} }[/math].
Faktorregel
Für [math]\displaystyle{ f\left(x\right)=c\cdot g(x) }[/math] gilt [math]\displaystyle{ f'\left(x\right)=c\cdot g'(x) }[/math].
Summenregel
Für [math]\displaystyle{ f\left(x\right)=g\left(x\right)+h(x) }[/math] gilt [math]\displaystyle{ f'\left(x\right)=g'\left(x\right)+h'(x) }[/math].
Beispiele
Steigung in einem Punkt mit Hilfe der Tangente ermitteln
Wir betrachten [math]\displaystyle{ f\left(x\right)=x^2 }[/math] im Punkt [math]\displaystyle{ P(1|1) }[/math]. Die Tangente in diesem Punkt ist [math]\displaystyle{ t\left(x\right)=2x-1 }[/math]. Die Steigung von [math]\displaystyle{ f }[/math] in [math]\displaystyle{ P }[/math] ist [math]\displaystyle{ 2 }[/math].
Potenz-, Faktor- und Summenregel anwenden
Wendet man auf [math]\displaystyle{ f\left(x\right)=x^6 }[/math] die Potenzregel an, gilt [math]\displaystyle{ f'\left(x\right)=6x^{6-1}=6x^5 }[/math]. Die Steigung im Punkt [math]\displaystyle{ P(1|2) }[/math] ist dann [math]\displaystyle{ f'(1)=6 \cdot 1^5=6 }[/math].
Wendet man auf [math]\displaystyle{ g\left(x\right)=3x^5 }[/math] die Faktorregel an, gilt [math]\displaystyle{ g'\left(x\right)=3\cdot5x^{5-1}=15x^4 }[/math].
Wendet man auf [math]\displaystyle{ h\left(x\right)=2x^3+3x^4 }[/math] die Summenregel an, gilt [math]\displaystyle{ h'(x)=2\cdot3x^2+4\cdot3x^3=6x^2+12x^3 }[/math]. Das dritte Video zeigt, wie Ableitungsfunktionen skizziert werden können.
Höhere Ableitungen ermitteln
Höhere Ableitungen werden durch mehrmaliges Anwenden der Ableitungsregeln angewendet. Die Ableitungsfunktion von [math]\displaystyle{ f'(x) }[/math] ist dann [math]\displaystyle{ f''(x) }[/math] und die Ableitungsfunktion von [math]\displaystyle{ f''(x) }[/math] ist [math]\displaystyle{ f'''(x) }[/math]. [math]\displaystyle{ f''(x) }[/math] bzw. [math]\displaystyle{ f'''(x) }[/math] bezeichnen wir mit zweite bzw. dritte Ableitung.