Gewinnfunktion: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „Bei der Gewinnanalyse werden Erlöse, Kosten und Gewinne für ein Produkt mit Hilfe von Funktionen modelliert, graphisch dargestellt und untersucht. ==Gewinnfunktion== Eine Funktion, die jeder Produktionsmenge <math>x</math> den Gewinn <math>G(x)</math> zuordnet, heißt '''Gewinnfunktion'''. Dabei ist wie zuvor <math>x \in[0;x_{max}]</math>. Der Gewinn ist die Differenz aus Erlös und Kosten: <math>G\left(x\right)=E\left(x\right)-K(x)</math> ===Beispie…“ |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
Mit Hilfe einer Gewinnfunktion wird der Gewinn für eine bestimmte Produktionsmenge ermittelt. Der Gewinn berechnet sich durch Erlös minus Kosten. | |||
== | ==Definition== | ||
Eine Funktion, die jeder Produktionsmenge <math>x</math> den Gewinn <math>G(x)</math> zuordnet, heißt '''Gewinnfunktion'''. Dabei ist wie zuvor <math>x \in[0;x_{max}]</math>. Der Gewinn ist die Differenz aus Erlös und Kosten: <math>G\left(x\right)=E\left(x\right)-K(x)</math> | Eine Funktion, die jeder Produktionsmenge <math>x</math> den Gewinn <math>G(x)</math> zuordnet, heißt '''Gewinnfunktion'''. Dabei ist wie zuvor <math>x \in[0;x_{max}]</math>. Der Gewinn ist die Differenz aus Erlös und Kosten: <math>G\left(x\right)=E\left(x\right)-K(x)</math> | ||
=== | <html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/aQ0J7uPZDJ0?si=gQsaFaVl-BBUPUfA" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | ||
==Gewinnschwelle, Gewinngrenze und Gewinnzone== | |||
Die '''Gewinnschwelle''' <math>x_s</math> ist die kleinste Produktionsmenge, für die der Gewinn gleich 0 ist. Die '''Gewinngrenze''' <math>x_g</math> ist die größte Produktionsmenge, für die der Gewinn gleich 0 ist. In der '''Gewinnzone''', <math>[x_s;x_g]</math>, liegen die Produktionsmengen, für die der Gewinn nicht negativ ist. Die Gewinnschwelle und die Gewinngrenze werden durch <math>K(x)=E(x)</math> oder <math>G\left(x\right)=E\left(x\right)-K(x)=0</math> berechnet. Sie sind also Nullstellen der Gewinnfunktion. Eine lineare Gewinnfunktion hat nur eine Gewinnschwelle und keine Gewinngrenze, da der Graph eine Gerade ist. | |||
==Break-Even-Point (BEP) für lineare Funktionen== | |||
Für eine lineare Gewinnfunktion heißt der Punkt <math>S(x_s| E(x_s))</math> '''Break-Even-Point (BEP)'''. Im BEP sind also Kosten und Erlös gleich. | |||
==Beispiele== | |||
===Eine lineare Gewinnfunktion herleiten und analysieren=== | |||
Die Produktion von Fahrrädern verursacht fixe Kosten von 2700 €. Die variablen Stückkosten betragen 18 € pro Fahrrad. Die Produzierten Fahrräder werden für jeweils 300 € pro Stück verkauft. Die Kapazitätsgrenze beträgt 30 Stück. Wie hoch ist der Gewinn, falls die Kapazitätsgrenze erreicht wird? | Die Produktion von Fahrrädern verursacht fixe Kosten von 2700 €. Die variablen Stückkosten betragen 18 € pro Fahrrad. Die Produzierten Fahrräder werden für jeweils 300 € pro Stück verkauft. Die Kapazitätsgrenze beträgt 30 Stück. Wie hoch ist der Gewinn, falls die Kapazitätsgrenze erreicht wird? | ||
Für die Kostenfunktion gilt <math>K(x)=18x\ +2700</math> mit <math>K_v=18</math> und <math>K_f=2700</math>. Weil der Erlös pro Einheit 300 € beträgt, ist <math>E_v=300</math> und die Erlösfunktion <math>E(x)=300x</math>. Die Gewinnfunktion ist also <math>G\left(x\right)=E\left(x\right)-K\left(x\right)=300x\ -\left(18x\ +2700\right)=282x-2700</math>. Also ist der Gewinn für die Kapazitätsgrenze <math>G(30)=282 \cdot 30-2700=5760</math> €. | Für die Kostenfunktion gilt <math>K(x)=18x\ +2700</math> mit <math>K_v=18</math> und <math>K_f=2700</math>. Weil der Erlös pro Einheit 300 € beträgt, ist <math>E_v=300</math> und die Erlösfunktion <math>E(x)=300x</math>. Die Gewinnfunktion ist also <math>G\left(x\right)=E\left(x\right)-K\left(x\right)=300x\ -\left(18x\ +2700\right)=282x-2700</math>. Also ist der Gewinn für die Kapazitätsgrenze <math>G(30)=282 \cdot 30-2700=5760</math> €. | ||
=== | ===Eine ganzrationale Gewinnfunktion herleiten=== | ||
Die variable Kostenfunktion für ein Produkt ist durch <math>K_v(x)=0,2x^3-4x^2+30x</math> gegeben. Die Fixkosten betragen 20 GE. Der Verkaufspreis pro Stück beträgt 32,8 GE. | Die variable Kostenfunktion für ein Produkt ist durch <math>K_v(x)=0,2x^3-4x^2+30x</math> gegeben. Die Fixkosten betragen 20 GE. Der Verkaufspreis pro Stück beträgt 32,8 GE. | ||
| Zeile 20: | Zeile 29: | ||
<math>G(x)=E(x)-K(x)=32,8x-(0,2x^3-4x^2+30x+20)=32,8x-0,2x^3+4x^2-30x-20=-0,2x^3+4x^2+2,8x-20</math> | <math>G(x)=E(x)-K(x)=32,8x-(0,2x^3-4x^2+30x+20)=32,8x-0,2x^3+4x^2-30x-20=-0,2x^3+4x^2+2,8x-20</math> | ||
=== | |||
===Gewinnschwelle einer linearen Funktion ermitteln=== | |||
Für die Gewinnfunktion <math>G\left(x\right)=282x-2700</math> gilt | Für die Gewinnfunktion <math>G\left(x\right)=282x-2700</math> gilt | ||
| Zeile 34: | Zeile 42: | ||
für die Gewinnschwelle. | für die Gewinnschwelle. | ||
=== | ===Gewinnschwelle, Gewinngrenze und Gewinnzone einer ganzrationalen Funktion berechnen mit graphischer Darstellung=== | ||
[[Datei:GewinnanalyseGraphGewinnfunktion.png|mini|Graph der Gewinnfunktion <math>G(x)=-0,2x^3+4x^2-30x-20</math>]] | [[Datei:GewinnanalyseGraphGewinnfunktion.png|mini|Graph der Gewinnfunktion <math>G(x)=-0,2x^3+4x^2-30x-20</math>]] | ||
Die Gewinnfunktion für ein Produkt ist durch <math>G(x)=-0,2x^3+4x^2+2,8x-20</math> gegeben. x ist die Menge in ME und G(x) gibt den Gewinn in GE an. | Die Gewinnfunktion für ein Produkt ist durch <math>G(x)=-0,2x^3+4x^2+2,8x-20</math> gegeben. x ist die Menge in ME und G(x) gibt den Gewinn in GE an. | ||
| Zeile 54: | Zeile 62: | ||
Beispielsweise gilt <math>G(4)=-0,2\cdot 2^3+4\cdot 2^2+2,8\cdot 2-20=42,4</math>. Wir zeichnen die Punkte dann in ein Koordinatensystem ein, verbinden diese und erhalten den Graph auf der rechten Seite. | Beispielsweise gilt <math>G(4)=-0,2\cdot 2^3+4\cdot 2^2+2,8\cdot 2-20=42,4</math>. Wir zeichnen die Punkte dann in ein Koordinatensystem ein, verbinden diese und erhalten den Graph auf der rechten Seite. | ||
== | ===Break-Even-Point für eine lineare Funktion ermitteln=== | ||
Für die Gewinnfunktion <math>G\left(x\right)=282x-2700</math> mit <math>K(x)=18x+2700</math> und <math>E(x)=300x</math> ist <math>x \approx 9,57</math> die Gewinnschwelle (siehe Beispiel Gewinnschwelle). Der Break-Even-Point ergibt sich durch Einsetzen in die Erlösfunktion <math>E(9,57)\approx300\cdot 9,57\approx2872,34</math> und ist damit <math>S(9,57|2872,34)</math>. Alternativ können die Erlösfunktion und die Kostenfunktion gleichgesetzt werden: | Für die Gewinnfunktion <math>G\left(x\right)=282x-2700</math> mit <math>K(x)=18x+2700</math> und <math>E(x)=300x</math> ist <math>x \approx 9,57</math> die Gewinnschwelle (siehe Beispiel Gewinnschwelle). Der Break-Even-Point ergibt sich durch Einsetzen in die Erlösfunktion <math>E(9,57)\approx300\cdot 9,57\approx2872,34</math> und ist damit <math>S(9,57|2872,34)</math>. Alternativ können die Erlösfunktion und die Kostenfunktion gleichgesetzt werden: | ||
| Zeile 69: | Zeile 74: | ||
Der Term im letzten Rechenschritt entspricht genau der Gewinnfunktion. Die restliche Rechnung läuft dann analog zu oben. | Der Term im letzten Rechenschritt entspricht genau der Gewinnfunktion. Die restliche Rechnung läuft dann analog zu oben. | ||
[[Kategorie:Mathematische]] | [[Kategorie:Mathematische]] | ||
[[Kategorie:Gewinnanalyse]] | [[Kategorie:Gewinnanalyse]] | ||
[[Kategorie:Fachabitur]] | [[Kategorie:Fachabitur]] | ||
Version vom 14. Juli 2024, 09:53 Uhr
Mit Hilfe einer Gewinnfunktion wird der Gewinn für eine bestimmte Produktionsmenge ermittelt. Der Gewinn berechnet sich durch Erlös minus Kosten.
Definition
Eine Funktion, die jeder Produktionsmenge [math]\displaystyle{ x }[/math] den Gewinn [math]\displaystyle{ G(x) }[/math] zuordnet, heißt Gewinnfunktion. Dabei ist wie zuvor [math]\displaystyle{ x \in[0;x_{max}] }[/math]. Der Gewinn ist die Differenz aus Erlös und Kosten: [math]\displaystyle{ G\left(x\right)=E\left(x\right)-K(x) }[/math]
Gewinnschwelle, Gewinngrenze und Gewinnzone
Die Gewinnschwelle [math]\displaystyle{ x_s }[/math] ist die kleinste Produktionsmenge, für die der Gewinn gleich 0 ist. Die Gewinngrenze [math]\displaystyle{ x_g }[/math] ist die größte Produktionsmenge, für die der Gewinn gleich 0 ist. In der Gewinnzone, [math]\displaystyle{ [x_s;x_g] }[/math], liegen die Produktionsmengen, für die der Gewinn nicht negativ ist. Die Gewinnschwelle und die Gewinngrenze werden durch [math]\displaystyle{ K(x)=E(x) }[/math] oder [math]\displaystyle{ G\left(x\right)=E\left(x\right)-K(x)=0 }[/math] berechnet. Sie sind also Nullstellen der Gewinnfunktion. Eine lineare Gewinnfunktion hat nur eine Gewinnschwelle und keine Gewinngrenze, da der Graph eine Gerade ist.
Break-Even-Point (BEP) für lineare Funktionen
Für eine lineare Gewinnfunktion heißt der Punkt [math]\displaystyle{ S(x_s| E(x_s)) }[/math] Break-Even-Point (BEP). Im BEP sind also Kosten und Erlös gleich.
Beispiele
Eine lineare Gewinnfunktion herleiten und analysieren
Die Produktion von Fahrrädern verursacht fixe Kosten von 2700 €. Die variablen Stückkosten betragen 18 € pro Fahrrad. Die Produzierten Fahrräder werden für jeweils 300 € pro Stück verkauft. Die Kapazitätsgrenze beträgt 30 Stück. Wie hoch ist der Gewinn, falls die Kapazitätsgrenze erreicht wird?
Für die Kostenfunktion gilt [math]\displaystyle{ K(x)=18x\ +2700 }[/math] mit [math]\displaystyle{ K_v=18 }[/math] und [math]\displaystyle{ K_f=2700 }[/math]. Weil der Erlös pro Einheit 300 € beträgt, ist [math]\displaystyle{ E_v=300 }[/math] und die Erlösfunktion [math]\displaystyle{ E(x)=300x }[/math]. Die Gewinnfunktion ist also [math]\displaystyle{ G\left(x\right)=E\left(x\right)-K\left(x\right)=300x\ -\left(18x\ +2700\right)=282x-2700 }[/math]. Also ist der Gewinn für die Kapazitätsgrenze [math]\displaystyle{ G(30)=282 \cdot 30-2700=5760 }[/math] €.
Eine ganzrationale Gewinnfunktion herleiten
Die variable Kostenfunktion für ein Produkt ist durch [math]\displaystyle{ K_v(x)=0,2x^3-4x^2+30x }[/math] gegeben. Die Fixkosten betragen 20 GE. Der Verkaufspreis pro Stück beträgt 32,8 GE.
Die Erlösfunktion, die Kostenfunktion und die Gewinnfunktion berechnen sich wie folgt:
[math]\displaystyle{ E(x)=32,8x }[/math]
[math]\displaystyle{ K(x)=K_v(x)+K_f=,2x^3-4x^2+30x+20 }[/math]
[math]\displaystyle{ G(x)=E(x)-K(x)=32,8x-(0,2x^3-4x^2+30x+20)=32,8x-0,2x^3+4x^2-30x-20=-0,2x^3+4x^2+2,8x-20 }[/math]
Gewinnschwelle einer linearen Funktion ermitteln
Für die Gewinnfunktion [math]\displaystyle{ G\left(x\right)=282x-2700 }[/math] gilt
[math]\displaystyle{ 282x-2700=0\ |+2700 }[/math]
[math]\displaystyle{ 282x=2700\ |:282 }[/math]
[math]\displaystyle{ x \approx 9,57 }[/math]
für die Gewinnschwelle.
Gewinnschwelle, Gewinngrenze und Gewinnzone einer ganzrationalen Funktion berechnen mit graphischer Darstellung
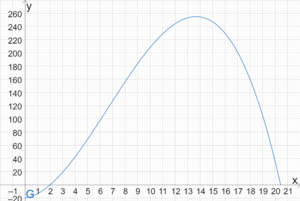
Die Gewinnfunktion für ein Produkt ist durch [math]\displaystyle{ G(x)=-0,2x^3+4x^2+2,8x-20 }[/math] gegeben. x ist die Menge in ME und G(x) gibt den Gewinn in GE an.
Wir ermitteln Gewinnschwelle, Gewinngrenze und Gewinnzone, indem wir die Nullstellen mit dem Taschenrechner berechnen:
[math]\displaystyle{ 0=-0,2x^3+4x^2+2,8x-20 }[/math]
[math]\displaystyle{ x_1 \approx -2,45, x_2=2, x_3 \approx 20,45 }[/math] Die Gewinnschwelle beträgt 2 ME, die Gewinngrenze 20,45 ME, die Gewinnzone beträgt [math]\displaystyle{ [2;20,45] }[/math] und der ökonomische Definitionsbereich beträgt [math]\displaystyle{ \mathbb{D}_{\text{ök}}=[0;20,45] }[/math]. Um den Graphen der Gewinnfunktion zu zeichnen, erstellen wir eine Wertetabelle für x-Werte in [math]\displaystyle{ \mathbb{D}_{\text{ök}} }[/math]:
| x | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 |
| G(x) | -20 | 0 | 42,4 | 97,6 | 156 | 208 | 244 | 254,4 | 229,6 | 160 | 36 | -160 |
Beispielsweise gilt [math]\displaystyle{ G(4)=-0,2\cdot 2^3+4\cdot 2^2+2,8\cdot 2-20=42,4 }[/math]. Wir zeichnen die Punkte dann in ein Koordinatensystem ein, verbinden diese und erhalten den Graph auf der rechten Seite.
Break-Even-Point für eine lineare Funktion ermitteln
Für die Gewinnfunktion [math]\displaystyle{ G\left(x\right)=282x-2700 }[/math] mit [math]\displaystyle{ K(x)=18x+2700 }[/math] und [math]\displaystyle{ E(x)=300x }[/math] ist [math]\displaystyle{ x \approx 9,57 }[/math] die Gewinnschwelle (siehe Beispiel Gewinnschwelle). Der Break-Even-Point ergibt sich durch Einsetzen in die Erlösfunktion [math]\displaystyle{ E(9,57)\approx300\cdot 9,57\approx2872,34 }[/math] und ist damit [math]\displaystyle{ S(9,57|2872,34) }[/math]. Alternativ können die Erlösfunktion und die Kostenfunktion gleichgesetzt werden:
[math]\displaystyle{ E(x)=K(x) }[/math]
[math]\displaystyle{ 300x=18x+2700\ |-18x }[/math]
[math]\displaystyle{ 300x-18x=2700\ |-2700 }[/math]
[math]\displaystyle{ 282x-2700=0 }[/math]
Der Term im letzten Rechenschritt entspricht genau der Gewinnfunktion. Die restliche Rechnung läuft dann analog zu oben.