Zinseszinsrechnung: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| Zeile 49: | Zeile 49: | ||
===Erklärvideo zum Umformen der Zinseszinsformel=== | ===Erklärvideo zum Umformen der Zinseszinsformel=== | ||
<html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/o7vwsv-Z5gw?si=oXSXuAiEy6rf_BIw" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | <html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/o7vwsv-Z5gw?si=oXSXuAiEy6rf_BIw" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | ||
[[Kategorie:Mathematik]] | |||
[[Kategorie:Finanzmathematik]] | |||
Version vom 8. Juli 2024, 09:11 Uhr
Bei der Zinseszinsrechnung wird ein Kapital (Geldbetrag) über einen Zeitraum (z. B. 5 Jahre) angelegt und verzinst (für das Anlegen erhält der Geldgeber regelmäßig einen Geldbetrag). Die Zinsen werden in der Regel jährlich ausgezahlt und wieder verzinst.
Beispiel
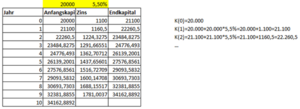
Wird ein Geldbetrag von 20000 € bei einem Zinssatz von 5,5% pro Jahr für genau 10 Jahre angelegt, ergibt sich die rechts abgebildete Rechnung.
Wir haben also zu Beginn einen Betrag von [math]\displaystyle{ K(0)=20000 }[/math]€ und legen dieses Geld für [math]\displaystyle{ 5,5\%=0,055 }[/math] pro Jahr an. Nach einem Jahr erhalten wir [math]\displaystyle{ 20000 \cdot 0,055=1100 }[/math]€ Zinsen ausgezahlt. Nach diesem Jahr besitzen wir insgesamt einen Geldbetrag von [math]\displaystyle{ 20000+1100=21100 }[/math]€. Anschließend werden die [math]\displaystyle{ 21100 }[/math]€ verzinst, d. h. die Zinsen über [math]\displaystyle{ 1100 }[/math]€ werden mit verzinst, daher sprechen wir von Zinseszinsrechnung. Nach zwei Jahren besitzen wir einen Geldbetrag von [math]\displaystyle{ 21100+21100 \cdot 0,055= 22260,5 }[/math]€. Wir besitzen also nach 10 Jahren [math]\displaystyle{ K(10)\approx34162,89 }[/math]€. Dieser Wert lässt sich auch direkt berechnen: [math]\displaystyle{ K\left(10\right)=20.000\cdot{1,055}^{10}\approx34162,89 }[/math] Das untere Video veranschaulicht eine ähnliche Rechnung mit einem Zahlenstrahl.
Zinseszinsformel
Wird ein Anfangskapital K(0) mit einem Zinssatz von p verzinst, so erhält man nach einer Laufzeit von n Jahren das Endkapital [math]\displaystyle{ K\left(n\right)=K\left(0\right)\cdot\left(1+p\right)^n=K\left(0\right)\cdot q^n }[/math]. Diese Formel nennen wir Zinseszinsformel. Wir nennen [math]\displaystyle{ q=1+p }[/math] auch Aufzinsungsfaktor.
Zinseszinsformel umformen
Die Zinseszinsformel können wir je nach gesuchter Größe geschickt umstellen:
Anfangskapital
K(0) gesucht:
[math]\displaystyle{ K\left(n\right)=K\left(0\right)\cdot q^n\ |:q^n }[/math]
[math]\displaystyle{ K\left(0\right)=\frac{K\left(n\right)}{q^n} }[/math]
Zinssatz
p gesucht:
[math]\displaystyle{ K(n)=K(0)\cdot q^n\ |:K(0) }[/math]
[math]\displaystyle{ q^n=\frac{K\left(n\right)}{K\left(0\right)}\ |\ \sqrt[n]{~~} }[/math]
[math]\displaystyle{ q=\sqrt[n]{\frac{K\left(n\right)}{K\left(0\right)}} }[/math]
[math]\displaystyle{ q=1+p\ |\ -1 }[/math]
[math]\displaystyle{ q-1=p\ }[/math]
[math]\displaystyle{ p=\sqrt[n]{\frac{K\left(n\right)}{K\left(0\right)}}-1 }[/math]
Zum Schluss wurde das Ergebnis für q in die Formel für p eingesetzt werden.
Laufzeit
n gesucht:
[math]\displaystyle{ K\left(n\right)=K\left(0\right)\cdot q^n\ |:K(0) }[/math]
[math]\displaystyle{ q^n=\frac{K\left(n\right)}{K\left(0\right)}\ |log_q }[/math]
[math]\displaystyle{ n=log_q\left(\frac{K\left(n\right)}{K\left(0\right)}\right)=\frac{log\left(\frac{K\left(n\right)}{K\left(0\right)}\right)}{log\left(q\right)} }[/math]
Erklärvideo zum Umformen der Zinseszinsformel