Funktion

Funktionen sind ein wesentlicher Bestandteil der Analysis, einem Gebiet der Mathematik. Sie haben viele praktische Anwendungen in verschiedenen Bereichen wie Wirtschaft, Ingenieurwesen, Naturwissenschaften und Sozialwissenschaften und beschreiben die Beziehung zwischen zwei Variablen und können verwendet werden, um Trends, Muster und Veränderungen im Verhalten von Phänomenen zu analysieren und vorherzusagen.

Variable

Eine Variable ist ein Name bzw. eine Bezeichnung für einen Wert oder einen mathematischen Ausdruck. Variablen werden häufig mit [math]\displaystyle{ x }[/math] oder [math]\displaystyle{ y }[/math] bezeichnet.

Beispiel: Geschwindigkeit als Variable

Wir definieren die Variable [math]\displaystyle{ x }[/math], Geschwindigkeit in km/h mit der wir fahren. [math]\displaystyle{ x=2 }[/math] bedeutet dann, dass die Geschwindigkeit mit der wir fahren [math]\displaystyle{ 2 \frac{km}{h} }[/math] beträgt. [math]\displaystyle{ x=50 }[/math] bedeutet, dass die Geschwindigkeit mit der wir fahren [math]\displaystyle{ 50 \frac{km}{h} }[/math] beträgt. Wenn wir maximal [math]\displaystyle{ 100 \frac{km}{h} }[/math] fahren können, kann [math]\displaystyle{ x }[/math] Werte zwischen [math]\displaystyle{ 0 }[/math] und [math]\displaystyle{ 100 }[/math] annehmen.

Beispiel: Preis als Variable

Wir definieren die Variable [math]\displaystyle{ y }[/math], Preis in [math]\displaystyle{ \text{€} }[/math] für Schuhe. [math]\displaystyle{ x=100 }[/math] bedeutet dann, dass der Preis für die Schuhe [math]\displaystyle{ 100 \text{€} }[/math] beträgt.

Zuordnung

Bei der mathematischen Beschreibung einer Situation („Modellierung“) hängen häufig unterschiedliche Größen voneinander ab, z. B. Preis und Menge, Weg und Zeit, Bremsweg und Geschwindigkeit. Wir sprechen dann von einer Zuordnung.

Funktion

Eine Zuordnung, die jeder Zahl [math]\displaystyle{ x }[/math] aus einer Menge genau eine reelle Zahl [math]\displaystyle{ y }[/math] zuordnet, heißt Funktion. Ein [math]\displaystyle{ x }[/math]-Wert wird auch als Stelle bezeichnet. Die einer Zahl [math]\displaystyle{ x }[/math] mittels einer Funktion [math]\displaystyle{ f }[/math] eindeutig zugeordnete Zahl [math]\displaystyle{ y }[/math] heißt Funktionswert von [math]\displaystyle{ f }[/math] an der Stelle [math]\displaystyle{ x }[/math]. Ein Punkt besteht aus [math]\displaystyle{ x }[/math]- und [math]\displaystyle{ y }[/math]-Wert, wir schreiben [math]\displaystyle{ (x|y) }[/math]. Zeichnen wir die Punkte in ein Koordinatensystem, erhalten wir den Graph der Funktion [math]\displaystyle{ f }[/math].

Definitions- und Wertebereich

Definitions- und Wertebereich aus einer Funktion ablesen

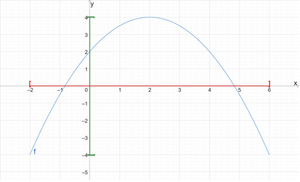
Die Menge aller [math]\displaystyle{ x }[/math]-Werte, denen durch eine Funktion [math]\displaystyle{ f }[/math] ein Funktionswert zugeordnet wird, heißt Definitionsmenge oder Definitionsbereich. Diese Menge wird meist mit [math]\displaystyle{ \mathbb{D}_f }[/math] bezeichnet. Die Menge aller Funktionswerte heißt Wertemenge oder Wertebereich und wird mit [math]\displaystyle{ \mathbb{W}_f }[/math] bezeichnet.

Beispiel

Wir betrachten den rechten Graphen:

Der Definitionsbereich von [math]\displaystyle{ 𝑓 }[/math] ist das Intervall von [math]\displaystyle{ x = -2 }[/math] bis [math]\displaystyle{ x = 6 }[/math]. Also: 𝔻𝑓 = [-2; 6].

Der Wertebereich von [math]\displaystyle{ 𝑓 }[/math] ist das Intervall von [math]\displaystyle{ y = -4 }[/math] bis [math]\displaystyle{ y = 4 }[/math]. Also: 𝕎𝑓 = [-4; 4]

Wichtige Schreibweisen

Ist eine Funktion [math]\displaystyle{ f }[/math] nicht in einem eingeschränkten Bereich, sondern für alle reellen Zahlen [math]\displaystyle{ x }[/math] definiert, schreibt man [math]\displaystyle{ \mathbb{D}_f=\mathbb{R} }[/math].

Ist eine Funktion [math]\displaystyle{ f }[/math] für alle positiven reellen Zahlen definiert, schreibt man [math]\displaystyle{ D_f=\mathbb{R}^{\gt 0} }[/math]. Wir schreiben [math]\displaystyle{ D_f=\mathbb{R}^{≥0} }[/math], wenn die Zahl [math]\displaystyle{ 0 }[/math] miteingeschlossen wird. Auch hier kann man die Intervallschreibweise verwenden: [math]\displaystyle{ (0;\infty) }[/math] bzw. [math]\displaystyle{ [0;\infty) }[/math].

Ist eine Funktion [math]\displaystyle{ f }[/math] nur für negative Zahlen definiert, schreibt man entsprechend [math]\displaystyle{ D_f=\mathbb{R}^{\lt 0} }[/math]. Wird die [math]\displaystyle{ 0 }[/math] miteingeschlossen, schreiben wir [math]\displaystyle{ D_f=\mathbb{R}^{≤0} }[/math]. In der Intervallschreibweise bedeutet dies [math]\displaystyle{ (-\infty;0) }[/math] bzw. [math]\displaystyle{ (-\infty;0] }[/math].

Beispiele

Temperatur als Zuordnung darstellen

Die folgende Tabelle zeigt eine Zuordnung, die keine Funktion ist, weil dem [math]\displaystyle{ x }[/math]-Wert 1 die beiden [math]\displaystyle{ y }[/math]-Werte [math]\displaystyle{ -1 }[/math] und [math]\displaystyle{ 5 }[/math] zugeordnet werden. In dem Monat Januar wurden also die Temperaturen -1 °C und 5 °C gemessen.

Graph von [math]\displaystyle{ f(x)=7x+2 }[/math] mit [math]\displaystyle{ A(1|9) }[/math]

x (Monat)	y (Temperatur in °C)
1	-1
1	-5
2	25

Aktienkurs als Funktion darstellen

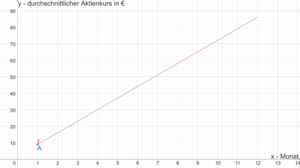
Die Variable [math]\displaystyle{ x }[/math] bezeichnet den Monat. [math]\displaystyle{ f }[/math] mit [math]\displaystyle{ f(x)=7x+2 }[/math] ist eine Funktion, weil für jeden [math]\displaystyle{ x }[/math]-Wert genau ein Funktionswert berechnet wird. Durch [math]\displaystyle{ f }[/math] wird der durchschnittliche Kurs einer Aktie in GE (Geldeinheiten) für den jeweiligen Monat berechnet werden. Der Funktionswert von [math]\displaystyle{ f }[/math] an der Stelle [math]\displaystyle{ x=1 }[/math] berechnet sich beispielsweise durch [math]\displaystyle{ f(1)=7 \cdot 1+2=9 }[/math]. Der Punkt [math]\displaystyle{ A(1|9) }[/math] liegt auf dem Graphen der Funktion [math]\displaystyle{ f }[/math]. Im Monat [math]\displaystyle{ 1 }[/math] liegt der durchschnittliche Kurs der Aktie also bei [math]\displaystyle{ 9GE }[/math]. Die [math]\displaystyle{ x }[/math]-Werte gehen nur von 1 bis 12, also gilt [math]\displaystyle{ \mathbb{D}_f=[1;12] }[/math]. Die Funktionswerte gehen von 9 bis 86, also gilt [math]\displaystyle{ \mathbb{W}_f=[1;12] }[/math] Dabei entspricht die 1 dem Januar und die 12 entspricht Dezember.

Funktionsarten und Themen

Wir unterscheiden unterschiedlich Arten von Funktionen, Themen und Anwendungen:

Lineare Funktionen

Lineare Funktionen werden verwendet, um eine Gewinnsituation zu modellieren oder um das Angebot- und Nachfrageverhalten auf Märkten zu untersuchen.