Entropie

Entropie: Das Maß für Unordnung im Datensatz

Stell dir vor, du hast eine Kiste mit Bauklötzen. Wenn alle Klötze nach Farben sortiert in Reihen liegen, herrscht in der Kiste Ordnung. Du weißt genau, wo welcher Klotz ist.

Wenn du die Kiste schüttelst, fliegen die Klötze durcheinander. Jetzt herrscht Unordnung. Es ist viel schwieriger vorherzusagen, wo ein bestimmter Klotz landet.

Genau so ist es auch mit Daten im maschinellen Lernen. Entropie ist ein Maß dafür, wie "unordentlich" oder "unsicher" unsere Daten sind, besonders wenn es um die Klassifizierung geht – also darum, Datenpunkten die richtige Kategorie zuzuordnen.

Was bedeutet "Unordnung" in Daten?

Im maschinellen Lernen betrachten wir oft Datensätze, bei denen jeder Datenpunkt zu einer bestimmten Klasse gehört. Zum Beispiel:

• Spam-Erkennung: Eine E-Mail ist entweder "Spam" oder "kein Spam".
• Bilderkennung: Ein Bild zeigt entweder eine "Katze" oder einen "Hund".

Hohe Entropie bedeutet, dass die Klassen in unserem Datensatz stark gemischt sind. Es ist schwer vorherzusagen, zu welcher Klasse ein neuer Datenpunkt gehören wird. Die "Unordnung" ist groß.

Niedrige Entropie bedeutet, dass die Klassen in unserem Datensatz gut getrennt sind. Die meisten Datenpunkte einer bestimmten Klasse ähneln sich stark. Es ist einfacher vorherzusagen, zu welcher Klasse ein neuer Datenpunkt gehört. Die "Ordnung" ist hoch.

Ein einfaches Beispiel

Stell dir vor, du hast zwei Schüsseln mit Gummibärchen:

• Schüssel A: 8 rote Gummibärchen und 2 grüne Gummibärchen.
• Schüssel B: 5 rote Gummibärchen und 5 grüne Gummibärchen.

Schüssel A hat eine niedrigere Entropie. Es gibt viel mehr rote als grüne Gummibärchen. Wenn du blind ein Gummibärchen ziehst, ist es sehr wahrscheinlich rot. Die "Unsicherheit" ist gering.

Schüssel B hat eine höhere Entropie. Es gibt gleich viele rote und grüne Gummibärchen. Wenn du blind ein Gummibärchen ziehst, ist es schwer vorherzusagen, welche Farbe es haben wird. Die "Unsicherheit" ist groß.

Wie wird Entropie berechnet?

Die Entropie wird mit einer mathematischen Formel berechnet. Es gibt eine genaue Methode, um die "Unordnung" in Zahlen auszudrücken.

P(x_i) ist Formel zur Berechnung der Wahrscheinlichkeit eines Ereignisses. Wobei n_i die Anzahl der Beispiele ist, in denen das Element  x_i auftritt und N die Gesamtzahl der Elemente ist.

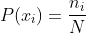
Die Entropie selber berechnet sich mit der Formel H(x). Wobei  P(x_i) die Wahrscheinlichkeit des Ereignisses x_i  ist .

• Hohe Entropie: Wenn die Entropie hoch ist (näher an 1 oder mehr), bedeutet dies, dass viele verschiedene Ergebnisse gleich wahrscheinlich sind. In diesem Fall herrscht große Unsicherheit, und es gibt eine hohe Unordnung im System.
• Niedrige Entropie: Wenn die Entropie niedrig ist (näher an 0), bedeutet dies, dass einige Ergebnisse viel wahrscheinlicher sind als andere. In diesem Fall herrscht geringe Unsicherheit, und es gibt eine höhere Ordnung im System.

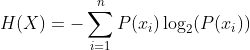
Ein Beispiel

Gegeben ist folgender Datensatz: Kategorie A A B A A B. Entropie lässt sich wie folgt bestimmen:

Die Shannon-Entropie H beträgt ungefähr: H≈0.918

Dies bedeutet, dass die Unsicherheit oder der Informationsgehalt des Ergebnisses in diesem Experiment etwa 0.918 beträgt.

Entropie und maschinellen Lernen

Entropie ist ein wichtiges Konzept, besonders beim Training von Entscheidungsbäumen. Entscheidungsbäume versuchen, die Daten in immer kleinere Gruppen aufzuteilen, bis jede Gruppe möglichst "rein" ist – also nur noch Datenpunkte derselben Klasse enthält.

Bei jedem Schritt überlegt der Entscheidungsbaum, welche Frage (welches Merkmal) die größte Reduktion der Entropie bringt. Das bedeutet, er wählt die Frage, die die "Unordnung" in den resultierenden Gruppen am stärksten verringert und die Daten so besser trennt.

Stell dir vor, du willst herausfinden, ob jemand gerne Pizza mag. Du könntest verschiedene Fragen stellen:

• "Magst du Käse?" (Kann sowohl Pizzafans als auch Nicht-Pizzafans betreffen)
• "Magst du Tomatensauce?" (Ähnlich wie bei Käse)
• "Magst du Pizza?" (Diese Frage trennt die Pizzafans perfekt von den Nicht-Pizzafans!)

Die letzte Frage würde die Entropie am stärksten reduzieren, da die resultierenden Gruppen perfekt "rein" wären (nur Pizzafans oder nur Nicht-Pizzafans).