Algorithmus: Unterschied zwischen den Versionen
Thomas (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Thomas (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 62: | Zeile 62: | ||
Die Anzahl der Schritte, die ein Algorithmus benötigt, wird als die Laufzeit des Algorithmus bezeichnet. Der Begriff Schritt bezieht sich auf das zugrunde gelegte Maschinenmodell. Die Maschine (der Computer) muss in der Lage sein, einen einzelnen Schritt in konstanter Zeit auszuführen. Die Laufzeit hängt im allgemeinen von der Eingabe ab, insbesondere von der Länge der Eingabe, die auch als Problemgröße bezeichnet wird. | Die Anzahl der Schritte, die ein Algorithmus benötigt, wird als die Laufzeit des Algorithmus bezeichnet. Der Begriff Schritt bezieht sich auf das zugrunde gelegte Maschinenmodell. Die Maschine (der Computer) muss in der Lage sein, einen einzelnen Schritt in konstanter Zeit auszuführen. Die Laufzeit hängt im allgemeinen von der Eingabe ab, insbesondere von der Länge der Eingabe, die auch als Problemgröße bezeichnet wird. | ||
Beispiel: Die Laufzeit eines Sortieralgorithmus ist umso größer, je mehr Elemente zu sortieren sind. | Beispiel: Die Laufzeit eines Sortieralgorithmus ist umso größer, je mehr Elemente zu sortieren sind. Soll eine Liste von fünf Zahlen sortiert werden, so ist die Problemgröße n=5. | ||
Soll eine Liste von fünf Zahlen sortiert werden, so ist die Problemgröße n=5. | |||
Bei einer vorsortierten Eingabefolge benötigt der Algorithmus möglicherweise weniger Schritte als bei einer unsortierten Eingabefolge gleicher Länge. Eine vorsortierte Liste stellt das Best Case Szenario dar. Also den günstigsten Fall für das gegebene Problem (hier das Sortieren von Zahlen). Eine sortierte Liste in umgekehrter Reihenfolge stellt das Worst Case Szenario dar. Hier ist der Aufwand am größten die Liste umzusortieren. | Bei einer vorsortierten Eingabefolge benötigt der Algorithmus möglicherweise weniger Schritte als bei einer unsortierten Eingabefolge gleicher Länge. Eine vorsortierte Liste stellt das Best Case Szenario dar. Also den günstigsten Fall für das gegebene Problem (hier das Sortieren von Zahlen). Eine sortierte Liste in umgekehrter Reihenfolge stellt das Worst Case Szenario dar. Hier ist der Aufwand am größten die Liste umzusortieren. | ||
Version vom 29. April 2025, 08:04 Uhr
Algorithmen
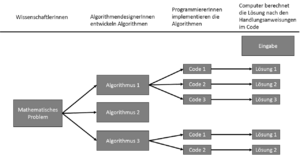
Ein Algorithmus ist in der Informatik ein genau beschriebenes Verfahren zur Lösung eines gegebenen Problems. Ein Programm stellt die Übersetzung eines Algorithmus in eine vom Computer begreifbare und ausführbare Folge von Befehlen dar, an dessen Ende die Lösung eines Problems ausgegeben wird.
Problem --> Algorithmus --> Programm
Somit ist ein Algorithmus universeller als eine konkrete Implementierung.
Einführung
Zwei oft zu bewältigende Probleme in der Informatik sind das Suchen und das Sortieren von Objekten. Allerdings sind Algorithmen für Computer heute so vielfältig wie die Anwendungen, die sie ermöglichen sollen. Vom elektronischen Steuergerät für den Einsatz in KFZ über die Rechtschreib- und Satzbau-Kontrolle in einer Textverarbeitung bis hin zur Analyse von Aktienmärkten finden sich tausende von mehr oder minder tauglich arbeitenden Algorithmen.
Die Lösung komplexer Probleme sollte zuvor designed werden. Hierzu können Algorithmen vor der eigentlichen Programmierung in Ablaufplänen z.B. durch Modelle der UML oder Struktogramme visualisiert werden. Algorithmen werden in der Programmierung durch Kontrollstrukturen oder Rekursion implementiert.
Eigenschaften
Ein Algorithmus in der Informatik ist die Beschreibung eines Verfahrens, um aus gewissen Eingabegrößen bestimmte Ausgabegrößen zu bestimmen. Hierfür müssen folgende Bedingungen erfüllt sein:
Spezifikation
Für Algorithmen werden Schnittstellenspezifikationen benötigt. Sie regeln die Ein- und Ausgabe des Algorithmus. In der Java Programmierung werden Algorithmen mit Methoden realisiert. Die Schnittstelle der Methoden muss in der so genannten Signatur beschrieben werden.
Eingabespezifikation
Es muss genau spezifiziert sein, welche Eingabegrößen erforderlich sind und welche Anforderungen diesen Größen genügen müssen, damit das Verfahren funktioniert. In der Java Programmierung wird die Eingabespezifikation durch so genannte Eingabeparameter definiert.
Ausgabespezifikation
Es muss genau spezifiziert sein, welche Ausgabegrößen (Resultate) mit welchen Eigenschaften bestimmt werden. In der Java Programmierung wird die Ausgabespezifikation durch den so genannten Ausgabeparameter definiert.
Durchführbarkeit
Endliche Beschreibung
Das Verfahren muss mit einem endlichen Text beschrieben werden.
Effektivität
Jeder Schritt des Verfahrens muss tatsächlich durchführbar sein.
Determinismus und Determiniertheit
Wenn der Ablauf zu jedem Zeitpunkt fest vorgeschrieben ist, ist der Algorithmus deterministisch (Determinismus). Für zwei gleiche Eingabegrößen werden jedes Mal exakt die gleichen Rechenschritt in der identischen Reihenfolge durchlaufen. Jeder deterministische Algorithmus ist auch determiniert (Determiniertheit). Der Algorithmus ist determiniert, wenn dieser stets für die gleiche Eingabegröße die gleiche Ausgabegröße liefert! Aber ein determinierter Algorithmus, muss nicht deterministisch sein. Denn determinierte Algorithmen können für gleiche Eingabegrößen jedes Mal auf unterschiedlichen Wegen zum Ziel kommen; liefern aber jedes Mal das gleiche Ergebnis!
Korrektheit
Partielle Korrektheit
Jedes ermittelte Ergebnis genügt der Ausgabespezifikation, sofern die Eingaben der Eingabespezifikation genügen.
Terminierung
Der Algorithmus hält nach endlichen vielen Schritten an, sofern die Eingabe der Eingabespezifikation genügen.
Effizienz
Außerdem sollte der Algorithmus effizient arbeiten. D.h. er sollte nicht zu viel Rechenleistung des Prozessors binden, um die Ausführungszeit nicht unnötig zu verlängern. Dies wird vermieden indem zur Laufzeit eine möglichst minimale Anzahl an Befehlen abgearbeitet werden muss, um das gegebene Problem zu lösen.
Laufzeit
Die Anzahl der Schritte, die ein Algorithmus benötigt, wird als die Laufzeit des Algorithmus bezeichnet. Der Begriff Schritt bezieht sich auf das zugrunde gelegte Maschinenmodell. Die Maschine (der Computer) muss in der Lage sein, einen einzelnen Schritt in konstanter Zeit auszuführen. Die Laufzeit hängt im allgemeinen von der Eingabe ab, insbesondere von der Länge der Eingabe, die auch als Problemgröße bezeichnet wird.
Beispiel: Die Laufzeit eines Sortieralgorithmus ist umso größer, je mehr Elemente zu sortieren sind. Soll eine Liste von fünf Zahlen sortiert werden, so ist die Problemgröße n=5.
Bei einer vorsortierten Eingabefolge benötigt der Algorithmus möglicherweise weniger Schritte als bei einer unsortierten Eingabefolge gleicher Länge. Eine vorsortierte Liste stellt das Best Case Szenario dar. Also den günstigsten Fall für das gegebene Problem (hier das Sortieren von Zahlen). Eine sortierte Liste in umgekehrter Reihenfolge stellt das Worst Case Szenario dar. Hier ist der Aufwand am größten die Liste umzusortieren.
Um den Algorithmus unabhängig von der konkreten Eingabe bewerten zu können, betrachtet man die Zeitkomplexität in der so genannten Laufzeitanalyse.
Beispiel
Das folgende Beispiel zeigt einen Algorithmus in der Programmiersprache Java der z.B. Bücher in einem Regal sortiert:
// Sortieren durch Vertauschen unmittelbarer Nachbarn
// beim ersten Durchgang "perlt" die größte Zahl nach hinten, so dass
// spätere Durtchgänge immer ein Element früher enden können und so
// der sortierte Teil von hinten nach vorne wächst
int durchgang, stelle;
for (durchgang=1; durchgang<reihung.length; durchgang++){
// Es werden alle zu durchsuchenden Elemente Schritt für Schritt durchlaufen
for (stelle=0; stelle<reihung.length-durchgang; stelle++){
// Durchgänge beginnen immer bei 0, enden aber immer früher
if (reihung[stelle] > reihung[stelle+1]){
// Nachbarn in falscher Reihenfolge werden vertauscht
tausche (stelle, stelle+1);
}
}
}