Quadratische Funktion: Unterschied zwischen den Versionen
| Zeile 149: | Zeile 149: | ||
<math>x^2+3x+2,5=0</math> | <math>x^2+3x+2,5=0</math> | ||
damit wir die p-q-Formel anwenden können. Es gilt p=3 und q=2,5. Diese Werte können wir in die p-q-Formel einsetzen: | |||
<math>x=-\frac{3}{2}\pm\sqrt{\left(\frac{3}{2}\right)^2-2,5}=-1,5\pm\sqrt{-0,25}</math> | |||
Aus negativen Zahlen können wir keine Wurzel ziehen, daher existiert keine Schnittstelle. Das lässt sich auch im Koordinatensystem erkennen. | Aus negativen Zahlen können wir keine Wurzel ziehen, daher existiert keine Schnittstelle. Das lässt sich auch im Koordinatensystem erkennen. | ||
damit wir die p-q-Formel anwenden können. Es gilt p=3 und q=2, | |||
x=-\frac{3}{2}\pm\sqrt{\left(\frac{3}{2}\right)^2-2,5}=-1,5\pm\sqrt{-0, | ====Parabel und Gerade haben genau einen Schnittpunkt==== | ||
[[Datei:QuadratischeFunktionenBeispielEinSchnitt.png|mini|Graphen der Funktionen <math>{f\left(x\right)=2x}^2+4x+4</math> und <math>g\left(x\right)=-2x-0,5</math> mit genau einem Schnittpunkt]] | |||
Wir betrachten <math>{f\left(x\right)=2x}^2+4x+4</math> und <math>g\left(x\right)=-2x-0,5</math>. Wir setzen die Funktionen gleich und rechnen | |||
<math>{2x}^2+4x+4=-2x-0,5\ |+0,5</math> | |||
<math>{2x}^2+4x+4,5=-2x\ |+2x</math> | |||
<math>{2x}^2+6x+4,5=0\ |\div2</math> | |||
<math>x^2+3x+2,25=0</math> | |||
damit wir die p-q-Formel anwenden können. Es gilt <math>p=3</math> und <math>q=2,25</math>. Diese Werte können wir in die p-q-Formel einsetzen: | |||
<math>x=-\frac{3}{2}\pm\sqrt{\left(\frac{3}{2}\right)^2-2,25}=-1,5\pm\sqrt0=-1,5</math> | |||
Den y-Wert berechnen wir durch <math>g\left(-1,5\right)=-2\cdot\left(-1,5\right)-0,5=2,5</math>. Der Schnittpunkt ist damit <math>A(-1,5|2,5)</math>. | |||
====Parabel und Gerade haben zwei Schnittpunkte==== | |||
[[Datei:QuadratischeFunktionenBeispielZweiSchnitt.png|mini|Graphen der Funktionen <math>{f\left(x\right)=2x}^2+4x+4</math> und <math>g\left(x\right)=-2x</math> mit zwei Schnittpunkten]] | |||
Wir betrachten <math>{f\left(x\right)=2x}^2+4x+4</math> und <math>g\left(x\right)=-2x</math>. Wir setzen die Funktionen gleich und rechnen | |||
<math>{2x}^2+4x+4=-2x\ |+2x</math> | |||
<math>{2x}^2+6x+4=0\ |\div2</math> | |||
<math>x^2+3x+2=0</math> | |||
damit wir die p-q-Formel anwenden können. Es gilt <math>p=3</math> und <math>q=2</math>. Diese Werte können wir in die p-q-Formel einsetzen: | |||
<math>x_1=-\frac{3}{2}+\sqrt{\left(\frac{3}{2}\right)^2-2}=-1,5+\sqrt{0,25}=-1</math> | |||
und | |||
<math>x_2=-\frac{3}{2}-\sqrt{\left(\frac{3}{2}\right)^2-2}=-1,5-\sqrt{0,25}=-2</math> | |||
Die y-Werte berechnen wir durch <math>g\left(-1\right)=-2\cdot\left(-1\right)=2</math> und <math>g\left(-2\right)=-2\cdot\left(-2\right)=4</math>. Die Schnittpunkte sind damit <math>A(-1|2)</math> und <math>B(-2|4)</math>. | |||
====Zwei Parabeln ohne Schnittpunkt==== | |||
[[Datei:QuadratischeFunktionenBeispielParaOhneSchnitt.png|mini|Graphen der Funktionen <math>{f\left(x\right)=2x}^2+4x+4</math> und <math>{h\left(x\right)=-3x}^2-2x+1</math> ohne Schnittpunkt]] | |||
Betrachten wir zwei Parabeln, treten die gleichen drei Fälle wie oben auf. Wir betrachten hier nur den Fall, bei dem die Parabeln keine Schnittpunkte haben. | |||
Wir betrachten <math>{f\left(x\right)=2x}^2+4x+4</math> und <math>{h\left(x\right)=-3x}^2-2x+1</math>. Gleichsetzen der Funktionen liefert | |||
<math>{{-3x}^2-2x+1=2x}^2+4x+4\ |-2x²</math> | |||
<math>{-5x}^2-2x+1=4x+4\ |-4x</math> | |||
<math>{-5x}^2-6x+1=4\ |-4</math> | |||
<math>{-5x}^2-6x-3=0\ |\div(-5)</math> | |||
<math>x^2+1,2x+0,6=0</math> | |||
Es gilt <math>p=1,2</math> und <math>q=0,6</math>. | |||
Diese Werte können wir einsetzen: | |||
<math>x=-\frac{1,2}{2}\pm\sqrt{\left(\frac{1,2}{2}\right)^2-0,6}=-0,6\pm\sqrt{-0,24}</math> | |||
Der Wert unter der Wurzel ist negativ und damit existiert kein Schnittpunkt. | |||
Version vom 13. Januar 2024, 09:58 Uhr
Lineare Funktionen sind Funktionen der Form [math]\displaystyle{ f(x)=ax^2+bx+c }[/math]. Der Graph einer linearen Funktion ist eine Gerade. Anwendungen finden quadratische Funktionen in der Marktanalyse.
Betrag einer Zahl
Der Betrag einer reellen Zahl a misst den Abstand zu 0 und wird mit [math]\displaystyle{ |a| }[/math] abgekürzt. Es gilt [math]\displaystyle{ a=\left\{\begin{array}{ll} a, & a \geq 0 \\ -a, & a\lt 0\end{array}\right. . }[/math] Wir verwenden den Betrag bei der Definition einer quadratischen Funktion.
Beispiel
Es gilt [math]\displaystyle{ \left|1\right|=1, \left|-2\right|=2, \left|0\right|=0, \left|-1\right|=1, \left|3\right|=3 }[/math].
Definition
Eine Funktion der Form [math]\displaystyle{ f\left(x\right)=ax^2+bx+c }[/math] mit [math]\displaystyle{ a\neq0 }[/math] heißt quadratische Funktion in Normalform, ihr Graph heißt Parabel. [math]\displaystyle{ a }[/math] heißt Streckungsfaktor, wenn [math]\displaystyle{ |a|\gt 1 }[/math] und Stauchungsfaktor, wenn [math]\displaystyle{ |a|\lt 1 }[/math]. Für [math]\displaystyle{ a\gt 0 }[/math] ist die Parabel nach oben geöffnet, für [math]\displaystyle{ a\lt 0 }[/math] ist die Parabel nach unten geöffnet. Der tiefste bzw. höchster Punkt heißt Scheitelpunkt oder Scheitel S. Der Graph von [math]\displaystyle{ f\left(x\right)=x^2 }[/math] heißt Normalparabel.
Beispiele für quadratische Funktionen
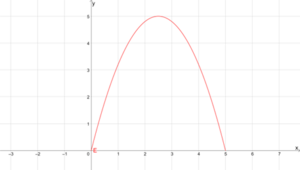
Der Graph der Funktion [math]\displaystyle{ E(x)=-0,8x^2+4x }[/math] mit dem Definitionsbereich [math]\displaystyle{ \mathbb{D}_E=[0;5] }[/math] ist auf der rechten Seite dargestellt. Der Scheitelpunkt ist [math]\displaystyle{ S(2,5|5) }[/math]. Die Normalparabel wurde um den Faktor [math]\displaystyle{ -0,8 }[/math] gestaucht und ist nach unten geöffnet. Der Schnittpunkt mit der y-Achse ist [math]\displaystyle{ (0|0) }[/math].
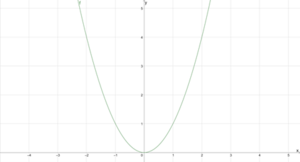
Der nächste Graph ist die Normalparabel zur Funktion [math]\displaystyle{ f(x)=x^2 }[/math] mit dem Scheitelpunkt [math]\displaystyle{ S(0|0) }[/math] und wurde daher weder gestaucht, noch gestreckt, da [math]\displaystyle{ a=1 }[/math] ist. Der Schnittpunkt mit der y-Achse ist [math]\displaystyle{ (0/0) }[/math].
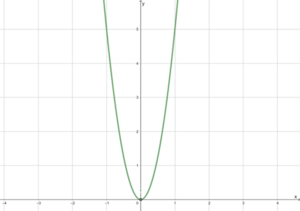
Der letzte Graph ist hat die Funktionsvorschrift [math]\displaystyle{ f(x)=5x^2 }[/math] mit dem Scheitelpunkt [math]\displaystyle{ S(0|0) }[/math] und wurde daher um 5 Einheiten gestreckt, da [math]\displaystyle{ a=5 }[/math] ist. Der Schnittpunkt mit der y-Achse ist [math]\displaystyle{ (0/0) }[/math].
Nullstellen
Die Nullstellen einer quadratischen Funktion [math]\displaystyle{ {f\left(x\right)=x}^2+px+q }[/math] werden durch Auflösen der Gleichung [math]\displaystyle{ x^2+px+q=0 }[/math] nach [math]\displaystyle{ x }[/math] ausgerechnet. Für eine Nachfragefunktion wird die positive Nullstelle auch Sättigungsmenge genannt. Die Lösung der Gleichung wird mit der p-q-Formel berechnet: [math]\displaystyle{ x=-\frac{p}{2}\pm\sqrt{\left(\frac{p}{2}\right)^2-q} }[/math]
Es können keine, eine oder zwei Lösungen existieren.
Beispiel pq-Formel anwenden
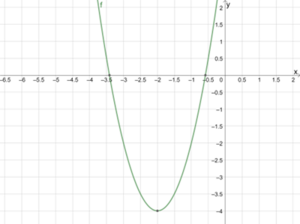
Wir betrachten [math]\displaystyle{ {f\left(x\right)=2x}^2+8x+4 }[/math]. Wir rechnen
[math]\displaystyle{ {2x}^2+8x+4=0\ |\ \div2 }[/math]
[math]\displaystyle{ x^2+4x+2=0\ }[/math]
damit wir die p-q-Formel anwenden können. Es gilt [math]\displaystyle{ p=4 }[/math] und [math]\displaystyle{ q=2 }[/math]. Diese Werte können wir einsetzen: [math]\displaystyle{ x_1=-\frac{4}{2}+\sqrt{\left(\frac{4}{2}\right)^2-2}=-2-\sqrt2\approx-3,41 }[/math] und [math]\displaystyle{ x_2=-\frac{4}{2}+\sqrt{\left(\frac{4}{2}\right)^2-2}=-2+\sqrt2\approx-0,59 }[/math]
Also hat f die Nullstellen [math]\displaystyle{ x_1\approx-3,41 }[/math] und [math]\displaystyle{ x_2\approx-0,59 }[/math]. Das sind die x-Werte, bei denen der Graph die x-Achse schneidet.
Beispiel Nullstellen ohne pq-Formel berechnen
Einige Nullstellen bzw. Lösungen von quadratischen Gleichungen können auch ohne p-q-Formel bestimmt werden:
Direktes Auflösen einer quadratischen Gleichung nach x:
[math]\displaystyle{ 3\left(x-5\right)^2=27\ |\ \div3 }[/math]
[math]\displaystyle{ \left(x-5\right)^2=9\ |\ \sqrt{~} }[/math]
[math]\displaystyle{ x-5=9\ \vee x-5=-9\ |+5 }[/math]
[math]\displaystyle{ x=14\ \vee x=-4 }[/math]
Produkt von Nullstellen:
[math]\displaystyle{ \left(x-8\right)\left(x+3\right)=0 }[/math]
[math]\displaystyle{ x-8=0\ \vee x-3=0 }[/math]
[math]\displaystyle{ x=8\ \vee x=3 }[/math]
Direktes Auflösen nach x:
[math]\displaystyle{ 7x^2-343=0\ |\ \div7 }[/math]
[math]\displaystyle{ x^2-49=0\ |+49 }[/math]
[math]\displaystyle{ x^2=49\ \ |\ \sqrt{~} }[/math]
[math]\displaystyle{ x=7\ \vee x=-7\ }[/math]
Herleitung p-q-Formel (nur zur Vertiefung)
Um die Nullstellen einer beliebigen quadratischen Funktion [math]\displaystyle{ f\left(x\right)=ax^2+bx+c }[/math] zu bestimmen, rechnet man:
[math]\displaystyle{ ax^2+bx+c=0 }[/math]
[math]\displaystyle{ a{(x}^2+\frac{b}{a}x)+c=0 }[/math]
[math]\displaystyle{ a{(x}^2+\frac{b}{a}x)+c=0 }[/math]
[math]\displaystyle{ a{(x}^2+\frac{b}{a}x+\left(\frac{b}{2a}\right)^2-\left(\frac{b}{2a}\right)^2)+c=0 }[/math]
[math]\displaystyle{ a{(x+\frac{b}{2a})}^2-\left(\frac{b}{2}\right)^2+c=0 }[/math]
[math]\displaystyle{ a\left(x+\frac{b}{2a}\right)=\pm\sqrt{\left(\frac{b}{2}\right)^2-c} }[/math]
[math]\displaystyle{ x=-\frac{b}{2a}\pm\sqrt{\frac{1}{a}{(\left(\frac{b}{2}\right)}^2-c)} }[/math]
Gilt [math]\displaystyle{ a=1 }[/math], so erhält man:
[math]\displaystyle{ x=-\frac{b}{2}\pm\sqrt{{(\left(\frac{b}{2}\right)}^2-c)} }[/math]
Nullstellenform
Eine Funktion der Form [math]\displaystyle{ f\left(x\right)=a(x-x_1)(x-x_2) }[/math] heißt quadratische Funktion in Nullstellenform. Die Nullstellen sind [math]\displaystyle{ x_1 }[/math] und [math]\displaystyle{ x_2 }[/math].
Beispiel mit Nullstellen [math]\displaystyle{ x_1=3 }[/math] und [math]\displaystyle{ x_2=-4 }[/math]
[math]\displaystyle{ x_1=3 }[/math] und [math]\displaystyle{ x_2=-4 }[/math] sind Nullstellen von [math]\displaystyle{ f }[/math] mit [math]\displaystyle{ a=1 }[/math], dann ist [math]\displaystyle{ f\left(x\right)=1 \cdot (x-3)\cdot (x+4) }[/math] in Nullstellenform.
Beispiel mit Nullstellen [math]\displaystyle{ x_1=2 }[/math] und [math]\displaystyle{ x_2=6 }[/math]
[math]\displaystyle{ x_1=2 }[/math] und [math]\displaystyle{ x_2=6 }[/math] sind Nullstellen von [math]\displaystyle{ g }[/math] mit [math]\displaystyle{ a=-3 }[/math], dann ist [math]\displaystyle{ g\left(x\right)=(-3)\cdot (x-2) \cdot (x-6) }[/math] in Nullstellenform.
Scheitelpunktform
Eine Funktion der Form [math]\displaystyle{ f\left(x\right)=a({x-e)}^2+f }[/math] mit [math]\displaystyle{ a\neq0 }[/math] heißt quadratische Funktion in Scheitelpunktform. Der Scheitelpunkt ist [math]\displaystyle{ S(e|f) }[/math]. Der Faktor [math]\displaystyle{ a }[/math] ist in der Scheitelpunktform und der Normalform der Gleiche.
Beispiel
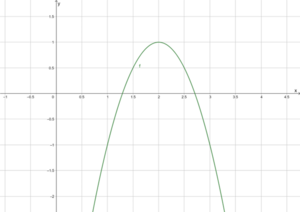
Wir betrachten die Funktion [math]\displaystyle{ f\left(x\right)=-2({x-2)}^2+1 }[/math]. Der Scheitelpunkt ist dann [math]\displaystyle{ S(2|1) }[/math]. Man kann die rechte Seite der Funktion weiter auflösen, um von der Scheitelpunktform zur Normalform zu kommen:
[math]\displaystyle{ f\left(x\right)=-2({x-2)}^2+1 }[/math]
[math]\displaystyle{ f\left(x\right)=-2(x^2-4x+4)+1 }[/math]
[math]\displaystyle{ f\left(x\right)=-2x^2+8x-8+1 }[/math]
[math]\displaystyle{ f\left(x\right)=-2x^2+8x-7 }[/math]
Der Graph der Funktion ist auf der rechten Seite aufgelistet. Der Schnittpunkt mit der y-Achse ist [math]\displaystyle{ (0|-7) }[/math].
Schnittpunkte von Parabeln und Geraden berechnen
Sind eine lineare Funktion [math]\displaystyle{ y=mx+b }[/math] und eine quadratische Funktion [math]\displaystyle{ y=ax^2+bx+c }[/math] gegeben, kann die Schnittstelle durch Gleichsetzen, [math]\displaystyle{ ax^2+bx+c=mx+b\ }[/math], und Umformen nach x errechnet werden. Wurde so umgeformt, dass auf einer Seite eine 0 steht, kann die p-q-Formel angwendet werden und wir erhalten die Schnittstellen. Anschließend werden die dazugehörigen y-Werte durch Einsetzen der x-Werte in die quadratische oder lineare Funktion berechnet. Für zwei quadratische Funktionen oder lineare Funktionen ist das Vorgehen analog.
Beispiele Schnittpunkte von Parabel und Gerade
Wir betrachten im Folgenden die drei Fälle für Schnittpunkte von Parabel und Gerade.
Parabel und Gerade haben keinen Schnittpunkt
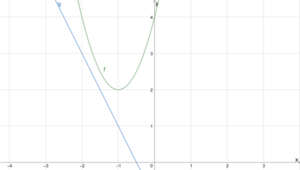
Wir betrachten [math]\displaystyle{ {f\left(x\right)=2x}^2+4x+4 }[/math] und [math]\displaystyle{ g\left(x\right)=-2x-1 }[/math]. Wir setzen die Funktionen gleich und rechnen
[math]\displaystyle{ {2x}^2+4x+4=-2x-1\ |+1 }[/math]
[math]\displaystyle{ {2x}^2+4x+5=-2x\ |+2x }[/math]
[math]\displaystyle{ {2x}^2+6x+5=0\ |\div2 }[/math]
[math]\displaystyle{ x^2+3x+2,5=0 }[/math]
damit wir die p-q-Formel anwenden können. Es gilt p=3 und q=2,5. Diese Werte können wir in die p-q-Formel einsetzen: [math]\displaystyle{ x=-\frac{3}{2}\pm\sqrt{\left(\frac{3}{2}\right)^2-2,5}=-1,5\pm\sqrt{-0,25} }[/math]
Aus negativen Zahlen können wir keine Wurzel ziehen, daher existiert keine Schnittstelle. Das lässt sich auch im Koordinatensystem erkennen.
Parabel und Gerade haben genau einen Schnittpunkt
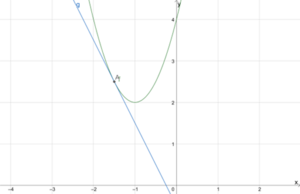
Wir betrachten [math]\displaystyle{ {f\left(x\right)=2x}^2+4x+4 }[/math] und [math]\displaystyle{ g\left(x\right)=-2x-0,5 }[/math]. Wir setzen die Funktionen gleich und rechnen
[math]\displaystyle{ {2x}^2+4x+4=-2x-0,5\ |+0,5 }[/math]
[math]\displaystyle{ {2x}^2+4x+4,5=-2x\ |+2x }[/math]
[math]\displaystyle{ {2x}^2+6x+4,5=0\ |\div2 }[/math]
[math]\displaystyle{ x^2+3x+2,25=0 }[/math]
damit wir die p-q-Formel anwenden können. Es gilt [math]\displaystyle{ p=3 }[/math] und [math]\displaystyle{ q=2,25 }[/math]. Diese Werte können wir in die p-q-Formel einsetzen: [math]\displaystyle{ x=-\frac{3}{2}\pm\sqrt{\left(\frac{3}{2}\right)^2-2,25}=-1,5\pm\sqrt0=-1,5 }[/math]
Den y-Wert berechnen wir durch [math]\displaystyle{ g\left(-1,5\right)=-2\cdot\left(-1,5\right)-0,5=2,5 }[/math]. Der Schnittpunkt ist damit [math]\displaystyle{ A(-1,5|2,5) }[/math].
Parabel und Gerade haben zwei Schnittpunkte
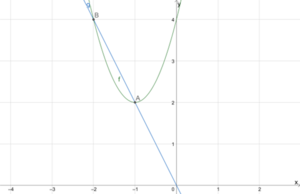
Wir betrachten [math]\displaystyle{ {f\left(x\right)=2x}^2+4x+4 }[/math] und [math]\displaystyle{ g\left(x\right)=-2x }[/math]. Wir setzen die Funktionen gleich und rechnen
[math]\displaystyle{ {2x}^2+4x+4=-2x\ |+2x }[/math]
[math]\displaystyle{ {2x}^2+6x+4=0\ |\div2 }[/math]
[math]\displaystyle{ x^2+3x+2=0 }[/math]
damit wir die p-q-Formel anwenden können. Es gilt [math]\displaystyle{ p=3 }[/math] und [math]\displaystyle{ q=2 }[/math]. Diese Werte können wir in die p-q-Formel einsetzen:
[math]\displaystyle{ x_1=-\frac{3}{2}+\sqrt{\left(\frac{3}{2}\right)^2-2}=-1,5+\sqrt{0,25}=-1 }[/math]
und
[math]\displaystyle{ x_2=-\frac{3}{2}-\sqrt{\left(\frac{3}{2}\right)^2-2}=-1,5-\sqrt{0,25}=-2 }[/math]
Die y-Werte berechnen wir durch [math]\displaystyle{ g\left(-1\right)=-2\cdot\left(-1\right)=2 }[/math] und [math]\displaystyle{ g\left(-2\right)=-2\cdot\left(-2\right)=4 }[/math]. Die Schnittpunkte sind damit [math]\displaystyle{ A(-1|2) }[/math] und [math]\displaystyle{ B(-2|4) }[/math].
Zwei Parabeln ohne Schnittpunkt
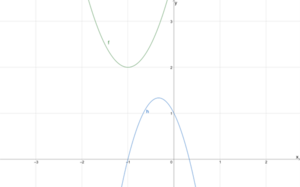
Betrachten wir zwei Parabeln, treten die gleichen drei Fälle wie oben auf. Wir betrachten hier nur den Fall, bei dem die Parabeln keine Schnittpunkte haben.
Wir betrachten [math]\displaystyle{ {f\left(x\right)=2x}^2+4x+4 }[/math] und [math]\displaystyle{ {h\left(x\right)=-3x}^2-2x+1 }[/math]. Gleichsetzen der Funktionen liefert
[math]\displaystyle{ {{-3x}^2-2x+1=2x}^2+4x+4\ |-2x² }[/math]
[math]\displaystyle{ {-5x}^2-2x+1=4x+4\ |-4x }[/math]
[math]\displaystyle{ {-5x}^2-6x+1=4\ |-4 }[/math]
[math]\displaystyle{ {-5x}^2-6x-3=0\ |\div(-5) }[/math]
[math]\displaystyle{ x^2+1,2x+0,6=0 }[/math]
Es gilt [math]\displaystyle{ p=1,2 }[/math] und [math]\displaystyle{ q=0,6 }[/math].
Diese Werte können wir einsetzen:
[math]\displaystyle{ x=-\frac{1,2}{2}\pm\sqrt{\left(\frac{1,2}{2}\right)^2-0,6}=-0,6\pm\sqrt{-0,24} }[/math]
Der Wert unter der Wurzel ist negativ und damit existiert kein Schnittpunkt.