Quadratische Funktion: Unterschied zwischen den Versionen
| Zeile 36: | Zeile 36: | ||
Eine Funktion der Form <math>f\left(x\right)=a({x-e)}^2+f</math> mit <math>a\neq0</math> heißt quadratische Funktion in '''Scheitelpunktform'''. Der Scheitelpunkt ist <math>S(e|f)</math>. Der Faktor <math>a</math> ist in der Scheitelpunktform und der Normalform der Gleiche. | Eine Funktion der Form <math>f\left(x\right)=a({x-e)}^2+f</math> mit <math>a\neq0</math> heißt quadratische Funktion in '''Scheitelpunktform'''. Der Scheitelpunkt ist <math>S(e|f)</math>. Der Faktor <math>a</math> ist in der Scheitelpunktform und der Normalform der Gleiche. | ||
[[Datei:QuadratischeFunktionenBeispielQuadFktScheitelpf.png|mini|Graph der Funktion <math>f\left(x\right)=-2({x-2)}^2+1</math>]] | |||
===Beispiel=== | ===Beispiel=== | ||
Wir betrachten die Funktion <math>f\left(x\right)=-2({x-2)}^2+1</math>. Der Scheitelpunkt ist dann <math>S(2|1)</math>. Man kann die rechte Seite der Funktion weiter auflösen, um von der Scheitelpunktform zur Normalform zu kommen: | Wir betrachten die Funktion <math>f\left(x\right)=-2({x-2)}^2+1</math>. Der Scheitelpunkt ist dann <math>S(2|1)</math>. Man kann die rechte Seite der Funktion weiter auflösen, um von der Scheitelpunktform zur Normalform zu kommen: | ||
| Zeile 46: | Zeile 47: | ||
<math>f\left(x\right)=-2x^2+8x-7</math> | <math>f\left(x\right)=-2x^2+8x-7</math> | ||
Der Graph der Funktion ist auf der rechten Seite aufgelistet. Der Schnittpunkt mit der y-Achse ist <math>(0|-7)</math>. | |||
Version vom 13. Januar 2024, 08:56 Uhr
Lineare Funktionen sind Funktionen der Form [math]\displaystyle{ f(x)=ax^2+bx+c }[/math]. Der Graph einer linearen Funktion ist eine Gerade. Anwendungen finden quadratische Funktionen in der Marktanalyse.
Betrag einer Zahl
Der Betrag einer reellen Zahl a misst den Abstand zu 0 und wird mit [math]\displaystyle{ |a| }[/math] abgekürzt. Es gilt [math]\displaystyle{ a=\left\{\begin{array}{ll} a, & a \geq 0 \\ -a, & a\lt 0\end{array}\right. . }[/math] Wir verwenden den Betrag bei der Definition einer quadratischen Funktion.
Beispiel
Es gilt [math]\displaystyle{ \left|1\right|=1, \left|-2\right|=2, \left|0\right|=0, \left|-1\right|=1, \left|3\right|=3 }[/math].
Definition
Eine Funktion der Form [math]\displaystyle{ f\left(x\right)=ax^2+bx+c }[/math] mit [math]\displaystyle{ a\neq0 }[/math] heißt quadratische Funktion in Normalform, ihr Graph heißt Parabel. [math]\displaystyle{ a }[/math] heißt Streckungsfaktor, wenn [math]\displaystyle{ |a|\gt 1 }[/math] und Stauchungsfaktor, wenn [math]\displaystyle{ |a|\lt 1 }[/math]. Für [math]\displaystyle{ a\gt 0 }[/math] ist die Parabel nach oben geöffnet, für [math]\displaystyle{ a\lt 0 }[/math] ist die Parabel nach unten geöffnet. Der tiefste bzw. höchster Punkt heißt Scheitelpunkt oder Scheitel S. Der Graph von [math]\displaystyle{ f\left(x\right)=x^2 }[/math] heißt Normalparabel.
Beispiele für quadratische Funktionen
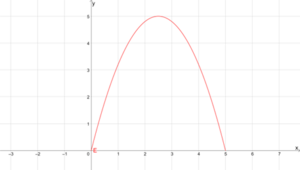
Der Graph der Funktion [math]\displaystyle{ E(x)=-0,8x^2+4x }[/math] mit dem Definitionsbereich [math]\displaystyle{ \mathbb{D}_E=[0;5] }[/math] ist auf der rechten Seite dargestellt. Der Scheitelpunkt ist [math]\displaystyle{ S(2,5|5) }[/math]. Die Normalparabel wurde um den Faktor [math]\displaystyle{ -0,8 }[/math] gestaucht und ist nach unten geöffnet. Der Schnittpunkt mit der y-Achse ist [math]\displaystyle{ (0|0) }[/math].
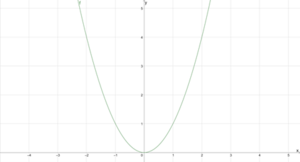
Der nächste Graph ist die Normalparabel zur Funktion [math]\displaystyle{ f(x)=x^2 }[/math] mit dem Scheitelpunkt [math]\displaystyle{ S(0|0) }[/math] und wurde daher weder gestaucht, noch gestreckt, da [math]\displaystyle{ a=1 }[/math] ist. Der Schnittpunkt mit der y-Achse ist [math]\displaystyle{ (0/0) }[/math].
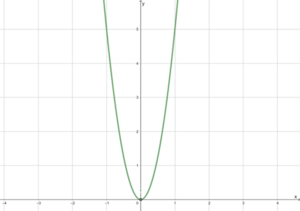
Der letzte Graph ist hat die Funktionsvorschrift [math]\displaystyle{ f(x)=5x^2 }[/math] mit dem Scheitelpunkt [math]\displaystyle{ S(0|0) }[/math] und wurde daher um 5 Einheiten gestreckt, da [math]\displaystyle{ a=5 }[/math] ist. Der Schnittpunkt mit der y-Achse ist [math]\displaystyle{ (0/0) }[/math].
Nullstellenform
Eine Funktion der Form [math]\displaystyle{ f\left(x\right)=a(x-x_1)(x-x_2) }[/math] heißt quadratische Funktion in Nullstellenform. Die Nullstellen sind [math]\displaystyle{ x_1 }[/math] und [math]\displaystyle{ x_2 }[/math].
Beispiel mit Nullstellen [math]\displaystyle{ x_1=3 }[/math] und [math]\displaystyle{ x_2=-4 }[/math]
[math]\displaystyle{ x_1=3 }[/math] und [math]\displaystyle{ x_2=-4 }[/math] sind Nullstellen von [math]\displaystyle{ f }[/math] mit [math]\displaystyle{ a=1 }[/math], dann ist [math]\displaystyle{ f\left(x\right)=1 \cdot (x-3)\cdot (x+4) }[/math] in Nullstellenform.
Beispiel mit Nullstellen [math]\displaystyle{ x_1=2 }[/math] und [math]\displaystyle{ x_2=6 }[/math]
[math]\displaystyle{ x_1=2 }[/math] und [math]\displaystyle{ x_2=6 }[/math] sind Nullstellen von [math]\displaystyle{ g }[/math] mit [math]\displaystyle{ a=-3 }[/math], dann ist [math]\displaystyle{ g\left(x\right)=(-3)\cdot (x-2) \cdot (x-6) }[/math] in Nullstellenform.
Scheitelpunktform
Eine Funktion der Form [math]\displaystyle{ f\left(x\right)=a({x-e)}^2+f }[/math] mit [math]\displaystyle{ a\neq0 }[/math] heißt quadratische Funktion in Scheitelpunktform. Der Scheitelpunkt ist [math]\displaystyle{ S(e|f) }[/math]. Der Faktor [math]\displaystyle{ a }[/math] ist in der Scheitelpunktform und der Normalform der Gleiche.
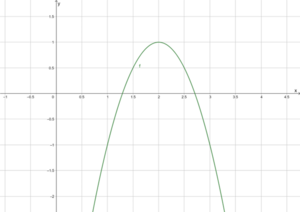
Beispiel
Wir betrachten die Funktion [math]\displaystyle{ f\left(x\right)=-2({x-2)}^2+1 }[/math]. Der Scheitelpunkt ist dann [math]\displaystyle{ S(2|1) }[/math]. Man kann die rechte Seite der Funktion weiter auflösen, um von der Scheitelpunktform zur Normalform zu kommen:
[math]\displaystyle{ f\left(x\right)=-2({x-2)}^2+1 }[/math]
[math]\displaystyle{ f\left(x\right)=-2(x^2-4x+4)+1 }[/math]
[math]\displaystyle{ f\left(x\right)=-2x^2+8x-8+1 }[/math]
[math]\displaystyle{ f\left(x\right)=-2x^2+8x-7 }[/math]
Der Graph der Funktion ist auf der rechten Seite aufgelistet. Der Schnittpunkt mit der y-Achse ist [math]\displaystyle{ (0|-7) }[/math].