Quadratische Funktion: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| Zeile 25: | Zeile 25: | ||
<html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/64UjI-hUQIU?si=2PmAymgjsY8d9YsQ" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe><iframe width="280" height="157.5" src="https://www.youtube.com/embed/_1k7_zaN4q4?si=tNfzoDlVV4Q2tRmx" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | <html><iframe width="280" height="157.5" src="https://www.youtube.com/embed/64UjI-hUQIU?si=2PmAymgjsY8d9YsQ" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe><iframe width="280" height="157.5" src="https://www.youtube.com/embed/_1k7_zaN4q4?si=tNfzoDlVV4Q2tRmx" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe></html> | ||
==Nullstellen== | |||
Die '''Nullstellen''' einer quadratischen Funktion <math>{f\left(x\right)=x}^2+px+q</math> werden durch Auflösen der Gleichung <math>x^2+px+q=0</math> nach <math>x</math> ausgerechnet. Für eine Nachfragefunktion wird die positive Nullstelle auch '''Sättigungsmenge''' genannt. Die Lösung der Gleichung wird mit der '''p-q-Formel''' berechnet: <math>x_{1,2}=-\frac{p}{2}\pm\sqrt{\left(\frac{p}{2}\right)^2-q}</math> | |||
===Beispiel pq-Formel=== | |||
[[Datei:QuadratischeFunktionenBeispielQuadFktNST.png|mini|Graph der Funktion <math>f(x)=2x^2+8x+4</math> mit Nullstellen]] | |||
Wir betrachten <math>{f\left(x\right)=2x}^2+8x+4</math>. Wir rechnen | |||
<math>{2x}^2+8x+4=0\ |\ \div2</math> | |||
<math>x^2+4x+2=0\ </math> | |||
damit wir die p-q-Formel anwenden können. Es gilt <math>p=4</math> und <math>q=2</math>. Diese Werte können wir einsetzen: | |||
<math>x_1=-\frac{4}{2}+\sqrt{\left(\frac{4}{2}\right)^2-2}=-2-\sqrt2\approx-3,41</math> | |||
und | |||
<math>x_2=-\frac{4}{2}+\sqrt{\left(\frac{4}{2}\right)^2-2}=-2+\sqrt2\approx-0,59</math> | |||
Also hat f die Nullstellen <math>x_1\approx-3,41</math> und <math>x_2\approx-0,59</math>. Das sind die x-Werte, bei denen der Graph die x-Achse schneidet: | |||
===Nullstellen ohne pq-Formel berechnen=== | |||
Einige Nullstellen bzw. Lösungen von quadratischen Gleichungen können auch ohne p-q-Formel bestimmt werden: | |||
Direktes Auflösen einer quadratischen Gleichung nach x: | |||
<math>3\left(x-5\right)^2=27\ |\ \div3</math> | |||
<math>\left(x-5\right)^2=9\ |\ \sqrt{~}</math> | |||
<math>x-5=9\ \vee x-5=-9\ |+5</math> | |||
<math>x=14\ \vee x=-4</math> | |||
Produkt von Nullstellen: | |||
<math>\left(x-8\right)\left(x+3\right)=0</math> | |||
<math>x-8=0\ \vee x-3=0</math> | |||
<math>x=8\ \vee x=3</math> | |||
Direktes Auflösen nach x: | |||
<math>7x^2-343=0\ |\ \div7</math> | |||
<math>x^2-49=0\ |+49</math> | |||
<math>x^2=49\ \ |\ \sqrt{~}</math> | |||
<math>x=7\ \vee x=-7\</math> | |||
==Nullstellenform== | ==Nullstellenform== | ||
| Zeile 52: | Zeile 101: | ||
Der Graph der Funktion ist auf der rechten Seite aufgelistet. Der Schnittpunkt mit der y-Achse ist <math>(0|-7)</math>. | Der Graph der Funktion ist auf der rechten Seite aufgelistet. Der Schnittpunkt mit der y-Achse ist <math>(0|-7)</math>. | ||
==Schnittpunkte von Parabeln== | ==Schnittpunkte von Parabeln== | ||
Version vom 13. Januar 2024, 09:16 Uhr
Lineare Funktionen sind Funktionen der Form [math]\displaystyle{ f(x)=ax^2+bx+c }[/math]. Der Graph einer linearen Funktion ist eine Gerade. Anwendungen finden quadratische Funktionen in der Marktanalyse.
Betrag einer Zahl
Der Betrag einer reellen Zahl a misst den Abstand zu 0 und wird mit [math]\displaystyle{ |a| }[/math] abgekürzt. Es gilt [math]\displaystyle{ a=\left\{\begin{array}{ll} a, & a \geq 0 \\ -a, & a\lt 0\end{array}\right. . }[/math] Wir verwenden den Betrag bei der Definition einer quadratischen Funktion.
Beispiel
Es gilt [math]\displaystyle{ \left|1\right|=1, \left|-2\right|=2, \left|0\right|=0, \left|-1\right|=1, \left|3\right|=3 }[/math].
Definition
Eine Funktion der Form [math]\displaystyle{ f\left(x\right)=ax^2+bx+c }[/math] mit [math]\displaystyle{ a\neq0 }[/math] heißt quadratische Funktion in Normalform, ihr Graph heißt Parabel. [math]\displaystyle{ a }[/math] heißt Streckungsfaktor, wenn [math]\displaystyle{ |a|\gt 1 }[/math] und Stauchungsfaktor, wenn [math]\displaystyle{ |a|\lt 1 }[/math]. Für [math]\displaystyle{ a\gt 0 }[/math] ist die Parabel nach oben geöffnet, für [math]\displaystyle{ a\lt 0 }[/math] ist die Parabel nach unten geöffnet. Der tiefste bzw. höchster Punkt heißt Scheitelpunkt oder Scheitel S. Der Graph von [math]\displaystyle{ f\left(x\right)=x^2 }[/math] heißt Normalparabel.
Beispiele für quadratische Funktionen
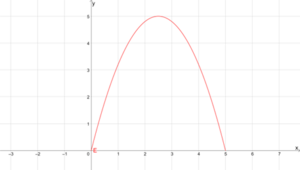
Der Graph der Funktion [math]\displaystyle{ E(x)=-0,8x^2+4x }[/math] mit dem Definitionsbereich [math]\displaystyle{ \mathbb{D}_E=[0;5] }[/math] ist auf der rechten Seite dargestellt. Der Scheitelpunkt ist [math]\displaystyle{ S(2,5|5) }[/math]. Die Normalparabel wurde um den Faktor [math]\displaystyle{ -0,8 }[/math] gestaucht und ist nach unten geöffnet. Der Schnittpunkt mit der y-Achse ist [math]\displaystyle{ (0|0) }[/math].
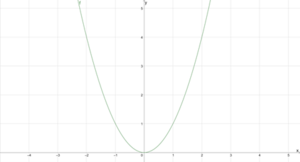
Der nächste Graph ist die Normalparabel zur Funktion [math]\displaystyle{ f(x)=x^2 }[/math] mit dem Scheitelpunkt [math]\displaystyle{ S(0|0) }[/math] und wurde daher weder gestaucht, noch gestreckt, da [math]\displaystyle{ a=1 }[/math] ist. Der Schnittpunkt mit der y-Achse ist [math]\displaystyle{ (0/0) }[/math].
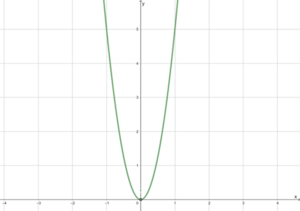
Der letzte Graph ist hat die Funktionsvorschrift [math]\displaystyle{ f(x)=5x^2 }[/math] mit dem Scheitelpunkt [math]\displaystyle{ S(0|0) }[/math] und wurde daher um 5 Einheiten gestreckt, da [math]\displaystyle{ a=5 }[/math] ist. Der Schnittpunkt mit der y-Achse ist [math]\displaystyle{ (0/0) }[/math].
Nullstellen
Die Nullstellen einer quadratischen Funktion [math]\displaystyle{ {f\left(x\right)=x}^2+px+q }[/math] werden durch Auflösen der Gleichung [math]\displaystyle{ x^2+px+q=0 }[/math] nach [math]\displaystyle{ x }[/math] ausgerechnet. Für eine Nachfragefunktion wird die positive Nullstelle auch Sättigungsmenge genannt. Die Lösung der Gleichung wird mit der p-q-Formel berechnet: [math]\displaystyle{ x_{1,2}=-\frac{p}{2}\pm\sqrt{\left(\frac{p}{2}\right)^2-q} }[/math]
Beispiel pq-Formel
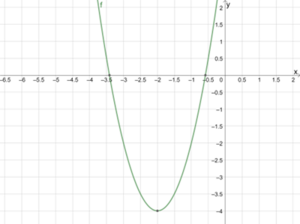
Wir betrachten [math]\displaystyle{ {f\left(x\right)=2x}^2+8x+4 }[/math]. Wir rechnen
[math]\displaystyle{ {2x}^2+8x+4=0\ |\ \div2 }[/math]
[math]\displaystyle{ x^2+4x+2=0\ }[/math]
damit wir die p-q-Formel anwenden können. Es gilt [math]\displaystyle{ p=4 }[/math] und [math]\displaystyle{ q=2 }[/math]. Diese Werte können wir einsetzen: [math]\displaystyle{ x_1=-\frac{4}{2}+\sqrt{\left(\frac{4}{2}\right)^2-2}=-2-\sqrt2\approx-3,41 }[/math] und [math]\displaystyle{ x_2=-\frac{4}{2}+\sqrt{\left(\frac{4}{2}\right)^2-2}=-2+\sqrt2\approx-0,59 }[/math]
Also hat f die Nullstellen [math]\displaystyle{ x_1\approx-3,41 }[/math] und [math]\displaystyle{ x_2\approx-0,59 }[/math]. Das sind die x-Werte, bei denen der Graph die x-Achse schneidet:
Nullstellen ohne pq-Formel berechnen
Einige Nullstellen bzw. Lösungen von quadratischen Gleichungen können auch ohne p-q-Formel bestimmt werden:
Direktes Auflösen einer quadratischen Gleichung nach x:
[math]\displaystyle{ 3\left(x-5\right)^2=27\ |\ \div3 }[/math]
[math]\displaystyle{ \left(x-5\right)^2=9\ |\ \sqrt{~} }[/math]
[math]\displaystyle{ x-5=9\ \vee x-5=-9\ |+5 }[/math]
[math]\displaystyle{ x=14\ \vee x=-4 }[/math]
Produkt von Nullstellen:
[math]\displaystyle{ \left(x-8\right)\left(x+3\right)=0 }[/math]
[math]\displaystyle{ x-8=0\ \vee x-3=0 }[/math]
[math]\displaystyle{ x=8\ \vee x=3 }[/math]
Direktes Auflösen nach x:
[math]\displaystyle{ 7x^2-343=0\ |\ \div7 }[/math]
[math]\displaystyle{ x^2-49=0\ |+49 }[/math]
[math]\displaystyle{ x^2=49\ \ |\ \sqrt{~} }[/math]
[math]\displaystyle{ x=7\ \vee x=-7\ }[/math]
Nullstellenform
Eine Funktion der Form [math]\displaystyle{ f\left(x\right)=a(x-x_1)(x-x_2) }[/math] heißt quadratische Funktion in Nullstellenform. Die Nullstellen sind [math]\displaystyle{ x_1 }[/math] und [math]\displaystyle{ x_2 }[/math].
Beispiel mit Nullstellen [math]\displaystyle{ x_1=3 }[/math] und [math]\displaystyle{ x_2=-4 }[/math]
[math]\displaystyle{ x_1=3 }[/math] und [math]\displaystyle{ x_2=-4 }[/math] sind Nullstellen von [math]\displaystyle{ f }[/math] mit [math]\displaystyle{ a=1 }[/math], dann ist [math]\displaystyle{ f\left(x\right)=1 \cdot (x-3)\cdot (x+4) }[/math] in Nullstellenform.
Beispiel mit Nullstellen [math]\displaystyle{ x_1=2 }[/math] und [math]\displaystyle{ x_2=6 }[/math]
[math]\displaystyle{ x_1=2 }[/math] und [math]\displaystyle{ x_2=6 }[/math] sind Nullstellen von [math]\displaystyle{ g }[/math] mit [math]\displaystyle{ a=-3 }[/math], dann ist [math]\displaystyle{ g\left(x\right)=(-3)\cdot (x-2) \cdot (x-6) }[/math] in Nullstellenform.
Scheitelpunktform
Eine Funktion der Form [math]\displaystyle{ f\left(x\right)=a({x-e)}^2+f }[/math] mit [math]\displaystyle{ a\neq0 }[/math] heißt quadratische Funktion in Scheitelpunktform. Der Scheitelpunkt ist [math]\displaystyle{ S(e|f) }[/math]. Der Faktor [math]\displaystyle{ a }[/math] ist in der Scheitelpunktform und der Normalform der Gleiche.
Beispiel
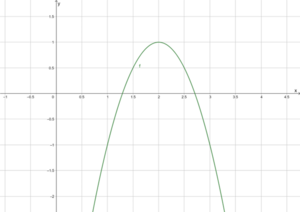
Wir betrachten die Funktion [math]\displaystyle{ f\left(x\right)=-2({x-2)}^2+1 }[/math]. Der Scheitelpunkt ist dann [math]\displaystyle{ S(2|1) }[/math]. Man kann die rechte Seite der Funktion weiter auflösen, um von der Scheitelpunktform zur Normalform zu kommen:
[math]\displaystyle{ f\left(x\right)=-2({x-2)}^2+1 }[/math]
[math]\displaystyle{ f\left(x\right)=-2(x^2-4x+4)+1 }[/math]
[math]\displaystyle{ f\left(x\right)=-2x^2+8x-8+1 }[/math]
[math]\displaystyle{ f\left(x\right)=-2x^2+8x-7 }[/math]
Der Graph der Funktion ist auf der rechten Seite aufgelistet. Der Schnittpunkt mit der y-Achse ist [math]\displaystyle{ (0|-7) }[/math].