Differenzenquotient: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „==Definition== mini|Passante, Tangente, Sekante an der Normalparabel Ist <math>f</math> eine Funktion, die auf dem Intervall <math>[x_0;x_1] \subseteq \mathbb{D}</math> definiert ist, dann heißt <math>\frac{f(x_1)-f(x_0)}{x_1-x_0}</math> '''Differenzenquotient''' von <math>f</math> im Intervall <math>[x_0;x_1]</math>. Bei Anwendungen wird der Differe…“ |
Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Definition== | ==Definition== | ||
[[Datei:DifferentialrechnungTangentePassSek.png|mini|Passante, Tangente, Sekante an der Normalparabel]] | [[Datei:DifferentialrechnungTangentePassSek.png|mini|Passante, Tangente, Sekante an der Normalparabel]] | ||
Ist <math>f</math> eine [[Funktion]], die auf dem Intervall <math>[x_0;x_1] \subseteq \mathbb{D}</math> [[Funktion#Definitions-_und_Wertebereichdefiniert|definiert]] ist, dann heißt <math>\frac{f(x_1)-f(x_0)}{x_1-x_0}</math> '''Differenzenquotient''' von <math>f</math> im Intervall <math>[x_0;x_1]</math>. Bei Anwendungen wird der Differenzenquotient auch als '''mittlere Änderungsrate''' bezeichnet. | Ist <math>f</math> eine [[Funktion]], die auf dem Intervall <math>[x_0;x_1] \subseteq \mathbb{D}_f</math> [[Funktion#Definitions-_und_Wertebereichdefiniert|definiert]] ist, dann heißt <math>\frac{f(x_1)-f(x_0)}{x_1-x_0}</math> '''Differenzenquotient''' von <math>f</math> im Intervall <math>[x_0;x_1]</math>. Bei Anwendungen wird der Differenzenquotient auch als '''mittlere Änderungsrate''' bezeichnet. | ||
Bei einer [[Lineare_Funktion#Punktsteigungsform_ermitteln|linearen Funktion]] <math>f</math> und zwei Punkten <math>P(x_0| f(x_0))</math> und <math>Q(x_1|f(x_1))</math> wird mit dem Differenzenquotient die Steigung von <math>f</math> berechnet. | Bei einer [[Lineare_Funktion#Punktsteigungsform_ermitteln|linearen Funktion]] <math>f</math> und zwei Punkten <math>P(x_0| f(x_0))</math> und <math>Q(x_1|f(x_1))</math> wird mit dem Differenzenquotient die Steigung von <math>f</math> berechnet. | ||
| Zeile 16: | Zeile 16: | ||
Eine Gerade, die den Graphen einer [[Funktion]] <math>f</math> in genau einem Punkt schneidet heißt '''Tangente'''. Die [[Lineare_Funktion#Definition|Steigung]] der Tangente in einem Punkt bezeichnen wir dann als die [[Lineare_Funktion#Definition|Steigung]] in diesem Punkt. Die Tangente erhalten wir, indem wir die Sekante durch die Punkte <math>P</math> und <math>Q</math> ermitteln und die Punkte immer näher aneinanderschieben, bis sie aufeinander liegen. | Eine Gerade, die den Graphen einer [[Funktion]] <math>f</math> in genau einem Punkt schneidet heißt '''Tangente'''. Die [[Lineare_Funktion#Definition|Steigung]] der Tangente in einem Punkt bezeichnen wir dann als die [[Lineare_Funktion#Definition|Steigung]] in diesem Punkt. Die Tangente erhalten wir, indem wir die Sekante durch die Punkte <math>P</math> und <math>Q</math> ermitteln und die Punkte immer näher aneinanderschieben, bis sie aufeinander liegen. | ||
[[Kategorie:Differentialrechnung]] | [[Kategorie:Differentialrechnung]] | ||
Aktuelle Version vom 10. Juli 2024, 11:42 Uhr
Definition
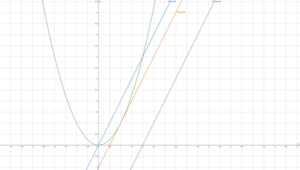
Ist [math]\displaystyle{ f }[/math] eine Funktion, die auf dem Intervall [math]\displaystyle{ [x_0;x_1] \subseteq \mathbb{D}_f }[/math] definiert ist, dann heißt [math]\displaystyle{ \frac{f(x_1)-f(x_0)}{x_1-x_0} }[/math] Differenzenquotient von [math]\displaystyle{ f }[/math] im Intervall [math]\displaystyle{ [x_0;x_1] }[/math]. Bei Anwendungen wird der Differenzenquotient auch als mittlere Änderungsrate bezeichnet.
Bei einer linearen Funktion [math]\displaystyle{ f }[/math] und zwei Punkten [math]\displaystyle{ P(x_0| f(x_0)) }[/math] und [math]\displaystyle{ Q(x_1|f(x_1)) }[/math] wird mit dem Differenzenquotient die Steigung von [math]\displaystyle{ f }[/math] berechnet.
Geraden zu Funktionen
Definition Passante
Eine Gerade, die den Graphen einer Funktion [math]\displaystyle{ f }[/math] in keinem Punkt schneidet heißt Passante.
Sekante
Eine Gerade, die den Graphen einer Funktion [math]\displaystyle{ f }[/math] in genau zwei Punkten schneidet heißt Sekante. Die Steigung einer Sekante durch die Punkte [math]\displaystyle{ P }[/math] und [math]\displaystyle{ Q }[/math] wird mit dem Differenzenquotient ermittelt.
Tangente
Eine Gerade, die den Graphen einer Funktion [math]\displaystyle{ f }[/math] in genau einem Punkt schneidet heißt Tangente. Die Steigung der Tangente in einem Punkt bezeichnen wir dann als die Steigung in diesem Punkt. Die Tangente erhalten wir, indem wir die Sekante durch die Punkte [math]\displaystyle{ P }[/math] und [math]\displaystyle{ Q }[/math] ermitteln und die Punkte immer näher aneinanderschieben, bis sie aufeinander liegen.