Aktivitätsdiagramm: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „Das '''Aktivitätsdiagramm''' (auch '''Ablaufdiagramm''') ist ein Verhaltensdiagramm und eine der vierzehn Diagrammarten in der Unified Modeling Language (UML). Es dient zur übersichtlichen Darstellung von Abläufen und wird sowohl in der Analyse- als auch in der Designphase von Softwareentwicklungsprozessen eingesetzt. == Einführung == Das Aktivitätsdiagramm beschreibt allgemein Abläufe und stellt dar, in welcher Reihenfolge bestimmte Aktionen a…“ |
|||
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
Das Aktivitätsdiagramm beschreibt allgemein Abläufe und stellt dar, in welcher Reihenfolge bestimmte Aktionen ausgeführt werden. Eine '''Aktion''' ist ein einzelner Schritt innerhalb einer '''Aktivität'''. Eine Aktivität kann folgendes repräsentieren: | Das Aktivitätsdiagramm beschreibt allgemein Abläufe und stellt dar, in welcher Reihenfolge bestimmte Aktionen ausgeführt werden. Eine '''Aktion''' ist ein einzelner Schritt innerhalb einer '''Aktivität'''. Eine Aktivität kann folgendes repräsentieren: | ||
Einen fachlichen oder betriebswirtschaftlichen Prozess | *Einen fachlichen oder betriebswirtschaftlichen Prozess | ||
*Einen Anwendungsfall (Use Case) | |||
Einen | *Den Algorithmus einer oder mehrerer Methoden im Sinne eines [[Programmablaufplan]]s (PAP) | ||
Den Algorithmus einer oder mehrerer Methoden im Sinne eines [[Programmablaufplan]]s (PAP) | |||
== Aufbau == | == Aufbau == | ||
[[Datei:Aktivitätsdiagramm-Elemente.png|mini|Elemente eines Aktivitätsdiagramms]] | |||
In der nebenstehenden Grafik werden die wichtigsten Bestandteile eines Aktivitätsdiagramms vorgestellt. | |||
=== Knoten === | === Knoten === | ||
Alle Elemente des Aktivitätsdiagramms, die verbunden werden, werden allgemein als '''Knoten''' bezeichnet. Dazu zählen: | Alle Elemente des Aktivitätsdiagramms, die verbunden werden, werden allgemein als '''Knoten''' bezeichnet. Dazu zählen: | ||
Start- und Endpunkte | *Start- und Endpunkte | ||
*Verzweigungen und Zusammenführungen | |||
Verzweigungen und Zusammenführungen | *Splittungen und Synchronisationen | ||
*Aktionen | |||
Splittungen und Synchronisationen | *Objekte | ||
Aktionen | |||
Objekte | |||
=== Start- und Endpunkt === | === Start- und Endpunkt === | ||
| Zeile 35: | Zeile 30: | ||
Das Token wandert nach dem Start die erste Verbindungslinie entlang zum ersten Knoten. Nach Ausführung der dort definierten Aktion wandert es entlang der ausgehenden Kante zum nächsten Knoten usw. Das Token markiert den aktuellen Stand der Ablaufausführung. Der Ablauf setzt sich fort, bis ein Endpunkt erreicht ist, wo das Token zerstört wird. | Das Token wandert nach dem Start die erste Verbindungslinie entlang zum ersten Knoten. Nach Ausführung der dort definierten Aktion wandert es entlang der ausgehenden Kante zum nächsten Knoten usw. Das Token markiert den aktuellen Stand der Ablaufausführung. Der Ablauf setzt sich fort, bis ein Endpunkt erreicht ist, wo das Token zerstört wird. | ||
<html> | |||
<iframe width="280" height="157.5" src="https://www.youtube.com/embed/rlNckXwO6fs?si=so6bGduWe0TDMTPO" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" referrerpolicy="strict-origin-when-cross-origin" allowfullscreen></iframe> | |||
</html> | |||
=== Aktion === | === Aktion === | ||
Der wichtigste Knotentyp ist die '''Aktion'''. Aktionen stellen die einzelnen, nicht weiter teilbaren Schritte einer Aktivität dar und werden als Rechteck mit abgerundeten Ecken dargestellt. Eine Aktion wird durch genau eine eingehende Kante aktiviert und nach ihrer Ausführung verlässt genau eine Kante die Aktion. | Der wichtigste Knotentyp ist die '''Aktion'''. Aktionen stellen die einzelnen, nicht weiter teilbaren Schritte einer Aktivität dar und werden als Rechteck mit abgerundeten Ecken dargestellt. Eine Aktion wird durch genau eine eingehende Kante aktiviert und nach ihrer Ausführung verlässt genau eine Kante die Aktion. | ||
| Zeile 56: | Zeile 54: | ||
== Beispiel == | == Beispiel == | ||
Es soll ein Algorithmus entwickelt werden, um den | [[Datei:Aktivitätsdiagramm-GGT-berechnen.png|mini|Aktivitätsdiagramm GGT ermitteln]] | ||
Es soll ein Algorithmus entwickelt werden, um den größten gemeinsamen Teiler (GGT) zweier ganzzahliger Werte zu ermitteln. Der GGT zweier Werte m und n ist im günstigen Fall m/2 bzw. n/2, im ungünstigen Fall 1. Hat der GGT den Wert 1, werden die beiden Zahlen als [[Teilerfremdheit|teilerfremd]] bezeichnet. | |||
[[Kategorie:Modellierung]] | [[Kategorie:Modellierung]] | ||
[[Kategorie:FI_I_SDM]] | [[Kategorie:FI_I_SDM]] | ||
Aktuelle Version vom 17. September 2025, 09:14 Uhr
Das Aktivitätsdiagramm (auch Ablaufdiagramm) ist ein Verhaltensdiagramm und eine der vierzehn Diagrammarten in der Unified Modeling Language (UML). Es dient zur übersichtlichen Darstellung von Abläufen und wird sowohl in der Analyse- als auch in der Designphase von Softwareentwicklungsprozessen eingesetzt.
Einführung
Das Aktivitätsdiagramm beschreibt allgemein Abläufe und stellt dar, in welcher Reihenfolge bestimmte Aktionen ausgeführt werden. Eine Aktion ist ein einzelner Schritt innerhalb einer Aktivität. Eine Aktivität kann folgendes repräsentieren:
- Einen fachlichen oder betriebswirtschaftlichen Prozess
- Einen Anwendungsfall (Use Case)
- Den Algorithmus einer oder mehrerer Methoden im Sinne eines Programmablaufplans (PAP)
Aufbau
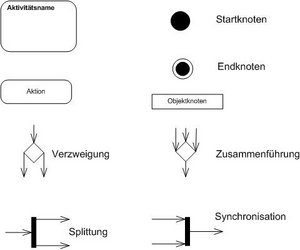
In der nebenstehenden Grafik werden die wichtigsten Bestandteile eines Aktivitätsdiagramms vorgestellt.
Knoten
Alle Elemente des Aktivitätsdiagramms, die verbunden werden, werden allgemein als Knoten bezeichnet. Dazu zählen:
- Start- und Endpunkte
- Verzweigungen und Zusammenführungen
- Splittungen und Synchronisationen
- Aktionen
- Objekte
Start- und Endpunkt
Ein Aktivitätsdiagramm hat einen oder mehrere Start- und Endpunkte. Diese sind über Knoten und Kanten miteinander verbunden.
Kanten
Kanten verbinden Knoten zu einem Ablauf und werden durch Pfeile dargestellt. Wenn eine Aktivität ausgelöst wird, beginnt ein sogenanntes Token durch den definierten Ablauf zu wandern.
Token
Das Token wandert nach dem Start die erste Verbindungslinie entlang zum ersten Knoten. Nach Ausführung der dort definierten Aktion wandert es entlang der ausgehenden Kante zum nächsten Knoten usw. Das Token markiert den aktuellen Stand der Ablaufausführung. Der Ablauf setzt sich fort, bis ein Endpunkt erreicht ist, wo das Token zerstört wird.
Aktion
Der wichtigste Knotentyp ist die Aktion. Aktionen stellen die einzelnen, nicht weiter teilbaren Schritte einer Aktivität dar und werden als Rechteck mit abgerundeten Ecken dargestellt. Eine Aktion wird durch genau eine eingehende Kante aktiviert und nach ihrer Ausführung verlässt genau eine Kante die Aktion.
Objekt
Objektknoten werden als Rechteck ohne abgerundete Ecken dargestellt und symbolisieren Datenspeicher, die Instanzen in der Objektorientierung entsprechen. Befindet sich ein Objektknoten zwischen zwei Aktionen, transportiert das Token Daten von der ausgehenden Aktion in den Speicher und von dort in die nächste Aktion.
Durch die Kombination von Aktionen mit Objektknoten können Methoden abgebildet werden, wobei eine Aktion eine Rückgabe erzeugt, die als Eingabe an die nächste Aktion übergeben wird.
Verzweigung
Eine Raute stellt eine Verzweigung dar. Welchen Weg das Token einschlägt, hängt von der in der Raute formulierten Bedingung und den definierten Eingangsbedingungen für die jeweiligen Kanten ab. Ist eine Bedingung erfüllt, wird das Token auf genau einer der ausgehenden Kanten weitergeleitet.
Gabelung (Splittung)
Ein schwarzer Balken symbolisiert eine Gabelung (Splittung). Dieser Knotentyp kann verwendet werden, um:
Eine Verbindungslinie aufzuteilen (beim Verlassen des Balkens)
Mehrere Verbindungslinien zu einer zusammenzuführen (beim Eintritt in den Balken)
Bei einer Gabelung wird das Token kopiert, und auf jeder ausgehenden Kante wandert eine Kopie weiter. Bei der Zusammenführung muss ein Token, das auf einer eingehenden Kante ankommt, warten, bis auf allen eingehenden Kanten ein Token angekommen ist - erst dann wird auf der ausgehenden Kante ein Token weitergeschickt.
Beispiel
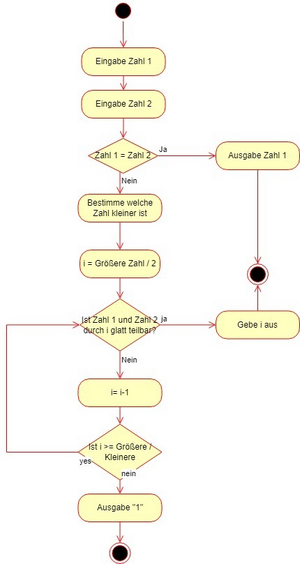
Es soll ein Algorithmus entwickelt werden, um den größten gemeinsamen Teiler (GGT) zweier ganzzahliger Werte zu ermitteln. Der GGT zweier Werte m und n ist im günstigen Fall m/2 bzw. n/2, im ungünstigen Fall 1. Hat der GGT den Wert 1, werden die beiden Zahlen als teilerfremd bezeichnet.