Endlicher Automat: Unterschied zwischen den Versionen
Thomas (Diskussion | Beiträge) Die Seite wurde neu angelegt: „== Einführung == Ein endlicher Automat (EA, auch Zustandsmaschine, Zustandsautomat; englisch finite state machine, FSM) ist ein mathematisches Modell eines Systems mit diskreten Ein- und Ausgaben. Diskret bedeutet, dass zu jedem Zeitpunkt nur eine Eingabe und eine Ausgabe verarbeitet wird. Es gibt eine endliche Anzahl ein Ein- und Ausgaben. Das durch den Automaten beschriebene System befindet sich in einer endlichen Anzahl von Zuständen. Das Verhalten d…“ |
Thomas (Diskussion | Beiträge) |
||
| (8 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== Einführung == | == Einführung == | ||
Ein endlicher Automat (EA, auch Zustandsmaschine, Zustandsautomat; englisch finite state machine, FSM) ist ein mathematisches Modell eines Systems mit diskreten Ein- und Ausgaben. Diskret bedeutet, dass zu jedem Zeitpunkt nur eine Eingabe und eine Ausgabe verarbeitet wird. Es gibt eine endliche Anzahl ein Ein- und Ausgaben. Das durch den Automaten beschriebene System befindet sich in einer endlichen Anzahl von Zuständen. Das Verhalten des Systems wird durch Zustände, Zustandsübergängen und Aktionen beschrieben. | Ein endlicher Automat (EA, auch Zustandsmaschine, Zustandsautomat; englisch finite state machine, FSM) ist ein mathematisches Modell eines Systems mit diskreten Ein- und Ausgaben. Diskret bedeutet, dass zu jedem Zeitpunkt nur eine Eingabe und eine Ausgabe verarbeitet wird. Es gibt eine endliche Anzahl ein Ein- und Ausgaben. Das durch den Automaten beschriebene System befindet sich in einer endlichen Anzahl von Zuständen. Das Verhalten des Systems wird durch Zustände, Zustandsübergängen und Aktionen beschrieben. | ||
Automaten lassen sich unteranderem durch ein [[Zustandsdiagramm|UML Zustandsdiagramm]] darstellen. | |||
== Motivation == | == Motivation == | ||
| Zeile 37: | Zeile 39: | ||
Bonbonautomat als Mealy Automat: A = {Q,s,∑,Ω, δ, λ} | Bonbonautomat als Mealy Automat: A = {Q,s,∑,Ω, δ, λ} | ||
=== | [[Datei:Grafische Darstellung Mealy-Automat Bonbons.jpg|mini]] | ||
== Übergangsfunktion == | |||
Die Übergangsfunktion δ:Qx∑ ->Q ordnet jeder Kombination aus einem Zustand (erste Spalte) und einem Eingabezeichen (erste Zeile) einen Nachfolgezustand (Matrix) zu. Dies lässt sich sehr gut tabellarisch darstellen: | |||
M: Münze einwerfen | |||
H: Hebel drehen | |||
B: Bonbon ausgeben | |||
N: Keine Ausgabe | |||
Gäbe es einen Endzustand, würde dieser in der Tabelle mit einem Stern kenntlich gemacht. | |||
Beispiel Übergangsfunktion für den Bonbonautomat: | |||
[[Datei:Tabelle Übergangsfunktion.png|mini]] | |||
== DEA - Deterministischer endlicher Automat == | |||
=== Definition === | |||
Ein Automat heißt deterministisch, wenn für jeden seiner Zustände für jedes Eingabezeichen nur genau ein Folgezustand existiert. Das Verhalten des Automaten ist somit eindeutig bestimmt. Der deterministische endliche Automat ist genau wie der Mealy-Automat dadurch gekennzeichnet, dass er eine endliche Menge an Zuständen besitzt und die Übergänge von einem Zustand zum anderen deterministisch definiert sind, es also keine Wahlmöglichkeiten für den Zustandswechsel bei einer konkreten Eingabe gibt. Er besitzt jedoch kein Ausgabealphabet und keine Ausgabefunktion, dafür aber eine Menge an akzeptierenden Endzuständen. | |||
Bildlich kann man sich den DEA wie eine Blackbox vorstellen, die sich einem Zustand S befindent und eine Folge von Buchstaben aus ∑ liest. Der DEA geht die Buchstaben einzeln durch bis ein Wort entsteht und gemäß Zustandsübergangsfunktion einen Folgezustand erreicht wird, der einen definierten Endzustand für den DEA darstellt. | |||
Solche DEA können z. B. überprüfen, ob in einer Kaffeemaschine das Kaffeeersatzfach geleert werden muss. Dazu muss eine Spezifikation des Problems vorliegen, anhand derer sich das Problem als deterministischer Automat formalisieren lässt. | |||
Formal definiert man einen DEA als 5-Tupel A = {Q,s,∑,F, δ}: | |||
Q ist eine nicht leere, endliche Menge von Zuständen | |||
s∈Q ist der Startzustand | |||
∑ ist ein nicht leeres, endliches Eingabealphabet | |||
F die Menge der zu akzeptierenden Endzustände, wobei F eine Teilmenge von von Q ist. | |||
δ:Qx∑ ->Q ist die Übergangsfunktion, die jeder Kombination aus einem Zustand und einem Eingabezeichen einen Nachfolgezustand zuordnet. | |||
[[Datei:DEA Kaffeeautomat.jpg|mini]] | |||
Nichtdeterministischer endlicher Automat | |||
=== Definition === | |||
Ein nichtdeterministischer endlicher Automat (NEA; englisch nondeterministic finite automaton, NFA) ist ein endlicher Automat, bei dem es für den Zustandsübergang mehrere gleichwertige Möglichkeiten gibt. Im Unterschied zum deterministischen endlichen Automaten sind die Möglichkeiten nicht eindeutig, dem Automaten ist also nicht vorgegeben, welchen Übergang er zu wählen hat. | |||
Formal kann ein NEA A als (5-Tupel ( Q , Σ , Δ , S , F) definiert werden. Hierbei gilt Folgendes: | |||
Q ist eine nicht leere, endliche Menge von Zuständen | |||
s∈Q ist der Startzustand | |||
∑ ist ein nicht leeres, endliches Eingabealphabet | |||
F die Menge der zu akzeptierenden Endzustände, wobei F eine Teilmenge von von Q ist. | |||
δ:Qx∑ ->Q ist die Übergangsfunktion, die jeder Kombination aus einem Zustand und einem Eingabezeichen einen Nachfolgezustand zuordnet. | |||
Zudem gilt das Wort W zur Sprache L des Automaten gehört. wenn W ∈ ∑ ist und zu einem Endzustand F führt. | |||
=== Beispiel === | |||
[[Datei:Nichtdeterministischer endlicher Automat NEA.jpg|mini]] | |||
Folgendes Diagramm stellt NEA und DEA gegenüber. Es wurde ein einfacher Spam-Filter als Automat entwickelt. | |||
== Potenzmengenkonstruktion == | |||
Die Potenzmengenkonstruktion ist ein Verfahren, das einen nichtdeterministischen endlichen Automaten (NEA) in einen äquivalenten deterministischen endlichen Automaten (DEA) umwandelt. | |||
Die Zustände des aus dem NEA abzuleitenden DEA sind Mengen von Zuständen des NEA. Ein Zustand vom DEA kodiert dabei all diejenigen Zustände, in denen sich der äquivalente nichtdeterministische Automat NEA zu einem bestimmten Zeitpunkt befinden könnte. Ein Zustandsübergang im DEA ist deterministisch, da sein Folgezustand aus der Menge aller möglichen Folgezustände besteht, in die ein NEA unter einer bestimmten Eingabe gelangen kann. Das Verfahren heißt Potenzmengenkonstruktion, weil die Zustände des konstruierten Automaten Mengen von Zuständen des Ausgangsautomaten sind und daher die konstruierte Zustandsmenge Teil der Potenzmenge der Zustandsmenge des Ausgangsautomaten ist. | |||
Wir bertachten folgenden NEA als 5-Tupel (Quelle: https://de.wikipedia.org/wiki/Potenzmengenkonstruktion#Beispiele) | |||
[[Datei:5Tupel.png|mini]] | |||
Q: S0,S1,S2,S3 | |||
S0∈Q | |||
∑:a,b | |||
F: S3 | |||
δ:Qx∑ ->Q | |||
Die Übergangsfunktion des NEA lässt sich durch folgenden Graph beschreiben: | |||
[[Datei:NEA Beispiel.png|mini]] | |||
Nach obiger Konstruktion ergeben sich die Zustandsmenge Q′={S0′,S1′,S2′,S3′} und die Übertragungsfunktion δ′ des äquivalenten deterministischen Automaten wie folgt: | |||
[[Datei:DEA Beipsiel.png|mini]] | |||
Neue Finalzustände sind die Zustände, die den Finalzustand des ursprünglichen NEA enthalten. Hier also S3′, da S3′ s3 enthält. Möglich ist, dass der abgeleitete DEA mehr Finalzustände besitzt als der zugrundeliegende NEA, da alle neuen Zustandsmengen die einen alten Finalzustände enthalten nun Endzustände sind. Insgesamt ergibt sich der deterministische Automat , der folgende graphische Darstellung besitzt: | |||
[[Datei:DEA Graph.png|mini]] | |||
== ε-NEA == | |||
ε-NEAs sind ein nützliches Werkzeug in der Theorie formaler Sprachen und Automatentheorie. Sie bieten Flexibilität und können in vielen Fällen den Design- und Analyseprozess vereinfachen, da Sie es ermöglichen, Zustände ohne das Verarbeiten eines Symbols zu wechseln. Das kann in manchen Situationen die Konstruktion eines Automaten erleichtern. In manchen Fällen kann ein ε-NEA eine kompaktere und klarere Darstellung eines Problems oder einer Sprache bieten als ein NEA oder DEA. | |||
Um die Darstellung von endlichen Automaten zu vereinfachen, können Zustandsübergänge ohne Einlesen eines Zeichens ausgelöst werden. Diese Zustandsübergänge bezeichnet man als Epsilon-Übergänge. Für jeden nichtdeterministischen endlichen Automaten mit Epsilon-Übergängen gibt es einen nichtdeterministischen endlichen Automaten ohne Epsilon-Übergänge, der dieselbe Sprache erkennt, und umgekehrt. Die beiden Maschinenmodelle sind also äquivalent. Genau wie der normale nichtdeterministische endliche Automat erkennt ein nichtdeterministischer endlicher Automat mit Epsilon-Übergängen ein Wort w, wenn es in seinem Zustandsgraphen einen Pfad vom Startzustand zu einem Endzustand gibt. | |||
=== Umwandlung ε-NEA zu NEA === | |||
Jeder ε-NEA lässt sich in einen NEA ohne ε-Übergänge umwandeln. Hierfür entfernt man die ε-Übergänge und betrachtet die Zustandsmengen, die von den Zuständen Q inklusive ε-Übergänge erreicht werden können. Für diese resultierenden Zustandsmengen wird analog zum Verfahren der Potenzmengenkonstruktion ein NEA ohne ε-Übergänge abgeleitet. | |||
=== Beispiel === | |||
Das folgende Diagramm beschreibt einen NEA mit ε-Übergängen. Dieser Automat lässt sich als 5-Tupel beschreiben (Quelle: https://hwlang.de/theor/index.htm): | |||
[[Datei:ENEA.png|mini]] | |||
Q: 0-7 | |||
S∈2 | |||
∑:a,b,ε | |||
F: 3 | |||
δ:Qx∑ ->Q | |||
Er wird in der Folge in einen NEA ohne ε-Übergänge umgewandelt. | |||
[[Kategorie:Automaten]] | |||
[[Kategorie:AHR_I_Informatik_LK]] | |||
Aktuelle Version vom 29. August 2025, 13:54 Uhr
Einführung
Ein endlicher Automat (EA, auch Zustandsmaschine, Zustandsautomat; englisch finite state machine, FSM) ist ein mathematisches Modell eines Systems mit diskreten Ein- und Ausgaben. Diskret bedeutet, dass zu jedem Zeitpunkt nur eine Eingabe und eine Ausgabe verarbeitet wird. Es gibt eine endliche Anzahl ein Ein- und Ausgaben. Das durch den Automaten beschriebene System befindet sich in einer endlichen Anzahl von Zuständen. Das Verhalten des Systems wird durch Zustände, Zustandsübergängen und Aktionen beschrieben.
Automaten lassen sich unteranderem durch ein UML Zustandsdiagramm darstellen.
Motivation
Computer, andere Maschinen oder Programme erscheinen im Alltag oft als eine Black Box, egal ob sie triviale oder schwierige Probleme lösen. Sie reagieren auf Eingaben, verarbeiten Informationen, ohne dass wir sehen, wie, und präsentieren eine Antwort bzw. eine Lösung. Manchmal scheinen Sie sogar ‚intelligenter‘ als Menschen zu sein, wenn sie gegen Schachweltmeister gewinnen, die 2,7 Billionen Nachkommastellen von n berechnen, einem sagen, was man als Nächstes kaufen möchte oder man mit einem Computer spricht, ohne es zu bemerken.
Doch das Verarbeiten der Eingaben ist weder Zauberei, noch (zumindest bis heute) intelligentes Vorgehen. Es sind Programme, die das Verhalten der Maschine bestimmen, und diese Maschinen lassen sich sogar durch einfach strukturierte Modelle wie den endlichen Automaten beschreiben. Die Einfachheit des Modells sollte aber nicht über deren Mächtigkeit hinwegtäuschen. Das Automatenmodell dient zum Beispiel der Zellforschung als probates Mittel, um das Verhalten von Zellen zu beschreiben, und auch die Hirnforschung greift bei der Beschreibung des Gehirns durch neurale Netze darauf zurück. Automaten findet man außerdem in zahlreichen Alltagssituationen vor: Fahrstühle, Ampel Waschmaschinen, Getränke, Fahrkarten- und Geldautomaten sind nur einige der vielen Maschinen, die von einem endlichen Automaten gesteuert werden.
Diese Automaten werden als endlich bezeichnet, weil die Menge der Eingaben, der Ausgaben und der Zustände, die sie durchlaufen, endlich sind. Folgt ein Automat folgender formalen Beschreibung, dann bezeichnet man diesen als Mealy-Automat.
Mealy-Automat
Definition
Für die Formalisierung des Automaten führt man zunächst die Ein- und Ausgabe ein. Sie werden als Eingabe und Ausgabealphabet bezeichnet. Der Begriff erklärt sich aus der Tatsache, dass Computer in der Regel Texte, also Zeichenfolgen eines Alphabets verarbeiten. Auch die Verarbeitung in einem Computer kann, da sie durch 0 und 1 repräsentiert wird, als die Verarbeitung von Texten angesehen werden.
Des Weiteren muss der Automat durch eine Zustandsmenge speichern, welche Eingaben bisher getätigt wurden. Die Zustände werden oft mit q0 ... qn bezeichnet. Mithilfe der Übergangsfunktion wird die zeitliche Abfolge der Ereignisse festgelegt. Die Übergangsfunktion gibt an, was welche Eingabe in jedem Zustand bewirkt. Neben der Übergangsfunktion gibt es noch die Ausgabefunktion, die angibt, welche Ausgabe durch die jeweilige Eingabe in einem Zustand ausgelöst wird. Die Übergangs- und Ausgabefunktionen werden tabellarisch oder grafisch als sogenannter Transitionsgraph oder Übergangsgraph dargestellt. Ein solcher Automat wird in der lnformatik als Mealy-Automat bezeichnet.
Formal definiert man einen Mealy-Automat als 6-Tupel A = {Q,s,∑,Ω, δ, λ}
Q ist eine nicht leere, endliche Menge von Zuständen
s∈Q ist der Startzustand
∑ ist ein nicht leeres, endliches Eingabealphabet
Ω ist ein nicht leeres, endliches Ausgabealphabet
δ:Qx∑ ->Q ist die Übergangsfunktion, die jeder Kombination aus einem Zustand und einem Eingabezeichen einen Nachfolgezustand zuordnet.
λ:Qx∑->Ω ist die Ausgabefunktion, die jeder Kombination aus einem Zustand und einem Eingabezeichen eine Ausgabe zuordnet.
Beispiel
Die Funktionsweise eines endlichen Automaten lässt sich leicht an einer einfachen Maschine wie einem Bonbonautomaten erläutern. Der Bonbonautomat lässt sich in seiner Funktionsweise wie folgt beschreiben. Die Eingabe besteht aus der richtigen Münze und dem Drehen des Hebels. Die Verarbeitung erfolgt im Inneren des Automaten und führt zur Ausgabe, dem Bonbon im Ausgabefach.
Die Eingabemöglichkeiten des Automaten sind begrenzt, es kommt jedoch auf die korrekte Reihenfolge an. Dreht man zuerst den Hebel und wirft dann die korrekte Münze ein, so erhält man nicht die gewünschte Ausgabe. Dazu wäre ein weiteres Drehen des Hebels erforderlich.
Bonbonautomat als Mealy Automat: A = {Q,s,∑,Ω, δ, λ}
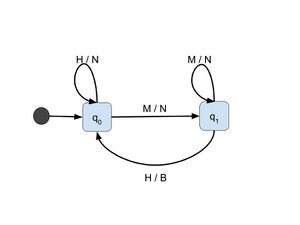
Übergangsfunktion
Die Übergangsfunktion δ:Qx∑ ->Q ordnet jeder Kombination aus einem Zustand (erste Spalte) und einem Eingabezeichen (erste Zeile) einen Nachfolgezustand (Matrix) zu. Dies lässt sich sehr gut tabellarisch darstellen:
M: Münze einwerfen
H: Hebel drehen
B: Bonbon ausgeben
N: Keine Ausgabe
Gäbe es einen Endzustand, würde dieser in der Tabelle mit einem Stern kenntlich gemacht.
Beispiel Übergangsfunktion für den Bonbonautomat:

DEA - Deterministischer endlicher Automat
Definition
Ein Automat heißt deterministisch, wenn für jeden seiner Zustände für jedes Eingabezeichen nur genau ein Folgezustand existiert. Das Verhalten des Automaten ist somit eindeutig bestimmt. Der deterministische endliche Automat ist genau wie der Mealy-Automat dadurch gekennzeichnet, dass er eine endliche Menge an Zuständen besitzt und die Übergänge von einem Zustand zum anderen deterministisch definiert sind, es also keine Wahlmöglichkeiten für den Zustandswechsel bei einer konkreten Eingabe gibt. Er besitzt jedoch kein Ausgabealphabet und keine Ausgabefunktion, dafür aber eine Menge an akzeptierenden Endzuständen.
Bildlich kann man sich den DEA wie eine Blackbox vorstellen, die sich einem Zustand S befindent und eine Folge von Buchstaben aus ∑ liest. Der DEA geht die Buchstaben einzeln durch bis ein Wort entsteht und gemäß Zustandsübergangsfunktion einen Folgezustand erreicht wird, der einen definierten Endzustand für den DEA darstellt.
Solche DEA können z. B. überprüfen, ob in einer Kaffeemaschine das Kaffeeersatzfach geleert werden muss. Dazu muss eine Spezifikation des Problems vorliegen, anhand derer sich das Problem als deterministischer Automat formalisieren lässt.
Formal definiert man einen DEA als 5-Tupel A = {Q,s,∑,F, δ}:
Q ist eine nicht leere, endliche Menge von Zuständen
s∈Q ist der Startzustand
∑ ist ein nicht leeres, endliches Eingabealphabet
F die Menge der zu akzeptierenden Endzustände, wobei F eine Teilmenge von von Q ist.
δ:Qx∑ ->Q ist die Übergangsfunktion, die jeder Kombination aus einem Zustand und einem Eingabezeichen einen Nachfolgezustand zuordnet.
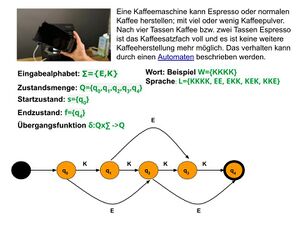
Nichtdeterministischer endlicher Automat
Definition
Ein nichtdeterministischer endlicher Automat (NEA; englisch nondeterministic finite automaton, NFA) ist ein endlicher Automat, bei dem es für den Zustandsübergang mehrere gleichwertige Möglichkeiten gibt. Im Unterschied zum deterministischen endlichen Automaten sind die Möglichkeiten nicht eindeutig, dem Automaten ist also nicht vorgegeben, welchen Übergang er zu wählen hat.
Formal kann ein NEA A als (5-Tupel ( Q , Σ , Δ , S , F) definiert werden. Hierbei gilt Folgendes:
Q ist eine nicht leere, endliche Menge von Zuständen
s∈Q ist der Startzustand
∑ ist ein nicht leeres, endliches Eingabealphabet
F die Menge der zu akzeptierenden Endzustände, wobei F eine Teilmenge von von Q ist.
δ:Qx∑ ->Q ist die Übergangsfunktion, die jeder Kombination aus einem Zustand und einem Eingabezeichen einen Nachfolgezustand zuordnet.
Zudem gilt das Wort W zur Sprache L des Automaten gehört. wenn W ∈ ∑ ist und zu einem Endzustand F führt.
Beispiel
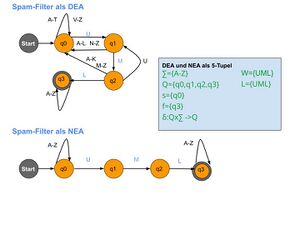
Folgendes Diagramm stellt NEA und DEA gegenüber. Es wurde ein einfacher Spam-Filter als Automat entwickelt.
Potenzmengenkonstruktion
Die Potenzmengenkonstruktion ist ein Verfahren, das einen nichtdeterministischen endlichen Automaten (NEA) in einen äquivalenten deterministischen endlichen Automaten (DEA) umwandelt.
Die Zustände des aus dem NEA abzuleitenden DEA sind Mengen von Zuständen des NEA. Ein Zustand vom DEA kodiert dabei all diejenigen Zustände, in denen sich der äquivalente nichtdeterministische Automat NEA zu einem bestimmten Zeitpunkt befinden könnte. Ein Zustandsübergang im DEA ist deterministisch, da sein Folgezustand aus der Menge aller möglichen Folgezustände besteht, in die ein NEA unter einer bestimmten Eingabe gelangen kann. Das Verfahren heißt Potenzmengenkonstruktion, weil die Zustände des konstruierten Automaten Mengen von Zuständen des Ausgangsautomaten sind und daher die konstruierte Zustandsmenge Teil der Potenzmenge der Zustandsmenge des Ausgangsautomaten ist.
Wir bertachten folgenden NEA als 5-Tupel (Quelle: https://de.wikipedia.org/wiki/Potenzmengenkonstruktion#Beispiele)
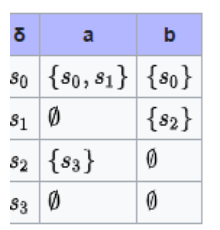
Q: S0,S1,S2,S3
S0∈Q
∑:a,b
F: S3
δ:Qx∑ ->Q
Die Übergangsfunktion des NEA lässt sich durch folgenden Graph beschreiben:
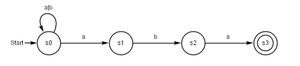
Nach obiger Konstruktion ergeben sich die Zustandsmenge Q′={S0′,S1′,S2′,S3′} und die Übertragungsfunktion δ′ des äquivalenten deterministischen Automaten wie folgt:
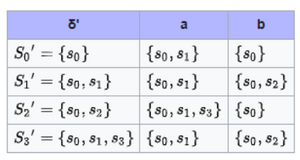
Neue Finalzustände sind die Zustände, die den Finalzustand des ursprünglichen NEA enthalten. Hier also S3′, da S3′ s3 enthält. Möglich ist, dass der abgeleitete DEA mehr Finalzustände besitzt als der zugrundeliegende NEA, da alle neuen Zustandsmengen die einen alten Finalzustände enthalten nun Endzustände sind. Insgesamt ergibt sich der deterministische Automat , der folgende graphische Darstellung besitzt:
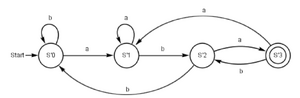
ε-NEA
ε-NEAs sind ein nützliches Werkzeug in der Theorie formaler Sprachen und Automatentheorie. Sie bieten Flexibilität und können in vielen Fällen den Design- und Analyseprozess vereinfachen, da Sie es ermöglichen, Zustände ohne das Verarbeiten eines Symbols zu wechseln. Das kann in manchen Situationen die Konstruktion eines Automaten erleichtern. In manchen Fällen kann ein ε-NEA eine kompaktere und klarere Darstellung eines Problems oder einer Sprache bieten als ein NEA oder DEA.
Um die Darstellung von endlichen Automaten zu vereinfachen, können Zustandsübergänge ohne Einlesen eines Zeichens ausgelöst werden. Diese Zustandsübergänge bezeichnet man als Epsilon-Übergänge. Für jeden nichtdeterministischen endlichen Automaten mit Epsilon-Übergängen gibt es einen nichtdeterministischen endlichen Automaten ohne Epsilon-Übergänge, der dieselbe Sprache erkennt, und umgekehrt. Die beiden Maschinenmodelle sind also äquivalent. Genau wie der normale nichtdeterministische endliche Automat erkennt ein nichtdeterministischer endlicher Automat mit Epsilon-Übergängen ein Wort w, wenn es in seinem Zustandsgraphen einen Pfad vom Startzustand zu einem Endzustand gibt.
Umwandlung ε-NEA zu NEA
Jeder ε-NEA lässt sich in einen NEA ohne ε-Übergänge umwandeln. Hierfür entfernt man die ε-Übergänge und betrachtet die Zustandsmengen, die von den Zuständen Q inklusive ε-Übergänge erreicht werden können. Für diese resultierenden Zustandsmengen wird analog zum Verfahren der Potenzmengenkonstruktion ein NEA ohne ε-Übergänge abgeleitet.
Beispiel
Das folgende Diagramm beschreibt einen NEA mit ε-Übergängen. Dieser Automat lässt sich als 5-Tupel beschreiben (Quelle: https://hwlang.de/theor/index.htm):
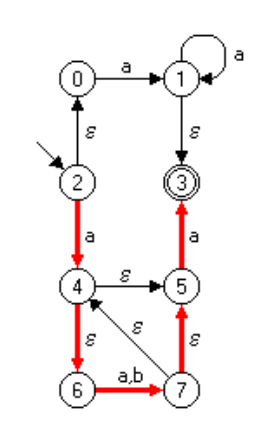
Q: 0-7
S∈2
∑:a,b,ε
F: 3
δ:Qx∑ ->Q
Er wird in der Folge in einen NEA ohne ε-Übergänge umgewandelt.