Rekursion: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „== Einführung == '''Rekursion''' stammt aus dem Lateinischen und bedeutet "das Zurücklaufen" (Duden). Die Rekursion ist eine sich selbst aufrufende Funktion. In der Java Programmierung nennt man Funktionen Methoden. In diesem Kontext handelt es sich also um selbstaufrufende Methoden. Die Rekursion ist ein Werkzeug, um komplexe Algorithmen zu entwickeln. Jeder Algorithmus, der sich mit einer Schleife abbilden lässt, lässt sich auch mit Rekursion abbild…“ |
Thomas (Diskussion | Beiträge) |
||
| (9 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== Einführung == | == Einführung == | ||
'''Rekursion''' stammt aus dem Lateinischen und bedeutet "das Zurücklaufen" (Duden). Die Rekursion ist eine sich selbst aufrufende Funktion. In der Java Programmierung nennt man Funktionen Methoden. In diesem Kontext handelt es sich also um selbstaufrufende Methoden. Die Rekursion ist ein Werkzeug, um komplexe Algorithmen zu entwickeln. Jeder Algorithmus, der sich mit einer Schleife abbilden lässt, lässt sich auch mit Rekursion abbilden, aber nicht umgekehrt. | '''Rekursion''' stammt aus dem Lateinischen und bedeutet "das Zurücklaufen" (Duden). Die Rekursion ist eine sich selbst aufrufende Funktion. In der [[Java]] Programmierung nennt man Funktionen [[Methode|Methoden]]. In diesem Kontext handelt es sich also um selbstaufrufende [[Methode|Methoden]]. Die Rekursion ist ein Werkzeug, um komplexe [[Algorithmus|Algorithmen]] zu entwickeln. Jeder [[Algorithmus]], der sich mit einer [[Schleife]] abbilden lässt, lässt sich auch mit Rekursion abbilden, aber nicht umgekehrt. | ||
Wichtig bei der rekursiven Programmierung ist die Definition einer Abbruchbedingung in der sich selbstaufrufenden Funktion. Diese Abbruchbedingung wird auch '''Rekursionsanker''' genannt. Ohne Abbruchbedingung würde sich das rekursive Programm theoretisch unendlich oft selbst aufrufen. | Wichtig bei der rekursiven Programmierung ist die Definition einer Abbruchbedingung in der sich selbstaufrufenden Funktion. Diese Abbruchbedingung wird auch '''Rekursionsanker''' genannt. Ohne Abbruchbedingung würde sich das rekursive Programm theoretisch unendlich oft selbst aufrufen. | ||
Rekursion stellt für viele Programmiereinsteiger am Anfang eine Herausforderung dar. Dennoch ist es wichtig, die Rekursion zu verstehen und auch anwenden zu können, da man mit ihrer Hilfe einige Problemfälle sehr elegant lösen kann. Dies ist z.B. beim Quicksort der Fall. | Rekursion stellt für viele Programmiereinsteiger am Anfang eine Herausforderung dar. Dennoch ist es wichtig, die Rekursion zu verstehen und auch anwenden zu können, da man mit ihrer Hilfe einige Problemfälle sehr elegant lösen kann. Dies ist z.B. beim [[Quicksort]] der Fall. | ||
<html> | |||
<iframe width="280" height="157.5" src="https://www.youtube.com/embed/_Aj8jvyjT8I?si=zVKexiyr1dAXgLZm" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" referrerpolicy="strict-origin-when-cross-origin" allowfullscreen></iframe> | |||
</html> | |||
== Beispiel == | == Beispiel == | ||
[[Datei:Rekursion Verschachtelung.png|mini|Verschachtelte Methodenaufrufe einer Rekursion ]] | |||
Ein Beispiel für die Verwendung einer rekursiven Programmierung ist die Berechnung der Fakultät einer Zahl. Die Fakultät ist das Produkt aller ganzen Zahlen von 1 bis zu dieser Zahl. Die Fakultät von 4 ist also: | Ein Beispiel für die Verwendung einer rekursiven Programmierung ist die Berechnung der Fakultät einer Zahl. Die Fakultät ist das Produkt aller ganzen Zahlen von 1 bis zu dieser Zahl. Die Fakultät von 4 ist also: | ||
:<math>1 \cdot 2 \cdot 3 \cdot 4 = 24</math> | :<math>1 \cdot 2 \cdot 3 \cdot 4 = 24</math> | ||
Der rekursive Algorithmus lässt sich wie folgt beschreiben: | Der rekursive [[Algorithmus]] lässt sich wie folgt beschreiben: | ||
* Will man die Fakultät von 4 berechnen, so muss man zunächst die Fakultät von 3 berechnen und das Ergebnis mit 4 multiplizieren. | * Will man die Fakultät von 4 berechnen, so muss man zunächst die Fakultät von 3 berechnen und das Ergebnis mit 4 multiplizieren. | ||
| Zeile 20: | Zeile 25: | ||
Die Berechnung im Detail: | Die Berechnung im Detail: | ||
* Die Fakultät von 1 ist also <math>1 \ | * Die Fakultät von 1 ist also <math>1 \cdot 1 = 1</math> | ||
* Die Fakultät von 2 ist also <math>1 \ | * Die Fakultät von 2 ist also <math>1 \cdot 1 \cdot 2 = 2</math> | ||
* Die Fakultät von 3 ist also <math>1 \ | * Die Fakultät von 3 ist also <math>1 \cdot 1 \cdot 2 \cdot 3 = 6</math> | ||
* Die Fakultät von 4 ist also <math>1 \ | * Die Fakultät von 4 ist also <math>1 \cdot 1 \cdot 2 \cdot 3 \cdot 4 = 24</math> | ||
In Java kann man die Fakultät folgendermaßen implementieren: | In Java kann man die Fakultät folgendermaßen implementieren: | ||
| Zeile 42: | Zeile 47: | ||
== Veranschaulichung == | == Veranschaulichung == | ||
Veranschaulichen lässt sich die Rekursion am Beispiel der Fakultät auch an Hand der folgenden Darstellung. Ruft man die Methode <code>fakultät(4)</code> auf, so wird als Eingabeparameter n=4 übergeben. Dieser Aufruf ist Aufruf Nummer 1. Es folgen drei weitere Aufrufe der Methode <code>fakultät(n)</code>, um die Fakultät vom Wert 4 zu berechnen. Im vierten und letzten Aufruf hat die Variable n den Wert 1 angenommen. Die Abbruchbedingung ist erfüllt. Nun werden die Methodenaufrufe - symbolisiert durch die Pfeile - nacheinander abgearbeitet. Durch dieses nachträgliche Abarbeiten, wird die latinische Bedeutung des Wortes Rekursion ersichtlich: recursio = das Zurücklaufen. | [[Datei:Rekursion BlueJ.png|mini|Veranschaulichung einer Rekursion mit dem Debugger]] | ||
Veranschaulichen lässt sich die Rekursion am Beispiel der [[Fakultät]] auch an Hand der folgenden Darstellung. Ruft man die [[Methode]] <code>fakultät(4)</code> auf, so wird als Eingabeparameter n=4 übergeben. Dieser Aufruf ist Aufruf Nummer 1. Es folgen drei weitere Aufrufe der [[Methode]] <code>fakultät(n)</code>, um die Fakultät vom Wert 4 zu berechnen. Im vierten und letzten Aufruf hat die [[Variable (Informatik)|Variable]] n den Wert 1 angenommen. Die Abbruchbedingung ist erfüllt. Nun werden die Methodenaufrufe - symbolisiert durch die Pfeile - nacheinander abgearbeitet. Durch dieses nachträgliche Abarbeiten, wird die latinische Bedeutung des Wortes Rekursion ersichtlich: recursio = das Zurücklaufen. Die Reihenfolge kann in [[BlueJ]] auch anhand der Call Sequenz im [[Debugger]] nachvollzogen werden. | |||
Die Reihenfolge kann in BlueJ auch anhand der Call Sequenz im Debugger nachvollzogen werden. | |||
[[Kategorie:Programmierung]] | [[Kategorie:Programmierung]] | ||
[[Kategorie:FI_I_SDM]] | [[Kategorie:FI_I_SDM]] | ||
[[Kategorie:AHR_I_Informatik_LK]] | [[Kategorie:AHR_I_Informatik_LK]] | ||
[[Kategorie:FI_I_TP1]] | |||
Aktuelle Version vom 29. September 2025, 13:55 Uhr
Einführung
Rekursion stammt aus dem Lateinischen und bedeutet "das Zurücklaufen" (Duden). Die Rekursion ist eine sich selbst aufrufende Funktion. In der Java Programmierung nennt man Funktionen Methoden. In diesem Kontext handelt es sich also um selbstaufrufende Methoden. Die Rekursion ist ein Werkzeug, um komplexe Algorithmen zu entwickeln. Jeder Algorithmus, der sich mit einer Schleife abbilden lässt, lässt sich auch mit Rekursion abbilden, aber nicht umgekehrt.
Wichtig bei der rekursiven Programmierung ist die Definition einer Abbruchbedingung in der sich selbstaufrufenden Funktion. Diese Abbruchbedingung wird auch Rekursionsanker genannt. Ohne Abbruchbedingung würde sich das rekursive Programm theoretisch unendlich oft selbst aufrufen.
Rekursion stellt für viele Programmiereinsteiger am Anfang eine Herausforderung dar. Dennoch ist es wichtig, die Rekursion zu verstehen und auch anwenden zu können, da man mit ihrer Hilfe einige Problemfälle sehr elegant lösen kann. Dies ist z.B. beim Quicksort der Fall.
Beispiel
Ein Beispiel für die Verwendung einer rekursiven Programmierung ist die Berechnung der Fakultät einer Zahl. Die Fakultät ist das Produkt aller ganzen Zahlen von 1 bis zu dieser Zahl. Die Fakultät von 4 ist also:
- [math]\displaystyle{ 1 \cdot 2 \cdot 3 \cdot 4 = 24 }[/math]
Der rekursive Algorithmus lässt sich wie folgt beschreiben:
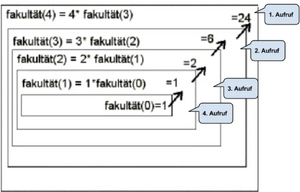
- Will man die Fakultät von 4 berechnen, so muss man zunächst die Fakultät von 3 berechnen und das Ergebnis mit 4 multiplizieren.
- Will man die Fakultät von 3 berechnen, so muss man zunächst die Fakultät von 2 berechnen und das Ergebnis mit 3 multiplizieren.
- Will man die Fakultät von 2 berechnen, so muss man zunächst die Fakultät von 1 berechnen und das Ergebnis mit 2 multiplizieren.
- Will man die Fakultät von 1 berechnen, so muss man zunächst die Fakultät von 0 berechnen und das Ergebnis mit 1 multiplizieren.
- Die Fakultät von 0 ist nach Definition 1.
Die Berechnung im Detail:
- Die Fakultät von 1 ist also [math]\displaystyle{ 1 \cdot 1 = 1 }[/math]
- Die Fakultät von 2 ist also [math]\displaystyle{ 1 \cdot 1 \cdot 2 = 2 }[/math]
- Die Fakultät von 3 ist also [math]\displaystyle{ 1 \cdot 1 \cdot 2 \cdot 3 = 6 }[/math]
- Die Fakultät von 4 ist also [math]\displaystyle{ 1 \cdot 1 \cdot 2 \cdot 3 \cdot 4 = 24 }[/math]
In Java kann man die Fakultät folgendermaßen implementieren:
public int fakultät(int n) {
if (n > 1) {
// bevor n mit der Rückgabe von fakultät multipliziert wird,
// wird fakultät erneut aufgerufen
// Solange bis n <= 1; Dies ist die Abbruchbedingung
return (n * fakultät(n - 1));
} else {
// Fakultät von 0 und 1 liefert immer 1
return (1);
}
}
Veranschaulichung
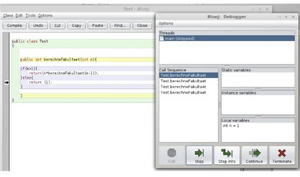
Veranschaulichen lässt sich die Rekursion am Beispiel der Fakultät auch an Hand der folgenden Darstellung. Ruft man die Methode fakultät(4) auf, so wird als Eingabeparameter n=4 übergeben. Dieser Aufruf ist Aufruf Nummer 1. Es folgen drei weitere Aufrufe der Methode fakultät(n), um die Fakultät vom Wert 4 zu berechnen. Im vierten und letzten Aufruf hat die Variable n den Wert 1 angenommen. Die Abbruchbedingung ist erfüllt. Nun werden die Methodenaufrufe - symbolisiert durch die Pfeile - nacheinander abgearbeitet. Durch dieses nachträgliche Abarbeiten, wird die latinische Bedeutung des Wortes Rekursion ersichtlich: recursio = das Zurücklaufen. Die Reihenfolge kann in BlueJ auch anhand der Call Sequenz im Debugger nachvollzogen werden.